高二数学导数定义高考练习

高考导数定义（本人针对新课表1-2和2-2做里系列类似资料，后续资料如果需要联系）

1.函数在处的导数等于　　 　　　　　　　　　　　　　　　　（　　 ）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

解析：函数的导数为，所以，故选D.

2.在函数的图象上，其切线的倾斜角小于的点中，坐标为整数的点的个数是 （　　 ）

　　　 　 A．3　　　　　　　　　　 B．2　　　　　　　　　　　　C．1　　　　　　　　　　　　D．0

解析：根据导数定义求出函数的导数为，依题意得，即，故整数x有三个，坐标为整数的点也有3个.故选A.

3.（06全国文2）过点（-1，0）作抛物线的切线，则其中一条切线为（　　）

（A） （B） （C） （D）

　 解析：设为作抛物线上一点，则在该点处切线的斜率为

　　　于是过点的抛物线的切线的方程为，又，

又，

解之得，于是

则：过（0，1）的切线方程为，即

过（-2，-3）的切线方程为，即

　　 故选D

 讲评：本题考查利用导数的几何意义求抛物线的切线方程，注意点（-1，0）不在抛物线上.

4．（2006年安徽卷）若曲线的一条切线与直线垂直，则的方程为（　 ）

A．　 B．　C．　　D．

解：与直线垂直的直线为，即在某一点的导数为4而，所以在(1，1)处导数为4，此点的切线为，故选A

5.曲线和在它们的交点处的两条切线与轴所围成的三角形的面积是___________.

解析：两曲线方程联立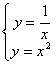得，解得，

　　

　　 　　

　　 　 

　　

6.

函数y＝ax²＋1的图象与直线y＝x相切，则a＝( 　　)

(A) 　　(B)　　 (C) 　　 (D)1

解：方法（一）利用切线的性质由题意,得有两个等实根,得a=,选(B)

　方法（二）利用导数定义可得，切点在直线y＝x设切点为（x,x）,根据切点在y＝ax²＋1和切点的导数为切线的斜率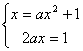得 可得.

7.

曲线y=x³在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为__________。

解析：∵=3x²,∵在(1,1)处切线为y-1=3(x-1),令y=0,得切线与x轴交点(),切线与直线x=2交于(2,4),∴曲线处的切线与x轴、直线所围成的三角形的面积为S=..

8.曲线处的切线与x轴、直线所围成的三角形的面积为=　　　　  .

解析：∵=3x²,∵在(a,a³)处切线为y-a³=3a²(x-a),令y=0,得切线与x轴交点(),切线与直线x=a交于(a,a³),∴曲线处的切线与x轴、直线所围成的三角形的面积为S=,令S=,解得a=±1.

9.过点P（－1，2）且与曲线y=3x²-4x+2在点M（1，1）处的切线平行的直线方程是__________.

解析：y=3x²-4x+2的导数为，故过点M（1，1）处的切线的斜率为2，又过点P（－1，2），可以求得直线方程为

10

曲线在点（1，1）处的切线方程为____________．

　 解析：因为（1，1）在曲线上，所以可以求得，故切线的斜率为，求得切线的方程为

11.曲线在点（1,3）处的切线方程是_________________．

　 解析：因为（1，3）在曲线上，所以可以求得，故切线的斜率为4，求得切线的方程为

12.

　　　 已知直线为曲线在点（1，0）处的切线，为该曲线的另一条切线，且

（Ⅰ）求直线的方程；

（Ⅱ）求由直线、和轴所围成的三角形的面积..

分析：根据点（1，0）在直线上，利用导数求得直线的方程，根据求出的斜率，从而求得的方程.进而求得三角形的面积.

解：y′=2x+1.

直线l₁的方程为y=3x－3.

设直线l₂过曲线y=x²+x－2上 的点B（b, b²+b－2）,则l₂的方程为y=(2b+1)x－b²－2

因为l₁⊥l₂，则有2b+1=

所以直线l₂的方程为

（II）解方程组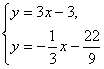　得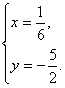

所以直线l₁和l₂的交点的坐标为

l₁、l₂与x轴交点的坐标分别为（1，0）、.

所以所求三角形的面积

评注：本题考查了利用导数求两种切线的方法，在求切线是一定要注意点是否在曲线上.如果点在曲线上直接利用该点导数，求出直线的方程；如果点不在直线上，首先求出切点坐标，然后进行求解.

 已知抛物线C₁：y=x²+2x和C：y=－x²+a，如果直线l同时是C₁和C₂的切线，称l是C₁和C₂的公切线，公切线上两个切点之间的线段，称为公切线段.

　 （Ⅰ）a取什么值时，C₁和C₂有且仅有一条公切线？写出此公切线的方程；

　 （Ⅱ）若C₁和C₂有两条公切线，证明相应的两条公切线段互相平分.

　分析：根据导数可以求得两切线的方程，有且仅有一条公切线即两方程为同一个方程，可以求a的值；若证明两公切线平分，即证明中点相同即可.

（Ⅰ）解：函数y=x²+2x的导数y′=2x+2,曲线C₁在点P（x₁,x+2x₁）的切线方程是：

y－(x+2x₁)=(2x₁+2)(x－x₁),即 y=(2x₁+2)x－x　①

函数y=－x²+a的导数y′=－2x, 曲线C₂ 在点Q（x₂,－x+a）的切线方程是

即y－(－x+a)=－2x₂(x－x₂).　 y=－2x₂x+x+a .　　 ②

如果直线l是过P和Q的公切线，则①式和②式都是l的方程，

　　　　x₁+1=－x₂

所以　　　　　　　　 

　　  　－ x=x+a.

消去x₂得方程　2x+2x₂+1+a=0.

若判别式△=4－4×2（1+a）=0时，即a=－时解得x₁=－，此时点P与Q重合.

即当a=－时C₁和C₂有且仅有一条公切线，由①得公切线方程为　y=x－ .

　 （Ⅱ）证明：由（Ⅰ）可知.当a<－时C₁和C₂有两条公切线

设一条公切线上切点为：P（x₁,y₁）, 　 Q（x₂ , y₂ ）.

其中P在C₁上，Q在C₂上，则有

x₁+x₂=－1,

y₁+y₂=x+2x₁+(－x+a)= x+2x₁－(x₁+1)²+a=－1+a .

线段PQ的中点为

同理，另一条公切线段P′Q′的中点也是

所以公切线段PQ和P′Q′互相平分.　

讲评：本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力