高二数学上期立体几何测试卷

高二数学上期立体几何测试卷

　　 时量：90分钟　　 满分：100分

班级　　　　　学号　　　　　　姓名　　　　　　

 

一、选择题（4’×10=40’）

1．一条直线与一个平面所成的角等于，另一直线与这个平面所成的角是. 则这两条直

　 线的位置关系　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．必定相交　 　　　 B．平行　　　　　　　　C．必定异面　　　　　D．不可能平行

2．下列说法正确的是　　　。

　　　 A．直线a平行于平面M，则a平行于M内的任意一条直线

　　　 B．直线a与平面M相交，则a不平行于M内的任意一条直线

　　　 C．直线a不垂直于平面M，则a不垂直于M内的任意一条直线

　　　 D．直线a不垂直于平面M，则过a的平面不垂直于M

3．设P是平面α外一点，且P到平面α内的四边形的四条边的距离都相等，则四边形是　　　。

　　　 A．梯形 　 B．圆外切四边形　　　　 C．圆内接四边形 　 D．任意四边形

4．平面α与正四棱柱的四条侧棱AA₁、BB₁、CC₁、DD₁分别交于E、F、G、H.若AE=3，BF=4，CG=5，则DH等于　　  。

A．6　　　 　　　　  B．5　 　　　　　　C．4　　 　　　　　　 D．3

5．二面角α—EF—β是直二面角，C∈EF，AC α，BCβ,∠ACF=30°,∠ACB=60°，则cos∠BCF等于　　　。

A．　　　　　　　　　 B． 　　　　　　　　　C．　　　　　　　　　　D．

6．把∠A=60°，边长为a的菱形ABCD沿对角线BD折成60°的二面角，则AC与BD的距离为（　　）

A.a　　　　　　 B.a　　　 C.a　　　　　　　　　　　　　　　 D.a

7．＝＝4，〈，〉＝60°，则－＝　　　。

　　 A.　4　　　　  B.　8　　　 C.　37　　　　 D.　13

8．三棱柱中，M、N分别是、的中点，设，，，则等于　　 。

　（A）　 （B）　 （C）　 （D）

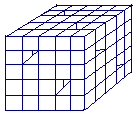9．如图，棱长为5的正方体无论从哪一个面看，都有两个直通的

　 边长为1的正方形孔，则这个有孔正方体的表面积（含孔内各

　 面）是　　 。

　　　 A．258　　B．234 　　C．222　　　　　D．210

10．在半径为的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是:

　　　 A． 　　　　B．　　　　　C．　　　　　　　D．

　　

将选择题答案填入下表（3’×12=36’）

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题（4’×5=20’）

11．边长为2的正方形ABCD在平面α内的射影是EFCD，如果AB与平面α的距离为，则AC与平面α所成角的大小是　　　　　　　　 　　　。

12．球的半径为8，经过球面上一点作一个平面，使它与经过这点的半径成45°角，则这个平面截球的截面面积为　　　　 　　　　。

13．已知AB是异面直线a、b的公垂线段，AB=2，且a与b成30°角，在直线a上取AP=4，则点P到直线b的距离为　　　　　　　　　　　 。

14．一个凸多面体的棱数为30，面数为12，则它的各面多边形内角总和为　　　　 　　　　。

15．已知a、b是直线，、、是平面，给出下列命题：

　 ①若∥，a，则a∥　　 ②若a、b与所成角相等，则a∥b

③若⊥、⊥，则∥　　④若a⊥, a⊥，则∥

 其中正确的命题的序号是________________。

三、解答题（40分）

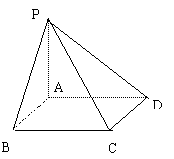
16．（8分）在△ABC所在平面外有点S，斜线SA⊥AC，SB⊥BC，且斜线SA、SB与平面ABC所成角相等.（I）求证：AC=BC；

　 （II）又设点S到平面ABC的距离为4cm，AC⊥BC且AB=6cm，求S与AB的距离.

　

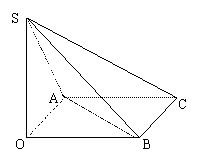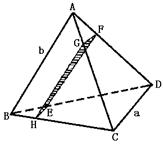
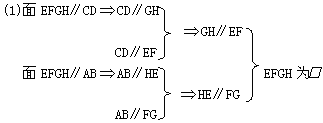
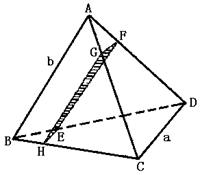17．（10分）平面EFGH分别平行空间四边形ABCD中的CD与AB且交BD、AD、AC、BC于E、F、G、H.CD=a，AB=b，CD⊥AB．

　 （I）求证EFGH为矩形；

　 （II）点E在什么位置，S_EFGH最大?

18．(12分）如图：直三棱柱，底面三角形ABC中，，，棱，M、N分别为A₁B₁、AB的中点

　①求证：平面A₁NC∥平面BMC₁；　②求异面直线A₁C与C₁N所成角的大小；

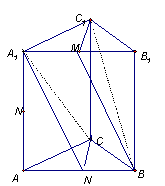③求直线A₁N与平面ACC₁A₁所成角的大小。

19．（10分）如图，四边形ABCD是矩形，PA⊥平面ABCD，其中AB=3，PA=4，若在线段PD上存在点E使得BE⊥CE，求线段AD的取值范围，并求当线段PD上有且只有一个点E使得BE⊥CE时，二面角E—BC—A正切值的大小.

　　　

岳阳市一中2007年上期立体几何测试卷答案

一、将选择题答案（3’×12=36’）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	B	B	C	D	A	A	D	B	B

二、填空题答案（4’×5=20’）

11． ； 12．  ；13． 14． ； 15．（1）（4）

三、解答题（10’×4=40’）

16．（1）证明：过S作SO⊥面ABC于O

　

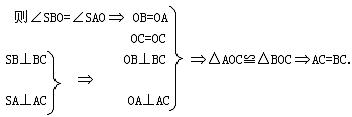
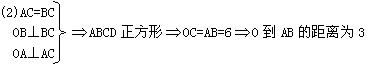
17．解：

又∵AB⊥CDEF⊥FGEFGH为矩形.

　 （2）AG=x，AC=m，

  ，GH=x

 　GF=（m－x）

　　　　 S_EFGH=GH·GF=x·（m－x）

　　　　 =（mx－x²）= （－x²+mx－+）=［－（x－）²+］

　　　　 当x=时，S_EFGH最大=

18、建系：A（1,0，0），B（0,1，0），C（0，0,0）

　　　　　，，，，

（1），，，

，，，

，平面A₁NC∥平面BMC₁

（2），

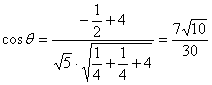
异面直线A₁C与C₁N所成角的大小为

（3）平面ACC₁A₁的法向量为，

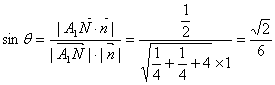
直线A₁N与平面ACC₁A₁所成角的大小为

19．若以BC为直径的球面与线段PD有交点E，由于点E与BC确定的平面与球的截面是一个大圆，则必有BE⊥CE，因此问题转化为以BC为直径的球与线段PD有交点。

　　　 设BC的中点为O（即球心），再取AD的中点M，易知OM⊥平面PAD，作ME⊥PD交PD于点E，连结OE，则OE⊥PD，所以OE即为点O到直线PD的距离，又因为OD＞OC，OP＞OA＞OB，点P，D在球O外，所以要使以BC为直径的球与线段PD有交点，只要使OE≤OC（设OC=OB=R）即可。

　　　 由于△DEM∽△DAP，可求得ME=  ， 所以OE²=9+ 令OE²≤R²，

　　　 即9+ ≤R² ，解之得R≥2；所以AD=2R≥4，所以AD的取值范围[ 4，+∞，

　　　 当且仅当AD= 4时，点E在线段PD上惟一存在，此时易求得二面角E—BC—A的平面角正切值为。