第二学期期中考试
高二数学试卷
本试卷满分150分 考试时间120分钟
第一卷
一、选择题：(本大题共10小题，每小题5分，共50分．在每小题中只有一项是符合题目要求的．)
1．化简
(
)
A．
B．
C．
D．
2．
（ ）
A 1 B 
C -
D -1
3．“函数
在一点的导数值为在这点取极值”的（ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
4． 复数
的共轭复数是(
)
A．
B．
C．
D．
5． 11. 有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线
平面
，直线
平面，直线
∥平面，则直线∥直线
”的结论显然是错误的，这是因为
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
6.一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是
( )
(A)12 (B) 13 (C)14 (D)15
7． 曲线3x2－y＋6=0在x=－
处的切线的倾斜角是
A.
B.－
C.
π
D.－π
8. 给出下面的程序框图，那么，输出的数是（ ）
 |
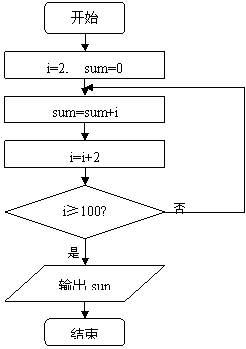
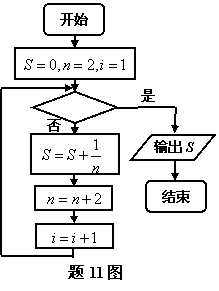A．2450 B.
9.已知
，猜想
的表达式为
A.
B.
C.
D.
10. 已知
是R上的单调增函数，则的取值范围是 （ ）
A.
B. 
C. 
D. 
二．填空题：(本大题共4小题，每小题5分，共20分)
11. 右图给出的是计算
的值的一个
程序框图,其中判断框内应填入的条件是__________
12．设
，则
的实部是________，虚部是________。
13．
在x = 2处有极大值，则常数c 的值为_________；
14．类比平面几何中的勾股定理：若直角三角形ABC中的两边AB、AC互相垂直，则三角形三边长之间满足关系：
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则三棱锥的侧面积与底面积之间满足的关系为
.
三．解答题：（本题共6小题，共80分）
15.求证：(1)
;
(2) 
+
>2
+
。
16．（12分）已知复数
.当实数
取什么值时，复数
是
（1） 零；
（2） 虚数；
（3） 纯虚数；
（4） 复平面内第二、四象限角平分线上的点对应的复数。
17．（14分）设
是
的等差中项，
是
的等比中项，求证
18．（14分）已知是复数，
，
均为实数（为虚数单位），且复数
在复平面上对应的点在第一象限，求实数的取值范围。
19（14分）若函数
在区间（1，4）内为减函数，在区间（6，+∞）上为增函数，试求实数的取值范围。
20．（14分）已知函数
的图象在点
处的切线方程为
（1） 求函数
的解析式；
（2） 求函数
的单调区间。
第五中学2006-2007学年度第二学期期中考试
高二数学答案
(时间120分钟,满分150分.)
高二 班 学号 姓名 成绩
一、选择题(本大题共10小题，每小题5分，共50分)．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | B | B | A | C | C | A | B | D |
二.填空题(每题5分,共20分)
11． I>10
12． 
13． 6
14． 
三．解答题：（本题共6小题，共80分）
15（1） ∵
,
,
;将此三式相加得
2
,∴.
（2）要证原不等式成立，只需证（+）
>（2+），即证
。
∵上式显然成立, ∴原不等式成立.
16解：
17证明：
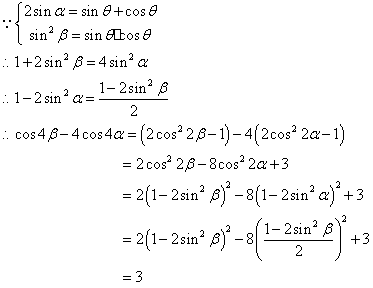
18 解：
设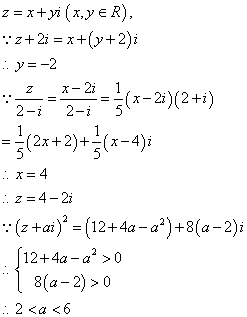
19解：
令
得
当
即
时
在
上是增函数，不合题意。
当
时，函数在
，
上是增函数，
在
上是减函数。
依题意有：
即
20解：（1）由函数的图象在点M
处的切线方程为 ，知
，即
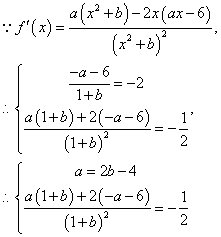
解得
所以所求的函数解析式是
（2）
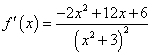
令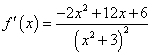=0
解得
当
或
时
；
当
时，
所以函数在
是增函数，
在
内是减函数。