高二数学下期中试卷

高二数学下期中试卷

班级：　　座号：　　姓名：

一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的）计48分.

1. 经过同一直线上的3个点的平面　　　　　　　　　　　　　　  ………(　 ）

 A.有且只有一个  B.有且只有3个　　 C.有无数多个　　  D.只有0个

2.若平面α∥平面β，直线m平面α，点A∈β，则在β内过点A的所有直线中(　)

（A）不一定存在和m平行的直线　（B）只有两条和m平行的直线

 （C）存在无数条和m平行的直线　　 （D）存在唯一一条和m平行的直线

3. 现在国际乒乓球赛的用球已由“小球”改为“大球”，“小球”的直径为38mm，“大球”的直径为40mm，则“小球”的表面积与“大球”的表面积之比　　　　……（　 ）

A .19³:20³B.19²:20² 　　 C.19:20　　　 D.:

4. 下列命题中正确的是　　 　　　　　　　　　　　　　　　　　　　　 ……（　 ）

A．垂直于同一直线的两条直线平行；B.若一条直线垂直于两条平行线中的一条，则它垂直于另一条；C.若一条直线与两条平行线中的一条相交，则它与另一条也相交；

D.一条直线至多与两条异面直线中的一条相交。

5.下列说法正确的是　 　　　　　　 　　　　　　　　　　　　　　　　　　……（　　）

　　　 A．直线a平行于平面M，则a平行于M内的任意一条直线

　　　 B．直线a与平面M相交，则a不平行于M内的任意一条直线

　　　 C．直线a不垂直于平面M，则a不垂直于M内的任意一条直线

　　　 D．直线a不垂直于平面M，则过a的平面不垂直于M

6.三棱锥成为正三棱锥的充分而不必要条件是 　　　　　　　　　　　  ……（　　）

　　　 A．各侧面与底面所成的角相等 B．各侧面是全等的等腰三角形

　　　 C．高通过底面外心，且底面是正三角形 D．四个面均为正三角形

7.二面角α—EF—β是直二面角C∈EF，ACα，BCβ,∠ACF=30°,∠ACB=60°，

则cos∠BCF等于　　　　　　　　　　　　　　　　　　　　　　　　　 ……(　　)

A．　　　　　 B．　　 C． 　　　D．

8.长方体的对角线长为2，则其全面积的最大值为　　　　 　　　　　　　  ……（　　）

　　　 A．　 　　B． 　　　C．4　　　 　　D．8

9.在北纬45°的纬度圈上有甲、乙两地，两地经度差为90°，则甲、乙两地最短距离为（设地球半径为R）　　　　　　　　　　　　　　　 　　　　　　……　(　　)

A. 　　　　 B. 　C. 　　　　　　　D.

10.给出下列命题：

①平行于三角形两边的平面平行于三角形的第三边；②垂直与三角形两边的直线垂直于三角形的第三边；③与三角形各顶点距离相等的平面平行于三角形所在平面；④钝角三角形在一个平面内的射影可以是锐角三角形。其中假命题的个数是（　）

A．一个　B．两个　　 C．三个 　 D．四个

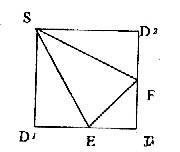
11.如图,E、F分别是正方形SD₁DD₂的边D₁D,DD₂的中点, 沿SE,SF,EF将其折成一个几何体,使D₁,D,D₂重合,记作D.则SD与平面DEF所成的角　　　　…… (　　)

Ａ. 60°　　 B.90° 　　C. 0°　　　 D. 度数无法确定。

12.平面α与正四棱柱的四条侧棱AA₁、BB₁、CC₁、DD₁分别交于E、F、G、H.若AE=3，BF=4，CG=5，则DH等于　　　 　　　　　　　　　　　　　　　　　　 ……（　　）

A．6　　　 B．5　　　 C．4　　　 D．3

二、填空题（本大题共4小题，每小题5分，共20分）

13. 长方体的长、宽、高分别为2，3，4，则它的对角线长为_________.

14.两个平行的平面之间的距离为12CM，一条直线和其中一个平面相交成60°角，则这条直线夹在这两个平面间的线段的长为_____________.

15.已知正三棱锥的高为4CM，底面边长为6CM，则它的斜高为____CM。

16.线段AB的端点到平面α的距离分别为3和7，则AB中点到平面α的距离为__________ 

三. 解答题(共82分)

17（15分）.如图，α∩β=AB,PC⊥α,PD⊥β,C、D是垂足。问：直线AB与CD位置有什么关系，证明你的结论。

18. (本小题15分)

如图：四边形ABCD在平面α内，且AB⊥AD，AB=AD=5，

∠ADC=135°，PB⊥α，PB=12，求点P到边CD的距离。

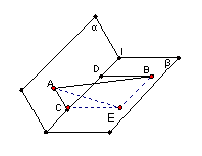
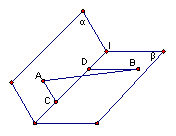19（15分）.已知二面角α-l-β的大小为120°，A∈α，B∈β，点A和B到棱l的距离AC和BD分别为2和4，且AB=10。求直线AB和棱l所成的角；

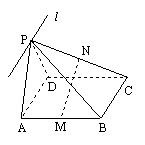
20.（16分）

 如图，P为□ABCD所在平面外一点，M、N分别是AB、PC的中点，平面PAD∩平面PBC=l。

（1） 求证：BC∥l　　

（2）问MN与平面PAD是否平行？并证明你的结论。

 

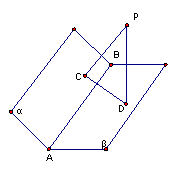
21.(2005福建高考题,每小题7分计21分)

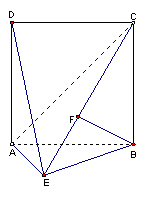如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE。

1）　求证：AE⊥平面BCE。

2）　求二面角B-AC-E的大小。

3）　求点D到平面ACE的距离。

榜头二中高二下期中数学试卷答案

一、　　　  选择题：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	C	D	B	B	B	D	D	D	B	A	B	C

二、填空题（本大题共4小题，每小题4分，共16分）

13. 。　　14. 。15. 5。　　　16. 5或2。

三. 解答题(本大题共6小题,总分48分)

17.证PC⊥AB、PD⊥AB可得AB⊥平面PCD，从而得出AB⊥CD

18.解：连接BD，PD

　　　　 因为　AB⊥AD，AB=AD=5，则∠ADB=45°，又∠ADC=135°

　　∴　∠BDC=90°，即　CD⊥BD 而BD是PD在平面ABCD上的射影，

　　　由三垂线定理知　PD⊥CD 即PD为P到CD的距离

∵　BD=　PB=12　　　　  ∴　PD=

19．证：作CE⊥l,且CE=DB，连结BE、AE。

　　　　可知∠ACE为二面角α-l-β的平面角，

AE=AC²+CE²-2AC·CE·cos120°=2.

由已知可证l⊥平面ACE，则BE⊥平面ACE，

在Rt△ABE中，sinABE=，∴∠ABE=arcsin

20. (1)先证BC∥平面PAD 　 (2)平行，取PD中点E，连结AE，证MN∥AE。

21.见下页