数学会考模拟试题（B）
一选择题
1．已知集合
，
，则
等于
A
B 
C 
D 
2．函数
的反函数是
A
B
C
D
3．已知等差数列
中，
，则
的值是
A
1
B
4．设函数的图象过点（1，2），则反函数的图象过点
A （1，2） B（-1，-2） C（-2，-1） D （2，1）
5．
是
的
A充分不必要条件 B必要不充分条件 C充分必要条件 D 既不充分也不必要条件
6．一条直线若同时平行于两个相交平面，则这条直线与这两个相交平面的位置关系是
A 异面 B相交 C平行 D平行或相交
7．点P在直线
上，O为原点，则OP的最小值为
A-2
B 
C 
D 
8．若向量a=1, b=2, c= a+ b且c⊥a，则向量a与b的夹角为
A
B 
C 
D 
9．若抛物线
的焦点与椭圆
的右焦点重合，则P的值为
A -2 B
10．不等式组
表示的平面区域是一个
A 三角形 B 梯形 C 矩形 D 菱形
11．已知正方体的外接球的体积是
，那么正方体的棱长等于
A B 
C 
D 
12．函数
在下列哪个区间是减函数
A
B
C
D
13．从4名男生和3名女生中选出3人，分别从事三项不同的工作，若这3人中至少有1名女生，则选派方案共有
A 108种 B 186 种 C 216种 D 270种
14．函数
对任意的实数t都有
则A 
B 
C 
D 
15．已知过点A（-2，m）和B（m,4）的直线与直线2x+y-1=0平行，则m的值为
A 0 B
16．双曲线
的渐近线方程
A 
B
C
D
17．在下列函数中，函数的图象关于y轴对称的是
A
B
C
D 
18．将的图象上的所有点的纵坐标不变，横坐标缩小到原来的一半，然后再将图象沿x轴负方向平移
个单位，则所得图象的解析式为
A 
B
C
D
19．设我方每枚地对空导弹独立地击中敌机的概率为
，如果要以99%的把握击中来犯敌机，则至少要同时发射导弹
A 2枚 B 3 枚 C 4枚 D 5枚
20.建造一个容积为8
，深为2
的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为
A 1700元 B 1720元 C 1740元 D 1760元
二：填空题
21．函数
的值域
22．不等式
的解集
23．抛物线
的准线方程是
24．在
的展开式中，含
项的系数为
三：解答题
25．在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD是正三角形，平面PAD 
底面ABCD
（1） 证明AB 平面PAD
（2） 求面PAD与面PDB所成的二面角的正切值
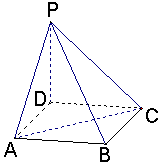如图ABCD是正方形，
面ABCD，PD=DC。
（1）求证：ACPB；
（2）求二面角
的大小；
（3）求AD与PB所成角的正切值。
26．设二次方程
有两根
和
，且满足
（1）
试用
表示
；
（2）
求证：
是等比数列；
（3）
当
时，求数列的通项公式。
27．已知椭圆
的长、短轴端点分别为A、B，从此椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点
，向量
与
是共线向量
（1）求椭圆的离心率；
（2）设Q是椭圆上任意一点，
分别是左、右焦点，求
的取值范围。
会考数学（B）卷答案
答题卡
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | A | B | D | B | C | B | C | D | A |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| D | C | B | A | B | C | C | B | B | D |
21． [-2,0]
22．
或
23．
24． 20
25．证明：（1）取AD的中点O，连接PO，
侧面PAD是正三角形，
POAD，
又面PAD面ABCD则POAB，又底面是正方形，所以PAAB，则AB面PAD
（2）
取PD的中点E连接AE、连接BE由（1）及三垂线定理知
为所求的二面角
在直角三角形AEB中，设AB=a，则
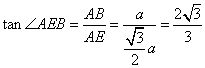
26．（1）解：根据韦达定理得
由得
故
（2）因为
所以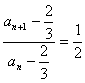
所以数列是等比数列
（3）
当的首项为
所以
所以：
27．解：
则
是共线向量，所以
所以b=c，
（2）设
所以
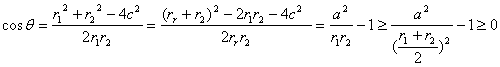
当且仅当
所以