会考模拟试题（A）
一选择题（共20个小题，每小题3分，共60分）
在每小题给出的四个备选答案中，只有一个是符合题目要求的，请把所选答案的字母按要求填在相应的位置上
1．
满足条件
的集合M的个数是
A 4 B
2．
的值为
A 
B 
C 
D 
3．
是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直的
A充分必要条件 B充分不必要条件 C必要不充分条件 D既不充分也不必要条件
4．设函数
的图象过点（，–3），则a的值
A 2 B –
5．直线a∥平面M, 直线a⊥直线b,则直线b与平面M的位置关系是
A 平行 B在面内 C 相交 D平行或相交或在面内
6．下列函数是奇函数的是
A
B
C 
D 
7．点（2，5）关于直线
的对称点的坐标是
A （6，3） B（-6，-3） C（3，6） D（-3，-6）
8．
值为
A
B 
C 
D 
9．已知等差数列
中，
，则该数列前9项和
等于
A
18 B
10．甲、乙两个人投篮，他们投进蓝的概率分别为
，现甲、乙两人各投篮1次
则两个人都投进的概率是
A
B
C 
D 
11．已知向量
和
的夹角为
，
，则
等于
A 1 B 
C 
D 2
12．两个球的体积之比是8：27，那么两个球的表面积之比为
A
2：3 B 4：
D
13．椭圆短轴长是2，长轴是短轴的2倍，则椭圆的中心到其准线的距离
A 
B
C 
D 
14．
已知圆的参数方程为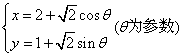
，那么该圆的普通方程是
A 
B 
C 
D 
15．函数
的最小正周期为
A
B
C
D 
16．双曲线
的离心率为
A
B 
C 
D
17．从数字1，2，3，4，5中任取3个，组成没有重复数字的三位数中是偶数的概率
A
B 
C 
D 
18．圆
截直线
所得弦长为8，则C的值为
A 10
B
19．6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有
A720 B
20．国庆期间，某商场为吸引顾客，实行“买100送20 ，连环送活动”即顾客购物每满100元，就可以获赠商场购物券20元，可以当作现金继续购物。如果你有680元现金，在活动期间到该商场购物，最多可以获赠购物券累计
A 120元 B 136元 C 140元 D160元
二填空题（共4小题，每小题3分，共12分）
21．直线
与直线
的夹角
22．直角坐标系xoy中若定点A（1，2）与动点（x,y）满足
，则点P的轨迹方程为
23．平面内三点A（0，-3），B（3，3），C（x，-1）若
∥
，则x的值
24．已知函数
，则
的定义域为
三：解答题（3小题，共28分）
25．如图ABCD是正方形，
面ABCD，PD=DC，E是PC的中点
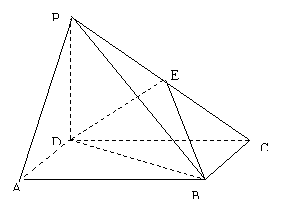（1）证明DE
面PBC
（2）求二面角
的大小
26．已知中心在原点的双曲线C的右焦点为（2，0），右顶点为
（1） 求双曲线C的方程
（2） 若直线
与双曲线C恒有两个不同的交点A和B，且
（其中O为原点）求 K的取值范围
27．已知函数
（1）判断
在
上的增减性，并证明你的结论
（2）解关于
的不等式
（3）若
在上恒成立，求
的取值范围
答案：会考数学（A）卷答案
答题卡
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | B | B | B | C | B | B | A | C | A |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| D | B | D | C | D | C | D | D | C | D |
21．
22．
23．1
24．{x
且
}
25．简证（1）因为PD面ABCD所以PDBC，又BCDC所以BC面PDC
所以BCDE，又PD
BC，PD=DC，E是PC的中点所以DEPC
所以DE面PBC
（2）
作EFPB于F，连DF，因为DE面PBC所以DFPB
所以
是二面角的平面角
设PD=DC=
又DE面PBC（已证）
DEEF所以
即
26．（1）解：设双曲线方程为
因为
（2）将代入双曲线中得
由直线与双曲线交与不同两点的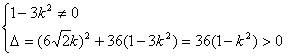
即
------------------------（1）
设
则
由
得
，令
解此不等式得
即
的
27．（1）证明设
在上为减函数
（2）
不等式即
即
1）
当
，不等式的解
2）
当
不等式的解
或
（舍）
（3）若在恒成立即
所以
因为
的最小值为4
所以
即
或