新课标高二数学同步测试(8)—(2-2第二章)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.已知α∩β=l,a![]() α、b
α、b![]() β,若a、b为异面直线,则 ( )
β,若a、b为异面直线,则 ( )
A. a、b都与l相交 B. a、b中至少一条与l相交
C. a、b中至多有一条与l相交 D. a、b都与l相交
2.已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的最大值为 ( )
的最大值为 ( )
A.1 B.![]() D.
D.![]()
3.某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
| 行业名称 | 计算机 | 机械 | 营销 | 物流 | 贸易 |
| 应聘人数 | 215830 | 200250 | 154676 | 74570 | 65280 |
| 行业名称 | 计算机 | 营销 | 机械 | 建筑 | 化工 |
| 招聘人数 | 124620 | 102935 | 89115 | 76516 | 70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是 ( )
A.计算机行业好于化工行业 B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张
4.已知![]() =2,关于p+q的取值范围的说法正确的是 ( )
=2,关于p+q的取值范围的说法正确的是 ( )
A.一定不大于2
B.一定不大于![]()
C.一定不小于![]() D.一定不小于2
D.一定不小于2
5.从棱长为![]() 的正方体的一个顶点A0出发,在体内沿一条直线进行到另一条上的点A1,使得A
的正方体的一个顶点A0出发,在体内沿一条直线进行到另一条上的点A1,使得A
A.18
B.
6.已知数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,设Sn=a1+a2+……+an,则下列结论正确的是 ( )
A.a100=-a S100=2b-a B.a100=-b S100=2b-a
C.a100=-b S100=b-a D.a100=-a S100=b-a
7.在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC
A.AB2+AC2+ AD2=BC2 +CD2 +BD2 B.![]()
C.![]() D.AB2×AC2×AD2=BC2 ×CD2 ×BD2
D.AB2×AC2×AD2=BC2 ×CD2 ×BD2
8.已知函数![]() ,则
,则![]() 、
、![]() 、
、![]() 与1的大小关系为 ( )
与1的大小关系为 ( )
A.没有一个小于1 B.至多有一个不小于1
C.都不小于1 D.至少有一个不小于1
9.已知直线l、m,平面α、β,且l⊥α,mβ,给出下列四个命题:
(1)若α∥β,则l⊥m;(2)若l⊥m,则α∥β;
(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β;
其中正确命题的个数是 ( )
A.1
B.
10.已知函数![]() ,对任意的两个不相等的实数
,对任意的两个不相等的实数![]() ,都有
,都有![]() 成立,且
成立,且![]() .则
.则![]() 的值是( )
的值是( )
A.0
B.
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.若函数![]() 其中
其中![]() ,
,![]() 是
是![]() 的小数点后第n为数字,例如
的小数点后第n为数字,例如![]() ,则
,则![]() (共2005个f)=
.
(共2005个f)=
.
12.已知结论 “若![]() ,且
,且![]() ,则
,则![]() ”,请猜想若
”,请猜想若![]() ,且
,且![]() ,则
,则![]() .
.
 13.数列的前几项为2,5,10,17,26,……,数列的通项公式为 .
13.数列的前几项为2,5,10,17,26,……,数列的通项公式为 .
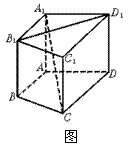
14.如图,在直四棱柱A1B
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知a,b,c是全不相等的正实数,求证![]() .
.
16.(12分)若![]() 、
、![]() ,
,![]()
![]()
(1)求证:![]() ;
;
(2)令![]() ,写出
,写出![]() 、
、![]() 、
、![]() 、
、![]() 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式![]() ;
;
(3)证明:存在不等于零的常数p,使![]() 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.
17.(12分)对于直线l:y=kx+1,是否存在这样的实数k,使得l与双曲线C:3x![]() -y
-y![]() =1的交点A、B关于直线y=ax(a为常数)对称?若存在,求出k的值;若不存在,请说明理由.
=1的交点A、B关于直线y=ax(a为常数)对称?若存在,求出k的值;若不存在,请说明理由.
18.(12分)由下列各式:
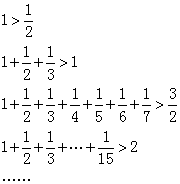
你能得出怎样的结论,并进行证明.
19.(14分)设二次函数f(x)=ax2+bx+c (a,b,c∈R,a≠0)满足条件:
①当x∈R时,f(x-4)=f(2-x),且f(x)≥x;②当x∈(0,2)时,f(x)≤![]()
③f(x)在R上的最小值为0.
求最大值m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
20.(14分)(反证法)对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点.如果函数
的不动点.如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立
成立
参考答案
一、
1.B;2.A;3.B;4.A;5.A;6.A;7.C;8.D;9.B;10.B;
二、
11.1;12.![]() ;13.
;13.![]() ;14.AC⊥BD;
;14.AC⊥BD;
三、
15.证法1:(分析法)
要证 ![]()
只需证明 ![]()
即证 ![]()
而事实上,由a,b,c是全不相等的正实数
∴ ![]()
∴ ![]()
∴ ![]() 得证.
得证.
证法2:(综合法)
∵ a,b,c全不相等
∴ ![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 全不相等.
全不相等.
∴ ![]()
三式相加得![]()
∴ ![]()
即 ![]() .
.
16.解:(1)采用反证法. 若![]() ,即
,即![]() , 解得
, 解得 ![]()
从而![]() 与题设
与题设![]() ,
,![]() 相矛盾,
相矛盾,
故![]() 成立.
成立.
(2) ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() .
.
(3)因为![]() 又
又![]() ,
,
所以![]() ,
,
因为上式是关于变量![]() 的恒等式,故可解得
的恒等式,故可解得![]() 、
、![]() .
.
17.证明:(反证法)假设存在实数k,使得A、B关于直线y=ax对称,设A(x1,y1)、B(x2,y2)则
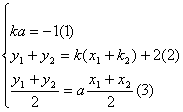
由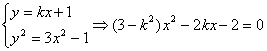 ④
④
由②、③有a(x1+x2)=k(x1+x2)+2 ⑤
由④知x1+x2=![]() 代入⑤整理得:ak=-3与①矛盾.
代入⑤整理得:ak=-3与①矛盾.
故不存在实数k,使得A、B关于直线y=ax对称.
18.分析:对所给各式进行比较观察,注意各不等式左边的最后一项的分母特点:1=21-1,3=22-1,7=23-1,15=24-1,…,一般的有2n-1,对应各式右端为一般也有![]() .
.
解:归纳得一般结论
![]()
证明:当n=1时,结论显然成立.
当n≥2时,
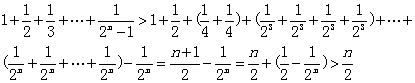
故结论得证.
![]()
![]() ,
,![]() .
.
故 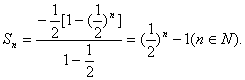
19.特殊—一般—特殊:其解法是先根据若干个特殊值,得到一般的结论,然后再用特殊值解决问题.
分析:本题先根据题设求出函数f(x)解析式,然后假设t存在,取x=1得t的范围,再令x=m求出m的取值范围,进而根据t的范围求出m的最大值.
解法一:∵f(x-4)=f(2-x),∴函数的图象关于x= -1对称
∴![]() 即b=
即b=
由③知当x= 1时,y=0,即ab+c=0;由①得 f(1)≥1,由②得 f(1)≤1.
∴f(1)=1,即a+b+c=1,又ab+c=0
∴a=![]() b=
b=![]() c=
c=![]() ,∴f(x)=
,∴f(x)=![]()
假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x
取x=1时,有f(t+1)≤1![]()
![]() (t+1)2+
(t+1)2+![]() (t+1)+
(t+1)+![]() ≤1
≤1![]() 4≤t≤0
4≤t≤0
对固定的t∈[-4,0],取x=m,有
f(tm)≤m![]()
![]() (t+m)2+
(t+m)2+![]() (t+m)+
(t+m)+![]() ≤m
≤m![]() m2(1t)m+(t2+2t+1)≤0
m2(1t)m+(t2+2t+1)≤0
![]()
![]() ≤m≤
≤m≤![]() ∴m≤
∴m≤![]() ≤
≤![]() =9
=9
当t=
-4时,对任意的x∈[1,9],恒有f(x4)x=![]() (x210x+9)=
(x210x+9)=![]() (x1)(x9)≤0
(x1)(x9)≤0
∴m的最大值为9.
解法二:∵f(x-4)=f(2-x),∴函数的图象关于x=-1对称
∴ ![]() b=
b=
由③知当x= 1时,y=0,即ab+c=0;由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即a+b+c=1,又ab+c=0
∴a=![]() b=
b=![]() c=
c=![]() ∴f(x)=
∴f(x)=![]() =
=![]() (x+1)2
(x+1)2
由f(x+t)=![]() (x+t+1)2≤x
在x∈[1,m]上恒成立
(x+t+1)2≤x
在x∈[1,m]上恒成立
∴4[f(x+t)-x]=x2+2(t-1)x+(t+1)2≤0当x∈[1,m]时,恒成立
令 x=1有t2+4t≤0![]() 4≤t≤0
4≤t≤0
令x=m有t2+2(m+1)t+(m-1)2≤0当t∈[-4,0]时,恒有解
令t=
4得,m210m+9≤0![]() 1≤m≤9
1≤m≤9
即当t=
4时,任取x∈[1,9]恒有f(x-4)-x=![]() (x210x+9)=
(x210x+9)=![]() (x1)(x9)≤0
(x1)(x9)≤0
∴ mmin=9
点评:本题属于存在性探索问题,处理这道题的方法就是通过x的特殊值得出t的大致范围,然后根据t的范围,再对x取特殊值,从而解决问题.
20.解:依题意有![]() ,化简为
,化简为 ![]() 由违达定理, 得
由违达定理, 得
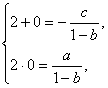 解得
解得 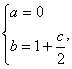 代入表达式
代入表达式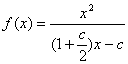 ,
,
由![]() 得
得 ![]() 不止有两个不动点,
不止有两个不动点,![]()
(2)由题设得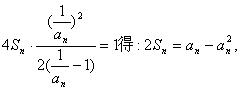 (*)
(*)
且![]() (**)
(**)
由(*)与(**)两式相减得:
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,由
,由![]() ,若
,若![]() 这与
这与![]() 矛盾,
矛盾,![]() ,即{
,即{![]() 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,![]() ;
;
(3)采用反证法,假设![]() 则由(1)知
则由(1)知![]()
![]() ,有
,有
![]() ,而当
,而当![]() 这与假设矛盾,故假设不成立,
这与假设矛盾,故假设不成立,![]() .
.
关于本例的第(3)题,我们还可给出直接证法,事实上:
由![]() 得
得![]() <0或
<0或![]()
![]() 结论成立;
结论成立;
若![]()
![]() ,此时
,此时![]() 从而
从而![]() 即数列{
即数列{![]() }在
}在![]() 时单调递减,由
时单调递减,由![]() ,可知
,可知![]() 上成立.
上成立.
比较上述两种证法,你能找出其中的异同吗? 数学解题后需要进行必要的反思, 学会反思才能长进.