高二数学同步测试9

新课标高二数学同步测试（9）—（2－2第三章）

说明：本试卷分第一卷和第二卷两部分，第一卷74分，第二卷76分，共150分；答题时间120分钟．

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

1．方程2z+z=2+6i的解的情况是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．没有解　　　　　　　 B．只有一解　　　　　　C．有两解　　　　　　D．多于两解

2．已知z=x＋yi(x，y∈R)，且 ，则z=　　　　　　　　 （　　）

　　　 A．2＋i　　 　　　　 B．1＋2i 　　　　　　 C．2＋i或1＋2i 　 D．无解

3．下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　A．任意两复数均不能比较大小；　　　　　B．复数z是实数的充要条件是z=；

　　　C．复数z是纯虚数的充要条件是z+=0；　　　D．i+1的共轭复数是i－1；

4．设，则集合中元素的个数是　　　（　  ）

　　　 A．1　　　　　　　　　B．2 　　　　　　　　 C．3　　　　　　　　　　D．无穷多个

5．使不等式m²－(m²－3m)i＜(m²－4m＋3)i＋10成立的实数m　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　B．0 　　　　　　　　C．3　　　　　  　 D．复数无法比较大小

6．设复数，则满足等式的复数对应的点的轨迹是　 （　　）

　　　A．圆　　 　　　　　　　B．椭圆　　　　　　　 C．双曲线　　　　 D．抛物线

7．若非零复数满足,则的值是　　　　　 （　　）

A．1　　　　 　　　　 B．　　 　　　　　　C．　　　　　　　 D．

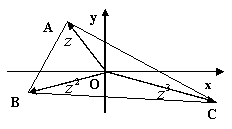
8．如图所示，复平面内有RtΔABC，其中∠BAC=90°，点A、B、C分别对应复数，且=2，则z=（　　）

　　　 A．　　　　　　B．

　　　 C．　　　　 D．

9．复数z＝a＋2ｉ，z＝－2＋ｉ，如果z< z，则实数a的取值范围是　　　　　（　　）

　　　 A．－1<a<1　 　　　　B．a>1 　　　　　　　　C．a>0　　　　　　　　D．a<－1或a>1

10．如果复数z满足z＋ｉ＋z－ｉ＝2，那么z＋ｉ＋1的最小值为______．

　　　 A．1　　　 　　　　　　B．　　　　  　 C．2　　　　 　　　　D．

二、填空题：请把答案填在题中横线上（每小题6分，共24分）．

11．已知关于x的实系数方程x²－2ax+a²－4a+4=0的两虚根为x₁、x₂，且x₁+x₂=3，则a的值为　　 　 　　　　 ．

12．已知(2x－1)+i=y－(3－y)i，其中x, y∈R，求x=　　　　  ， y=　　　　　  ．

13．i＋i²＋i³+……+i²⁰⁰⁵=　　　　　  ．

14．已知x、y、t∈R，t≠－1且 t≠0，求满足x＋yi=时，点(x, y)的轨迹方程

　　　　　　  ．

三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．

15．（12分）设z＝5，z＝2, z－＝，求的值．

16．（12分）当m为何实数时，复数z＝+(m²+3m－10)i；（1）是实数；（2）是虚数；（3）是纯虚数．

17．（12分）求同时满足下列条件的所有复数z:(1)是实数，且．(2)z的实部和虚部都是整数．

18．（12分）设复数z－i=1, 且z¹0, z¹2i. 又复数w使为实数，问复数w在复平面上所对应的点Z的集合是什么图形，并说明理由．

19．（14分）设虚数z₁,z₂，满足.

（1）若z₁,z₂又是一个实系数一元二次方程的两根，求z₁, z₂．

（2）若z₁=1+mi(i为虚数单位，m∈R), ,复数w=z₂+3,求w的取值范围．

20．（14分）已知：A、B是ABC的两个内角，，

其中、为相互垂直的单位矢量．若 　=，试求tanA·tanB的值．

参考答案

一、1．B；

2．C；解：本题主要考查复数相等的充要条件及指数方程，对数方程的解法．

∵ ，∴，∴，

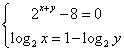解得或, ∴ z＝2＋i或z＝1＋2i．

诠释：本题应抓住复数相等的充要条件这一关键，正确、熟练地解方程（指数，对数方程）

3．B；

4．C；解析：∵ ∴ ，，∴ 集合中的元素为，选C．；

5．C；解：此题主要考查复数能比较大小的条件及方程组和不等式的解法．

∵ m²－(m²－3m)i＜(m²－4m＋3)i＋10, 且虚数不能比较大小，

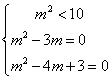∴，解得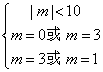，∴ m=3.

当m＝3时，原不等式成立．

诠释：本题应抓住复数能比较大小时必须都为实数这一条件．

6．D；7．A；8．C；

9．A；利用复数模的定义得<，选A；；

10．A；由复数模几何意义利用数形结合法求解，选A；

二、11．；12．x=, y=4；

13．i；解：此题主要考查iⁿ的周期性．

i＋i²＋i³+……+i²⁰⁰⁵=(i+i²+i³+i⁴)+……+(i²⁰⁰¹+i²⁰⁰²+ i²⁰⁰³＋i²⁰⁰⁴)＋i²⁰⁰⁵

=(i－1－i+1)+ (i－1－i+1)+……+(i－1－i+1)+i＝0＋0＋……＋0+i＝i.

或者可利用等比数列的求和公式来求解（略）

诠释：本题应抓住iⁿ的周期及合理分组．

14．xy=1；解：此题主要考查复数相等的充要条件，轨迹方程的求法．

∵ x＋yi=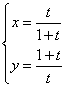，∴ ， ∴xy=1,

∴ 点(x，y)的轨迹方程为xy＝1，它是以x轴、y轴为对称轴，中心在(0，0)的等轴双曲线．

三、

15． 【分析】 利用复数模、四则运算的几何意义，将复数问题用几何图形帮助求解．

【解】 如图，设z＝、z＝后，则＝、＝如图所示．

y　　A 　　　　　 D 　　　O　 B 　　　 x 　　　　  　　　　　 C

由图可知，＝，∠AOD＝∠BOC，由余弦定理得：

cos∠AOD＝＝

∴ ＝(±ｉ)＝2±ｉ

y　　A 　　　　　 D 　　　O　 　　　　 x

【另解】设z＝、＝如图所示．则＝，且

cos∠AOD＝＝，sin∠AOD＝±，

所以＝(±ｉ)＝2±ｉ，即＝2±ｉ．

【注】本题运用“数形结合法”，把共轭复数的性质与复平面上的向量表示、代数运算的几何意义等都表达得淋漓尽致，体现了数形结合的生动活泼． 一般地，复数问题可以利用复数的几何意义而将问题变成几何问题，

16．解：此题主要考查复数的有关概念及方程（组）的解法．

（1）z为实数，则虚部m²+3m－10=0，即，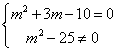

解得m=2，∴ m=2时，z为实数．

（2）z为虚数，则虚部m²+3m－10≠0，即，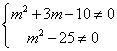

解得m≠2且m≠±5. 当m≠2且m≠±5时，z为虚数．，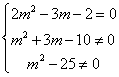

解得m=－, ∴当m=－时，z为纯虚数．

诠释：本题应抓住复数分别为实数、虚数、纯虚数时相应必须具备的条件，还应特别注意分母不为零这一要求．

17．分析与解答：

设z=a+bi (a,b∈R,且a²+b²≠0).

则

 

由(1)知是实数，且,

∴  即b=0或a²+b²=10.

又　 *

当b=0时，*化为无解．

当a²+b²=10时，*化为1<2a≤6, ∴.

由(2)知 a=1,2,3.

∴ 相应的b=±3, ±(舍)，±1，

因此，复数z为：1±3i或3±i.

此题不仅考查了复数的概念、运算等，同时也考查到了方程、不等式的解法．

18．分析与解答：设 z=a+bi, w=x+yi (a,b, x,y∈R).

由题z≠0, z≠2i 且z－i=1,

∴ a≠0, b≠0且a²+b²－2b=0.

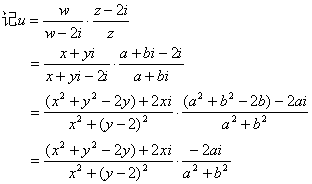
已知u为实数，

∴ ，

∵a≠0, ∴ x²+y²－2y=0 即 x²+(y－1)²=1.

∴w在复平面上所对应的点Z的集合是以(0, 1)为圆心，1为半径的圆．

又∵ w－2i≠0, ∴除去(0, 2)点．

此题中的量比较多，由于是求w对应点的集合，所以不妨设w为x+yi(x,y∈R), z=a+bi(a,b∈R).关于z和w还有一些限制条件，这些都对解题起着很重要的作用，千万不可大意．

19．分析与解答：

(1)∵z₁, z₂是一个实系数一元二次方程的两个虚根，因此必共轭，

可设z₁=a+bi(a,b∈R且b≠0),则z₂=a－bi,

由 得(a+bi)²=a－bi

即： a²－b²+2abi=a－bi

根据复数相等，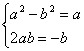

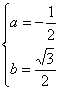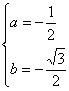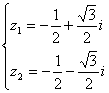∵b≠0 解得： 　或　 ，

∴  或 　．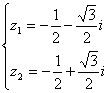

(2)由于 ，z₁=1+mi, w=z₂+3,　

∴w=(1+mi)²+3=4－m²+2mi.

∴ ,

由于且m≠0, 可解得0<m²≤1,

令m²=u, ,

在u∈(0,1)上，(u－2)²+12是减函数，∴.

复数这一章中去掉了三角形式,降低了难度，但在复数的基本概念、运算、复数与方程、复数与几何这些部分仍然有许多可考查的内容，并且还可以与其它的数学知识相结合．

20．讲解：从化简变形 入手．

²=()²=()²

=

= ，

=，

cos(A－B)=cos(A+B)．

4 cosA·cosB+4sinA·sinB=5cosA·cosB–5sinA·sinB，　

9sinA·sinB= cosA·cosB．

又A、B是ABC的内角，

 cosA·cosB，　  tanA·tanB=．

说明：本题将复数、三角、向量溶为一体，综合性较强．