高二上期末考试模拟试题十一
数 学
（测试时间：120分钟 满分150分）
第 I 卷
一. 选择题 (本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)
1．直线x+y-1=0的倾斜角为（ ）
A、
B、- C、
D、-
2．若a、b、c∈R，则下列命题正确的是（ ）
A、a＞b,c＞d＞
ac＞bd
B、
＞
a＞b
C、a3＞b3且ab＞0
＜
D、a2＞b2且ab＞0＜
3.抛物线y=x2的焦点坐标为（ ）
A、（0，
） B、（0，
） C、（，0） D、（，0）
4．圆x2 + y2－2 x = 0和 x2 + y2 ＋4y = 0的位置关系是（ ）
A. 相离 B. 外切
C. 内切 D. 相交
5.下列不等式中与x＜3同解的不等式是（ ）
A、x+
＜3+ B、x+
＜3+
C、x(x+4)2＜3（x+4）2 D、x(x-4)2＜3（x-4）2
6．a=2是直线x+ay-a=0与直线ax-(2a-3)y-1=0互相垂直的（ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、非充分也非必要条件
7、下列函数中，最小值是2的是（ ）
A、y=x+
B、y=tanθ+cotθ, θ∈(0,
)
C、y=sinθ+cscθ, θ∈(0, )
D、y=
+
8、若直线ρ1、ρ2的斜率是方程x2-4x+1=0的两根，则ρ1、ρ2的夹角为（ ）
A、
B、
C、 D、
9、若
，
，
，
，则（ ）
（A）
（B）
（C）
（D）
10．已知椭圆的焦点是F1、F2，P是椭圆上的一个动点，如果延长F1P到Q，使得 PQ =
PF2 ，那么动点Q的轨迹是（ ）
A. 圆 B. 椭圆
C. 双曲线的一支 D. 抛物线
11、已知曲线bx2+ay2=ab与直线ax+by+1=0(a,b为非零实数)，在同一坐标系中，它们的图形可能是（ ）
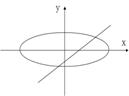
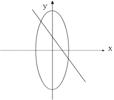
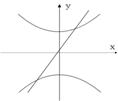
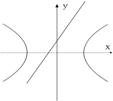
A B C D
12.若对于任意的实数，不等式｜x＋1｜≥kx恒成立，则实数k的取值范围是 （ ）
A．(－∞，0) B．[－1，1] C．[0，1] D．[1，＋∞]
二. 填空题 (本大题共4小题，每小题4分，共16分. 把答案填在题中横线上.)
13.不等式
的解集为________________________
14. 已知圆 x2 + y2－6x－7 = 0与抛物线y2 = 2px ( p> 0 ) 的准线
相切，则 p = .
15. 不等式组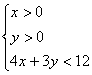
表示的平面区域内的整点（横坐标和纵坐标都是整数的点）
共有 个.
16. 对于椭圆
和双曲线
有下列命题：
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
二. 填空题 (本大题共4小题，每小题4分，共16分. 把答案填在题中横线上.)
13. ________________________ 14. p = .
15. 共有 个. 16. 其中正确命题的序号是 .
三. 解答题 (本大题共5小题，共56分. 解答应写出文字说明，证明过程或演算步骤.)
17. （本小题满分10分）解关于x的不等式
＞1（a∈R）
18. （本小题满分10分）椭圆焦点F1（-2，0），F2（2，0），椭圆经过点A（
，
）
⑴.求椭圆方程。
⑵.若椭圆上一点P到左焦点F1的距离为3，求该点到右准线的距离。
19．（本小题满分10分）
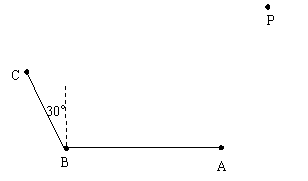
有三个信号监测中心A、B、C，A位于B的正东方向, 相距6千米, C在B的北偏西
，相距4千米. 在A测得一信号，4秒后, B、C才同时测得同一信号，试建立适当的坐标系，确定信号源P的位置. (即求出P的坐标. 设该信号的传播速度为1千米/秒)
20．（本小题满分12分）已知a,b>0,a+b＝1.求证：(1+)(1+)≥9.
21.（本小题满分14分）
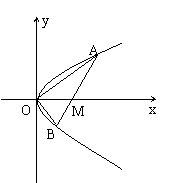如图，已知直线l与抛物线y2 = x相交于A（x1，y1），B（x2，y2）两点，与x轴相交于点M，若y1y2
= －1，
（1）求证：M点的坐标为（1，0）；
（2）求证：OA⊥OB；
（3）求△AOB的面积的最小值.
参 考 答 案
一. 选择题 （将正确答案的代号填入下表内）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | B | D | D | A | B | B | B | A | D | C |
第 II 卷
二. 填空题 (本大题共4小题，每小题4分，共16分. 把答案填在题中横线上.)
13. ____(1,3)∪(3,5)_______ 14. p = 2
15. 共有 3 个. 16. 其中正确命题的序号是 (1) (2) .
三. 解答题 (本大题共5小题，共56分. 解答应写出文字说明，证明过程或演算步骤.)
17. （本小题满分10分）
解：原不等式可化为
＞0
（1）当a＞0时，解集为{x│x＜-
或x＞a}
（2）当a＜0时，解集为{x│x＜a或x＞-}
（3）当a≠0时，解为{x│x∈R且x≠0}
18. （本小题满分10分）
解:(1)
, (2)
19．（本小题满分10分）
解：取A、B所在直线为x轴，线段AB的中点O为原点，建立直角坐标系. 则A、B、C的坐标为A ( 3, 0 )、B (－3, 0 )、C (－5, 2
), (长度单位为千米).
由已知 PB － PA = 4, 所以点P在以A、B为焦点，实轴长为4的双曲线的右支上，
其方程为
（x≥2）
①
又B、C同时测得同一信号，即有 PB = PC
∴ 点P又在线段BC的中垂线上，
其方程为
即 
②
由①、② 可得点P的坐标为 ( 8, 5).
20．（本小题满分12分）
证：∵a,b>0,a+b＝1.
∴(1+)(1+)= (1+
) (1+
)= (2+
) (2+
)= 4+2 (+)+1
= 5+2 (+) ≥ 5+2×2 (
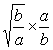) = 9
21.（本小题满分14分）
解:1 ) 设M点的坐标为（x0, 0）, 直线l方程为 x = my + x0 , 代入y2 = x得
y2－my－x0 = 0 ① y1、y2是此方程的两根,
∴ x0 ＝－y1y2 ＝1，即M点的坐标为（1, 0）.
(2 ) ∵ y1y2 ＝－1
∴ x1x2 + y1y2 = y12y22 +y1y2 ＝y1y2 (y1y2 +1) = 0
∴ OA⊥OB.
（3）由方程①，y1＋y2 = m , y1y2 ＝－1 , 且 OM = x0 =1,
于是S△AOB =
OM y1－y2 =
=
≥1，
∴ 当m = 0时，△AOB的面积取最小值1.