高二上期末考试模拟试题十二
数 学
(测试时间:120分钟 满分150分)
第 I 卷
一.选择题 1.已知F是抛物线![]()
![]() 的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.若双曲线的两条渐近线方程是![]() x,焦点 F
x,焦点 F![]() (
(![]() ),
), ![]() (
(![]() ) ,那么它的两条准线间的距离是( )
) ,那么它的两条准线间的距离是( )
(A). ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
3.点P(-3,1)在椭圆![]()
![]()
![]() 的左准线上,过点P且方向为
的左准线上,过点P且方向为![]() 的光线,经直线y=-2 反射后通过椭圆的左焦点,则这个椭圆的离心率是( )
的光线,经直线y=-2 反射后通过椭圆的左焦点,则这个椭圆的离心率是( )
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)![]()
4.当曲线![]() 与直线y=k(x-2)+4有两个相异交点时, 实数k的取值范围( )
与直线y=k(x-2)+4有两个相异交点时, 实数k的取值范围( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
5.已知A,B是平面上的两个定点,M是以A为圆心定长L为半径的圆上的 一个动点,线段MB的中垂线交直线MA于点P,则点P的集合构成的图形是( )
(A)椭圆 (B) 双曲线的一支 (C) 抛物线 (D)不能确定
6.已知k是常数,若双曲线![]() 的焦距与k的取值无关,则k的取值范是
的焦距与k的取值无关,则k的取值范是
(A)-2<k![]() (B)k>5 (C)
(B)k>5 (C) ![]() (D)
(D)![]()
7.若直线y=kx+2与双曲线![]() 的右支有两个不同的交点,则k的取值范围是( )
的右支有两个不同的交点,则k的取值范围是( )
(A) 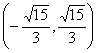 (B)
(B) 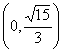 (C)
(C) 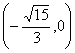 (D)
(D) 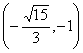
8.已知直线L交椭圆 ![]() 于M,N两点,椭圆于y轴的正半轴交于点B,若
于M,N两点,椭圆于y轴的正半轴交于点B,若![]() 的重心恰好落在椭圆的右焦点上,则直线L的方程是( )
的重心恰好落在椭圆的右焦点上,则直线L的方程是( )
(A)5x+6y-28=0 (B) 5x-6y-28=0 (C) 6x+5y-28=0 (D) 6x-5y-28=0
9.已知点A(5,2),F是双曲线 ![]() 的右焦点,M是双曲线右支上的一点,则
的右焦点,M是双曲线右支上的一点,则![]() 的最小值是( ) (A)9 (B)12 (C)16 (D)20
的最小值是( ) (A)9 (B)12 (C)16 (D)20
10.一抛物线型拱桥,当水面离桥顶
(A)![]() 米 (B)
米 (B)![]() 米 (C)
米 (C)
11.一个酒杯的截面是抛物线的一部分,它的方程是![]() ,在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为( )
,在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
12.已知x,y满足: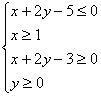
![]() ,则
,则![]() 的最值是( )
的最值是( )
(A)最大值为2,最小值为0 (B)最大值为2,无最小值
(C)无最大值,最小值为0 (D)无最值
二.填空题(每题4分,共16分)
13.已知圆上点A(1,0)关于直线x+2y-3=0的对称点仍然在这个圆上,且直线x+2y-3=0被圆截得的弦长为4,则这个圆的方程是
14.以定点A(2,8)和动点B为焦点的椭圆经过点P(-4,0),Q(2,0),则动点B的轨迹方程是
15.某宇宙飞船的运行轨道是以地球的中心F为左焦点的椭圆,测得近地点A距离地面m km,远地点B距离地面n km,地球的半径为R km,关于椭圆有以下四种说法:
(1)焦距长为n-m (2)短轴长为![]() (3)
离心率
(3)
离心率![]()
(4)以AB方向为x轴的正方向,F为坐标原点,则左准线方程为![]() ,
,
以上说法正确的是
16.若x,y为整数,则称坐标平面上的点(x,y)为格点,直线![]() 与格点的距离的最小值是
与格点的距离的最小值是
三.解答题:
17.已知双曲线的中心在原点,焦点![]() 在坐标轴上,离心率为
在坐标轴上,离心率为![]() ,且过点
,且过点![]() ,
,
(1)求双曲线方程。
(2)若点M(3,m)在双曲线上,求证:![]() 。
。
(3)求:![]() 的面积。
的面积。
18.已知中心在原点的椭圆C的两个焦点和椭圆![]() :
:![]() 的两个焦点是一个正方形的四个顶点,且椭圆C过点A(2,-3),
的两个焦点是一个正方形的四个顶点,且椭圆C过点A(2,-3),
(1)求椭圆C的方程
(2)若PQ是椭圆C的弦,O是坐标原点,![]() ,且点P的坐标为
,且点P的坐标为![]() ,求点Q的坐标。
,求点Q的坐标。
19.已知圆![]()
(1)求证:不论m为何值,圆心在同一直线L上。
(2)与L平行的直线中,哪些与圆相交,相切,相离;
(3)求证:任何一条平行于L且与圆相交的直线被圆截得的弦长![]() 相等。
相等。
20.设A![]() ,B(
,B(![]() )两点在抛物线
)两点在抛物线![]() 上,L是AB得垂直平分线,
上,L是AB得垂直平分线,
(1)当且仅当![]() 取何值时,直线L经过抛物线得焦点F?证明你的结论;(2)当
取何值时,直线L经过抛物线得焦点F?证明你的结论;(2)当![]() 时,求直线L得方程。
时,求直线L得方程。
21.如图所示,线段AB=4,动圆![]() 与线段AB切于点C,且
与线段AB切于点C,且![]() =
=![]() ,过点A,B分别作圆
,过点A,B分别作圆![]() 的切线,两切线相交于P,且P
的切线,两切线相交于P,且P![]() 均在AB的同侧,
均在AB的同侧,
(1)建立适当的坐标系,当![]() 位置变化时,求动点P的轨迹E的方程;
位置变化时,求动点P的轨迹E的方程;
(2)过点B作直线L交曲线E于点M,N,求![]() 面积的最小值。
面积的最小值。
 | |||
 | |||
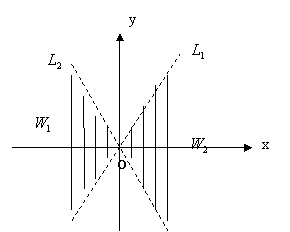
22如图,直线![]() :y=kx(k>0)与直线
:y=kx(k>0)与直线![]() :y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为
:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为![]() ,右半部分记为
,右半部分记为![]() ,
,
(1) 分别用不等式组表示![]() 和
和![]() ;
;
(2) 若区域W中的动点P(x,y)到![]() ,
,![]() 的距离之积等于
的距离之积等于![]() ,求点P的轨迹C的方程;
,求点P的轨迹C的方程;
(3) 设不过原点O的直线L与(2)中的曲线C相交与![]() ,且与
,且与![]() ,
,![]() 分别交于
分别交于![]() 两点,求证:
两点,求证:![]() 的重心与
的重心与![]() 的重心重合。
的重心重合。
答案
一.选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | A | B | C | D | C | D | D | A | B | A | A |
二,填空题
13. ![]() 或
或![]() 14. 双曲线
14. 双曲线![]() 的右支
的右支
15.(1)(3)(4)
16. ![]()
三.解答题
17.(1)因为 e=![]() 所以设双曲线方程为
所以设双曲线方程为![]() ……………………
……………………
因为过(4,![]() )点,所以16-10=
)点,所以16-10=![]() ,即
,即![]() =6,
=6,
所以双曲线方程为![]()
(2)易知![]() ,
,![]() ,所以
,所以![]() ,
,![]()
所以![]() 。
。![]() =
=![]() ………………………………………………6
………………………………………………6
因为点(3,m)在双曲线上,所以9-![]() =6,
=6,![]() =3
=3
故![]() 。
。![]() =-1,
=-1,![]()
![]()
![]() ………………………………………………8
………………………………………………8
(3)![]() 的底
的底![]() =4
=4![]() ,其高为h=
,其高为h=![]() =
=![]()
所以![]() =6………………………………………………………………………12
=6………………………………………………………………………12
18.椭圆![]() :
:![]() 的两个焦点
的两个焦点![]() (
(![]() ),
),![]() (
(![]() ),
),
又椭圆C与椭圆![]() 的焦点
的焦点![]() ,
,![]() ,
,![]() ,
,![]() 是一个正方形的四个顶点,椭圆C的中心在原点,
是一个正方形的四个顶点,椭圆C的中心在原点,
所以![]() ,
,![]() 关于原点对称,所以
关于原点对称,所以![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() )
)
故椭圆方程C可以设为:![]()
![]() ………………………………3
………………………………3
因为椭圆C过点A(2,-3),所以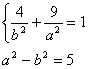
![]() ,解得,
,解得,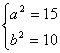 或
或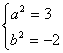 (舍)
(舍)
所以椭圆C的方程是![]() …………………
…………………![]() …………………………………6
…………………………………6
(2)设Q(![]() ,
,![]() ),因为OP
),因为OP![]() OQ,所以
OQ,所以![]() 。
。![]() =
=![]() 。
。![]() =-1
=-1
所以![]() =-
=-![]()
![]() 又因为
又因为![]() ,所以
,所以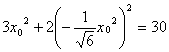 ,
,
即![]()
![]() ,则
,则![]() 或
或![]()
故点Q为![]() 或
或![]() ………………………………………………………………12
………………………………………………………………12
19.解 (1)配方得![]() ,设圆心为(x,y)
,设圆心为(x,y)
则![]() 消去m得L :x-3y-3=0…………………………………………………………2
消去m得L :x-3y-3=0…………………………………………………………2
则圆心恒在直线L::x-3y-3=0上………………………………………………………………4
(2)设与L平行的直线是![]() :x-3y+b=0,则圆心到直线
:x-3y+b=0,则圆心到直线![]() 的距离为
的距离为![]() ………………………………………………………………6
………………………………………………………………6
因为圆的半径为r=5,所以
当d<r时即![]() <b<
<b<![]() 时,直线与圆相交,
时,直线与圆相交,
当d=r时,即b=![]() 时,直线与圆相切,
时,直线与圆相切,
当d>r时,即b<![]() 或b>
或b>![]() 时,直线与圆相离,…………………………8
时,直线与圆相离,…………………………8
(3)对于任一平行L且与圆相交的直线![]() :x-3y+b=0,由于圆心到直线
:x-3y+b=0,由于圆心到直线![]() 的距离
的距离![]() ,从而弦长=
,从而弦长=![]() 与m无关,
与m无关,
所以任何一条平行于L且与圆相交的直线被圆截得的弦长都相等,………………12
20.解 (1)因为F∈L,∴∣FA∣=∣FB∣∴A,B两点到抛物线的准线的距离相等----2分
∵抛物线的准线是X轴的平行线,y1≥0,y2≥0,依题意y1,y2不同时为0,所以上述条件等价于y1=y2![]() x
x![]() =x
=x![]()
![]() (x1+x2)(x1-x2)=0 ----------4分
(x1+x2)(x1-x2)=0 ----------4分
∵x1![]() x2,上述条件等价于x1+x2=0,既当且仅当x1+x2=0时,L经过抛物线的焦点F
x2,上述条件等价于x1+x2=0,既当且仅当x1+x2=0时,L经过抛物线的焦点F
-------6分
(2)![]() =
=![]() =2,
=2,![]() =18
=18
∴过点AB的直线的斜率为![]()
![]()
![]() ---8分
---8分
∵L与AB垂直∴L的斜率为![]() ------------------------10分
------------------------10分
又线段AB的中点坐标为(![]() 即(-1,10)
即(-1,10)
∴L的直线方程为y-10=![]() (x+1)
(x+1)
即所求的方程为x-4y+41=0--------------------------12分
21.解 (1)以线段AB所在直线为x轴,线段AB的中垂线为y轴,建立直角坐标系,…1
如图,设P(x,y),因为![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ………………………………2
………………………………2
所以![]() -
-![]() =
=![]() -
-![]() =
=![]() <4,所以点P的轨迹是以A,B为焦点,
<4,所以点P的轨迹是以A,B为焦点,![]() 为实轴长的双曲线的右支(除去与x轴的交点),a=
为实轴长的双曲线的右支(除去与x轴的交点),a=![]() ,c=2,所以
,c=2,所以![]() =2,所以点P的轨迹E的方程是
=2,所以点P的轨迹E的方程是![]() (
(![]() )………………………………………………………………6
)………………………………………………………………6
| |||
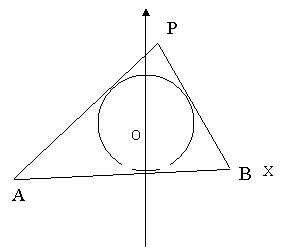 | |||
|
令![]() =
=![]() (-1<
(-1<![]() <1),
<1),
则MN:x=![]() y+2,…………………………………………………………………………8
y+2,…………………………………………………………………………8
由x=![]() y+2,
y+2,![]() (
(![]() )消去x得
)消去x得
(![]() -1)
-1)![]() +4
+4![]() y+2=0,设M(
y+2=0,设M(![]() ),N(
),N(![]() ),则
),则![]() =
=![]() ,
,
![]() =
=![]()
![]() .
.![]() =
=![]()
![]() 4
4![]()
![]() =
=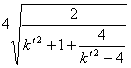 …………10
…………10
因为1![]()
![]() <2,所以4<
<2,所以4<![]() +1+
+1+![]()
![]() 1+4=5
1+4=5
所以0<![]() +1+
+1+![]() -4
-4![]() 1,所以
1,所以![]()
![]()
![]()
当![]() =0,即MN
=0,即MN![]() x轴时,
x轴时,![]() 有最小值
有最小值![]() 。…………………………………12…
。…………………………………12…
