高二上期末考试模拟试题十四
数 学
(测试时间:120分钟 满分150分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.不等式x.(x-2)≥0的解集是( )
A.{xx≥2} B.{xx≥2或x=0} C.{xx>2} D.{xx>2或x=0}
2.抛物线y=-2x2的焦点坐标是( )
A.(0,-![]() ) B.(0,-
) B.(0,-![]() ) C.(-
) C.(-![]() ,0) D.(-
,0) D.(-![]() ,0)
,0)
3.若双曲线![]() -
-![]() =l上一点P到它的右焦点的距离为4,则点P到它的左准线的距离为( )
=l上一点P到它的右焦点的距离为4,则点P到它的左准线的距离为( )
A.![]() B.4 C.
B.4 C.![]() D.8或
D.8或![]()
4.过点P(-2,1)的直线l到A(-4,1),B(0,3)的距离相等,则直线l的方程为( )
A.x-2y+4=O B.x=-2 C.x-2y+4=O或x=-2 D.x-2y+4=O或y=-2
5.满足约束条件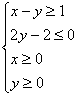 的目标函数z=2x+2y的最小值是( )
的目标函数z=2x+2y的最小值是( )
A.-2 B.-l C.1 D.2
6.若x-a<q,y-a<q,(q>O),则下列不等式一定成立的是( )
A.x-y<q B.x-y>q C.x-y<2q D.x-y>2q
7.若(x-2)2+y2=l,则x+y的最小值为( )
A.-![]() B.1 C.2+
B.1 C.2+![]() D.2-
D.2-![]()
8.抛物线的顶点为原点,焦点在y轴上,抛物线上点M(m,-2)到焦点的距离为4,则m的值为( )
A.4 B.-2 C.4或-4 D.2或-2
9.直线l1过点P(1,2),且斜率为3,直线l1与l2关于y轴对称,则l2的方程是( )
A.3x+y-l=0 B.x+3y-l=0 C.3x+y+1=0 D.x+3y+1=0
10.若圆x2+y2=r2(r>0)上恰有相异两点到直线 4x-3y+25=O的距离等于1,则r的取值范围是 ( )
A.[4,6] B.(4,6) C.(4,6) D.[4,6]
11.给定四条曲线
①x2+y2=![]() ,②
,②![]() +
+![]() =1,③x2+
=1,③x2+![]() =1, ④
=1, ④![]() +y2=1,其中与直线x+y-
+y2=1,其中与直线x+y-![]() =0仅有一个公共点的曲线是( )
=0仅有一个公共点的曲线是( )
A.①②③ B.②③④ C.①②④ D.①③④
12.某厂的某种产品的产量第二年增长率为pl,第三年增长率为p2,且p1>0,p2>0,pl+p2=p,p为常数,如果这两年的平均增长率为x,则有( )
A.x≤![]() B.x =
B.x = ![]() C. x<
C. x<![]() D.x≥
D.x≥![]()
二、填空题(本大题共4小题,每小题4分,共16分,把正确答案填在题中横线上)
13.直线x+my-3=0与直线2mx-(m-1))y+5=O互相垂直,则m的值为________.
14.已知双曲线的渐近线方程是y=±![]() x,则此双曲线的离心率是_______.
x,则此双曲线的离心率是_______.
15.不等式![]() <1的解集是{x x<1或x>2},则a=______________.
<1的解集是{x x<1或x>2},则a=______________.
16.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则P的值为____.
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或推演步骤)
17.(12分)已知双曲线与椭圆![]() +
+![]() =1共焦点,它们的离心率之和为
=1共焦点,它们的离心率之和为![]() ,求双曲线方程.
,求双曲线方程.
18.(12分)不等式![]() <0对一切实数x恒成立,求实数m的取值范围.
<0对一切实数x恒成立,求实数m的取值范围.
19.(12分)已知圆上点A(2,3)关于直线x+2y=0的对称点仍在圆上,且该圆截直线x-y+1=0所得的弦长为2![]() ,求此圆的方程.
,求此圆的方程.
20.(12分)有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:每单位距离A地的运费是B地运费的3倍,已知A、B两地相距10千米,顾客选择A或B地购买这件商品的标准是:包括运费和价格的总费用较低,求A、B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民如何选择购货地点.
21.(12分)已知椭圆的中心为原点,焦点在x轴上,过它的右焦点引倾斜角为![]() 的直线l交椭圆于P、Q两点,P、Q到椭圆的右准线的距离之和为
的直线l交椭圆于P、Q两点,P、Q到椭圆的右准线的距离之和为![]() ,它的左焦点到l的距离为
,它的左焦点到l的距离为![]() ,求椭圆的方程.
,求椭圆的方程.
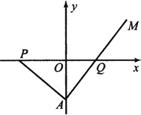 22.(14分)如图,已知直角ΔPAQ的顶点P(-4,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=900,在AQ的延长线上取一点M,使QM-AQ.
22.(14分)如图,已知直角ΔPAQ的顶点P(-4,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=900,在AQ的延长线上取一点M,使QM-AQ.
(1)当A点在y轴上移动时,求动点M的轨迹E;
(2)已知D(1,0),是否存在过点F(-1,0)的直线l交轨迹E于两点B、C,满足∠BDC=900,若存在,求出直线l的方程;若不存在,说明理由.
参考答案
1.B 2.A 3.C 4.C 5.D 6.C 7.D 8.C 9.C 10.B 11.D 12.A
一、解析
1. ∵x≥0恒成立,∴原不等式等价于x=0或x-2≥0,故 x=0或x≥2.
2. 将抛物线方程化为标准形式x2=-![]() y,开口向下,2p=
y,开口向下,2p=![]() ,∴焦点(0,-
,∴焦点(0,-![]() ).
).
3. ∵a=2,b=![]() ,∴c=3,a+c=5. ∴双曲线左支上的点到右焦点的距离d≥5,因此点P应在双曲线右支上.∴PF1-4=2a=4,PF1=8,又
,∴c=3,a+c=5. ∴双曲线左支上的点到右焦点的距离d≥5,因此点P应在双曲线右支上.∴PF1-4=2a=4,PF1=8,又![]() =
=![]() =
=![]() , ∴d=
, ∴d=![]() .
.
4. ∵直线l到A、B两点距离相等, ∴Z应过AB的中点或与AB平行,易求得答案C.
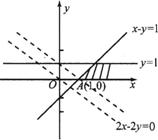 5.画出可行域如图,平移直线2x+2y=O,当它经过点A(1,O)时,对应的目标函数z取得最小值, Zmin=2×l+2×0=2
5.画出可行域如图,平移直线2x+2y=O,当它经过点A(1,O)时,对应的目标函数z取得最小值, Zmin=2×l+2×0=2
6. x-y=(x-a)-(y-a)≤x-a+y-a<q+q=2q.
7.可设![]() ∴x+y=sin
∴x+y=sin![]() +cos
+cos![]() +2 =
+2 =![]() sin(
sin(![]() )+2
)+2
∴x+y的最小值为2-![]() .
.
8.根据题意可设抛物线方程为x2=-2py,由抛物线的定义知,点M到准线的距离等于到焦点的距离,即![]() +2=4, ∴p=4. ∴抛物线方程为x2=-8y,把(m,-2)代入得m=±4.
+2=4, ∴p=4. ∴抛物线方程为x2=-8y,把(m,-2)代入得m=±4.
9.l1的方程为y-2=3(x-1),即3x-y-l=0, 设P(x,y)是l2上任一点,∵l1与l2关于y轴对称, ∴p/(-x,y)一定在l1上,代入l1的方程得-3x-y-1=0 即3x+y+l=0,这就是l2的方程.
10. ∵圆心(0,0)到直线4x-3y+25=0的距离d=![]() =5. 结合图形易知4<r<6.
=5. 结合图形易知4<r<6.
11.①圆心(0,0)到直线x+y-![]() =0的距离d=
=0的距离d=![]() =
=![]() = r, ∴圆与直线相切,故①符合,排除(B). 由
= r, ∴圆与直线相切,故①符合,排除(B). 由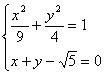 得13x2-18
得13x2-18![]() x+9=0,△>0,∴直线与椭圆相交,故②不符合,应排除(A)、(C)、故选(D).
x+9=0,△>0,∴直线与椭圆相交,故②不符合,应排除(A)、(C)、故选(D).
12.设第一年的产量为1,则第二年的产量为l+p1,第三年的 产量为(1+p1)(1+p2)又两年的平均增长率为x,则第二年 的产量为1+x,第三年的产量为(1+x)2
∴(1+x)2=(1+p1)(1+p2)≤(![]() )2=(1+
)2=(1+![]() )2
∴1+x≤1+
)2
∴1+x≤1+![]() ,x≤
,x≤![]() .
.
13.0或3 14.![]() 或
或![]() 15.
15.![]() 16.2,
16.2,
二、解析:
13.两直线垂直的充要条件是A1A2+BlB2=0,∴2m-m(m-1)=0,∴m=O或3
14.若焦点在x轴上,则![]() =
=![]() ,
,![]() =
=![]() =
=![]() =
=![]() =
=![]() .若焦点在y轴上,则
.若焦点在y轴上,则![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() =
=![]() .
.
15.原不等式可化为![]() <0, 分子,分母的根分别为
<0, 分子,分母的根分别为![]() ,1, ∵不等式的解集为{xx<1或x>2}, ∴
,1, ∵不等式的解集为{xx<1或x>2}, ∴![]() =2,a=
=2,a=![]() .
.
16.圆x2+y2-6x-7=O的标准方程为(x-3)2+y2=16, ∴圆心为(3,0),半径为4, 根据题意3+![]() =4,p=2.
=4,p=2.
17.解:椭圆![]() +
+![]() =1的焦点为(0,4),(0,-4),
由题意设双曲线方程为
=1的焦点为(0,4),(0,-4),
由题意设双曲线方程为![]() -
-![]() =l(a>0,b>0),则
=l(a>0,b>0),则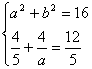 ∴a=2,b2=12, ∴所求的双曲线的方程为
∴a=2,b2=12, ∴所求的双曲线的方程为![]() -
-![]() =1.
=1.
18.解:∵x2-8x+20=(x-4)2+4>0, ∴原不等式等价于:mx2-x-l<0对x∈R恒成立.当m=0时,-1<0恒成立,符合题意. m≠0时,则![]() 即
即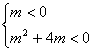 解得:-4<m<O, 综上,得 -4<m≤O
解得:-4<m<O, 综上,得 -4<m≤O
19.解:由题意知:圆心在直线x+2y=0上. 设圆的圆心为(a,b),半径为r,是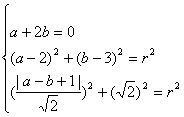 解得
解得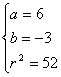 或
或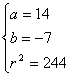 ∴所求圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244
∴所求圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244
20.解:以AB所确定的直线为x轴,线段AB的中点为坐标原点,建立直角坐标系. ∵AB=10,设A(-5,O)、B(5,0), 设某地P处居民选择A地购物便宜,并设A地的运费为3a元/千米,B地的运费为a元/千米. ∵P(x,y)地的居民购物总费用满足条件:价格+A地运费≤价格+B地运费, 即3a![]() ≤a
≤a![]() , ∵a>0, ∴8x2+8y2+lOOx+200≤0 得(x+
, ∵a>0, ∴8x2+8y2+lOOx+200≤0 得(x+![]() )2+y2≤(
)2+y2≤(![]() )2 , ∴以点C(-
)2 , ∴以点C(-![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆,是这两地购物区域的分界线. 圆C内的居民从A地购物便宜,圆C外的居民从B地购物便宜.圆C上的居民从A、B两地购物的总费用相等,可随意选择一地购物.
为半径的圆,是这两地购物区域的分界线. 圆C内的居民从A地购物便宜,圆C外的居民从B地购物便宜.圆C上的居民从A、B两地购物的总费用相等,可随意选择一地购物.
2l.解:设椭圆方程为![]() +
+![]() =1(a>b>0),P(x1,y1),Q(x2,y2)左焦点F1(-c,0),右焦点F2(c,0),(c>0). 直线l的方程:y=(x-c)tan
=1(a>b>0),P(x1,y1),Q(x2,y2)左焦点F1(-c,0),右焦点F2(c,0),(c>0). 直线l的方程:y=(x-c)tan![]() 即y=x-c, 由(-c,0)到l的距离为
即y=x-c, 由(-c,0)到l的距离为![]() ,得
,得![]() =
=![]() ∴c=1, 则a2-b2=1, ∴椭圆方程为
∴c=1, 则a2-b2=1, ∴椭圆方程为![]() +
+![]() =1,
=1, 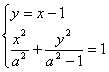 消去y整理得
(2a2-1)x2-2a2x+2a2-a4=O ∴x1+x2=
消去y整理得
(2a2-1)x2-2a2x+2a2-a4=O ∴x1+x2=![]() ………………………… ①
………………………… ①
P、Q到右准线距离之和为:![]() -x1+
-x1+![]() -x2=
-x2=![]() , 即x1+x2=2a2-
, 即x1+x2=2a2-![]() ………………………②
………………………②
由①②得a2=2,
∴b2=1, ∴椭圆方程为![]() +y2=1
+y2=1
22. 解:(1)设M(x,y),A(0,b),Q(a,0)(a>0),由QM=AQ知Q是AM的中点,则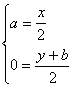
∴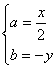 ……………………………………………①
……………………………………………①
由∠PAQ=900 知![]() =-1………………②
=-1………………②
①代入②并化简得y2=2x ∴动点M的轨迹方程y2=2x (x≠0), 轨迹是:顶点为原点,焦点为(![]() ,0)的抛物线(顶点除外)
,0)的抛物线(顶点除外)
(2)假设存在,设直线l的方程为:y=k(x+1),B(x1,y1),C(x2,y2), 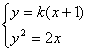 消去y并整理得:k2x2+(2k2-2)x+k2=0,
则
消去y并整理得:k2x2+(2k2-2)x+k2=0,
则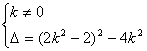 ∴-
∴-![]() <k<
<k<![]() 且k≠0 …………(*)
且k≠0 …………(*)
x1+x2=![]() ,x1x2=1,∴y1y2=k(x1+1)·k(x2+1)=k2(x1x2+x1+x2+1)=2
,x1x2=1,∴y1y2=k(x1+1)·k(x2+1)=k2(x1x2+x1+x2+1)=2
∵∠BDC=900 ∴![]() ·
·![]() =-1, 即y1y2+x1x2-(x1+x2)+l=0
=-1, 即y1y2+x1x2-(x1+x2)+l=0
∴2+-![]() =0, ∴k=±
=0, ∴k=±![]() 满足(*)
满足(*)
故直线l存在,直线l的方程为y=±![]() (x+1)
(x+1)
即x-![]() y+1=0或x+
y+1=0或x+![]() y+1=0
y+1=0
|