高二数学上期末考试模拟试题十五
数 学
（测试时间：120分钟 满分150分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知
，则
是a 2 > b
2 的（ ）
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2. 下列不等式中，对任意
恒成立的是（ ）
A.
B.
C.
D.
3. 设
，则下列不等式中不成立的是（ ）
A.
B.
C.
D.
4. 设
，
，则（ ）
A.
B.
C.
D.不能确定
5. 函数
的最大值是（ ）
A.
B.
C.
D.
6. 设
，则
（ ）
A.有最小值
B.有最小值
C.有最大值 D.有最大值
7. 设，下列结论不正确的是（ ）
A.
B.
C.
D.
8. 设
，则
中最大的一个是( )
A.
B.
C.
D.不能确定
9. 若
，则下列结论不正确的是（ ）
A.
B.
C.
D.
10. 已知实数、满足
，则（ ）
A.
B.
C.
D.
11. 如果，则下列不等式：
①
； ②
； ③
；
④
中成立的是( )
A.①②③④ B.①②③ C.①② D.③④
12. 若
都是正数，且
，则
的最小值为（ ）A.
B.
C.
D.
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.
13. 设
，则
的取值范围是_______________；
14. 已知
，且
，则4＋
的最小值是_______________；
15. 若
，
，
，则
与
的大小关系是______________；
16. 对实数与
而言，
成立的充要条件是_____________；
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.
17. （本小题满分12分）
已知
，
，
，比较
与
的大小；
18.
（本小题满分12分）
若，
，求证：
；
19.
（本小题满分12分）
设
，用分析法证明：
；
20.
（本小题满分12分）
已知
为正数，
（1）求证：
（2）求证：
；
21.
（本小题满分12分）
已知，求证：
22.
（本小题满分14分）
是否存在常数
，使得不等式
对任意正数、
恒成立？证明你的结论。
参考答案
1. B
2. C
3. D
4. A
5. A
6. D
7. A
8. C
9. D
10. B
11. A
12. B
13. 
14. 2
15. 
16. 
17. 解：
，,
,
,
,即
18. 证明：
（1）当时，
，
（2）当
时，
（3）当
时，
，
综上，
，当且仅当
时取等号。
19.
证明：
，
要证，只要证
，
即证
，
，
，即
所以；
20.
证明
（1）由为正数，
，得；
（2）由（1），同理
，
三式相加即得；
21.
证法一：
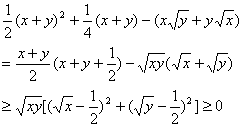
证法二：
22. 解：令
，得
，
先证
，要证，
只要证
即证
，这显然成立，
再证
只要证
即证
，这显然成立，
综上所述，存在常数，使得不等式对任意正数、恒成立。
|