高二上期末考试模拟试题九
数 学
（测试时间：120分钟 满分150分）
一、选择题（本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中， 只有一项是最符合题目要求的）
1、直线
和直线
的位置关系是
（ ）
A、垂直 B、平行 C、关于x 轴对称 D、关于y轴对称
2、下列命题中,真命题是 （ ）
A、空间三点确定一个平面 B、有三个公共点的两平面必重合
C、不共面的四点中，任何三点不共线 D、两条垂直直线确定一个平面
3、直线
被曲线
（
为参数）所截线段的长度是
（ ）
A、
B、1
C、
D、2
4、边长为2的正三角形的斜二测画法的直观图的面积为 （ ）
A、
B、
C、
D、
5、用一个平面去截一个正方体得到的多边形，其中边数最多的是 （ ）
A、四边形 B、五边形 C、六边形 D、七边形
6、设实数x,
y满足条件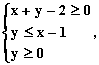
则 
的取值范围是
（ ）
A、
B、 
C、
D、 
7、方程
与
的曲线在同一坐标系中的图象可能是
（ ）
8、椭圆
的焦点是
、
，在椭圆上求一点P，使它满足
，则下面结论正确的是
（ ）
A、点P一定存在 B、点P一定不存在 C、欲求点P还需条件 D、以上结论都不对
9、已知m、n是不同的直线，α、β是不同的平面，有下列四个命题：
①若m
α，n∥α，则m∥n； ②若
，则
、
是异面直线；
③若m⊥α，m⊥β，则α∥β；④若α∩β=n，m∥n，则m∥α且m∥β.
其中真命题的个数是 （ ）
A、0 B、1 C、2 D、3
10、已知正方体ABCD－A1B1C1D1的棱长为1，点P是平面ABCD内的动点，若点P到直线
的距离等于点P到直线CD的距离，则动点P的轨迹所在的曲线是
（ ）
A、直线 B、椭圆 C、抛物线 D、双曲线
二、填空题（本大题共5小题， 每小题4分，共20分）
11、直线
：
与直线
：
的夹角是___
_ ___
12、若双曲线的渐近线互相垂直，且过点
的双曲线的标准方程是
13、求到两定点A(1, 0，1)，B(3，
, 
) 距离相等的点P（x，y，z）所满足的轨迹方程是
14、瑞安中学接到国际小行星中心通报，中国科学院紫金山天文台于1981年10月23日发现的、国际编号为（4073）号小行星已荣获国际小行星中心和国际小行星命名委员会批准，正式命名为“瑞安中学星” ，这为瑞安中学110年校庆献上了一份特殊厚礼.已知它的运行轨道是以日心（太阳的中心）F为一个焦点的椭圆，测得轨道的近日点A距太阳中心2.46天文单位，远日点B距太阳中心3.54天文单位，并且F、A、B在同一直线上，则瑞安中学星运行轨道的离心率为
15、如图所示，平面
平面
，A、C
，B、D，点E、F分别在异面直线AB、CD上移动，则图中满足条件
时，有EF
.（填上你认为正确的一种条件即可，不必考虑所有情况）
三、解答题(本大题共4小题，共40分)
16、（本小题满分8分）
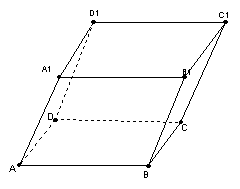如图，平行六面体
中，设
，
，
，E、F分别是BC、
的中点.
（Ⅰ）试用基底{
，
，
}表示向量
；
（Ⅱ）求证：四边形
为平行四边形.
17、（本小题满分8分）
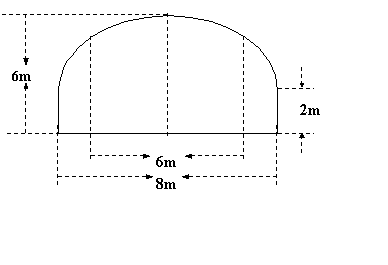
有一隧道内设双行线公路，其断截面由一个长方形和一段抛物线构成，如图所示.为确保车辆在行车道内都能安全通行，要求行驶车辆顶部（设顶部为平顶）与隧道内壁在竖直方向高度之差至少要有0.5米，若行车道总宽度AB为6米，隧道宽为8米，隧道顶部到地面的距离为6米，那么通过隧道的车辆的高度应限制为多少米？
18、（本小题满分12分）
|
|
，PA⊥面ABCD，且AB=1，AD=1，CD=2，PA=3，E为PD的中点
（Ⅰ）求证：AE//面PBC.
|
|
（Ⅱ）求直线AC与PB所成角的余弦值；
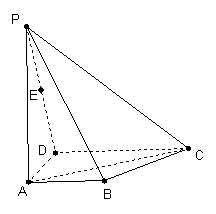（Ⅲ）在面PAB内能否找一点N，使NE⊥面PAC. 若存在，找出并证明；若不存在，请说明理由.
|
|
19、（本题满分12分）
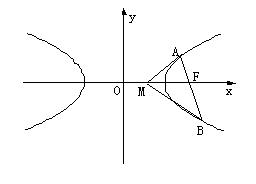
如图，过双曲线
的右焦点F任作一条与两坐标轴都不垂直的弦AB，若在
轴上的点M，且使得MF为
的一条内角平分线，则称点M为该双曲线的“右特征点”
（Ⅰ）证明：点M
是双曲线
的“右特征点”；
（Ⅱ）试根据（Ⅰ）中的结论猜测：在轴上怎样的点M是双曲线
的“右特征点”，并证明你的结论.
答案
一、选择题：1—5：DCCDC 6—10： CABBD （理科）
1—5：DBCCA 6—10： CCCBB （文科）
二、填空题：11、
12、
13、
14、0.18 15、
（答案不唯一）
三、解答题：
17、解：
（I）
，， ，且E、F分别是BC、的中点
…4分
（II）
，
所以，四边形为平行四边形. …8分
18、解：
如图建系，设隧道顶部抛物线型方程为
， …1分
由题意，将点
代入方程，得 p=2 
…3分
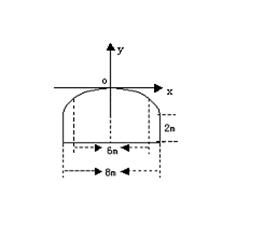设此时行车道上面宽为CD，则D（3，y）,
由
得
…5分
若在两侧车顶部和抛物线在竖直方向上高度之差
少于0.5米时，车可能会有危险；
所以通过隧道车辆的高度应限制为
米
…7分
答：通过隧道车辆的高度应不高于3.25米. …8分
19、解：（Ⅰ）取PC中点为F，连结EF，BF
又E为PD的中点，所以
且
所以EF//AB，且EF=AB，所以ABFE为平行四边形 …2分
所以AE//BF， 因为AE
面PBC， 所以AE//面PBC
…4分
（Ⅱ）建立如图所示的空间直角坐标系，
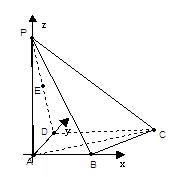则A、B、C、D、P、E的坐标分别为A（0，0，0），
B（1，0，0），C（2，1，0），D（0，1，0），
P（0，0，3），E（0，
，
）
…5分
从而
=（2，1，0），
=（1，0，
）
设与的夹角为
，则
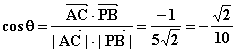， …7分
∴AC与PB所成角的余弦值为
…8分
（Ⅲ）法1：由于N点在面PAB内，故可设N点坐标为（x，0，z），
则
由NE⊥面PAC可得：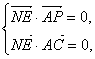
…10分
即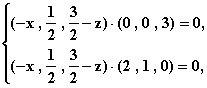
化简得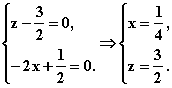
即N点的坐标为（
，0，）
所以在面PAB内存在点N（，0，），使NE⊥面PAC.
…12分
（Ⅲ）法2：在面ABCD内过D作AC的垂线交AB于G，连PG，
设N为PG的中点，连NE，则NE//DG， …10分
∵DG⊥AC，DG⊥PA，∴DG⊥面PAC 从而NE⊥面PAC
…12分
20、（理科）解：（Ⅰ）由已知得，双曲线的右焦点为
，
可设直线AB的方程为
， 代入
得
， 即
…2分
设
， 则
欲证点M是双曲线的“右特征点”；
只需证
被轴平分
即证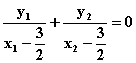 
即证
即证
…4分
因为 
因此，点M是双曲线的“右特征点”. …6分
（Ⅱ）对于双曲线
于是猜想：双曲线的右准线与轴的交点是双曲线的“右特征点”.
…8分
证明：设双曲线的右准线
与轴相交于M点，过A
B分别作的垂线，垂足分别为C
D，据双曲线的第二定义：
即
于是
，即
与
相似，
为的平分线，故M为双曲线的“右特征点”
…12分
20、（文科）解：（Ⅰ）由已知得，双曲线的右焦点为，
…1分
可设直线AB的方程为
， 代入
得 
…3分
设， 则
欲证点M是双曲线的“右特征点”；
只需证被轴平分
即证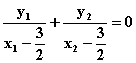
即证 即证 …6分
因为 
因此，点M是双曲线的“右特征点”.
…9分
（Ⅱ）对于双曲线
猜想：双曲线的右准线与轴的交点是双曲线的“右特征点” …12分
一．