第一学期期末考试
高二数学试卷(理)
(考试时间为120分钟,总分为160分) 2007年1月
一、选择题(每题5分,共计50分)
1.已知![]() ,则
,则![]() 的值为
的值为
A.1 B.![]() D.
D.![]()
2.设![]() ,
,![]() ,且
,且![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的图象如图所示,则导函数
的图象如图所示,则导函数![]() 的图象大致是
的图象大致是
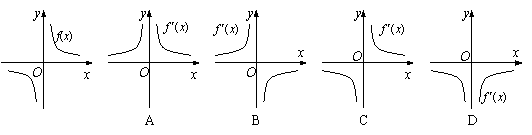
4.双曲线![]() 上的点P到点(5,
0)的距离是15, 则点P到点(-5, 0)的距离是
上的点P到点(5,
0)的距离是15, 则点P到点(-5, 0)的距离是
A.7 B.
5.已知实数x,y满足条件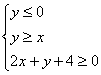 ,则z = x + 3y的最小值是
,则z = x + 3y的最小值是
A.![]() B.
B.![]() C.12 D.-12
C.12 D.-12
6.曲线![]() 与曲线
与曲线![]() 的
的
A.焦距相等 B.离心率相等 C.焦点相同 D.准线相同
7.“a>b>![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不允分也不必要条件
8.设![]() 是
是![]() 所在平面外一点,若
所在平面外一点,若![]() ,则点
,则点![]() 在这
在这
个平面上的射影是![]() 的
的
A.重心 B.垂心 C.外心 D.内心
9.删除正整数数列1,2,3,……中的所有完全平方数,得到一个新数列.这个新数列
的第2007项是
A.2050 B.
10.已知不等式![]() 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为
的最小值为
A.8
B.
二、填空题(每题5分,共计30分)
11.双曲线![]() 的渐近线方程是 ▲ .
的渐近线方程是 ▲ .
12.命题:“若![]() ,则
,则![]() 或
或![]() ”的否命题是 ▲ .
”的否命题是 ▲ .
13.等差数列的第2,3,6项顺次成等比数列,该等差数列不是常数列,则这个等比数列的公比为 ▲ .
14.设点P在抛物线![]() 上,且点P到此抛物线的焦点的距离为6,则点P的坐标
上,且点P到此抛物线的焦点的距离为6,则点P的坐标
为 ▲ .
15.在曲线![]()
![]() 上取一点M,使过M点的切线方程与直线y=
上取一点M,使过M点的切线方程与直线y=![]() x平行,则M点的坐标是点 ▲ .
x平行,则M点的坐标是点 ▲ .
16.以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为正常数,![]() ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
②双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④和定点![]() 及定直线
及定直线![]() 的距离之比为
的距离之比为![]() 的点的轨迹方程为
的点的轨迹方程为![]() .
.
其中真命题的序号为 ▲ .
三、解答题(共计80分)
17.(本题满分14分)已知抛物线![]() 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线![]() :
:![]() 的一个焦点
的一个焦点![]() 且垂直于
且垂直于![]() 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求抛物线![]() 的方程及其焦点
的方程及其焦点![]() 的坐标;
的坐标;
(2)求双曲线![]() 的方程及其离心率
的方程及其离心率![]() .
.
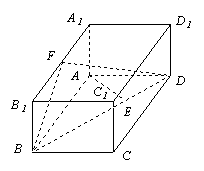
 18.(本题满分16分)如图,已知长方体
18.(本题满分16分)如图,已知长方体
![]() 中,
中,![]() ,
,![]() ,直
,直
线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() 垂直
垂直
![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
19.(本小题满分16分)已知数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() ).
).
(Ⅰ)若![]() = 30,求
= 30,求![]() ;
;
(Ⅱ)试写出a30关于![]() 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得![]() 是公差为
是公差为![]() 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出![]() 关于
关于![]() 的关系式(
的关系式(![]() N
N![]() );
);
(Ⅳ)在(Ⅲ)条件下,且![]() ,试用
,试用![]() 表示此数列的前100项和
表示此数列的前100项和![]() .
.
20.(本小题满分16分)已知![]() 在
在![]() 与
与![]() 时,都取得极值.
时,都取得极值.
(1) 求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的单调区间和极值;
的单调区间和极值;
(3)若对![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
21.(本小题满分18分)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且![]() ,
,![]() .
.
(1)求椭圆的方程;
 (2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数
(2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数![]() ,使
,使![]() ,请给出证明.
,请给出证明.
 第一学期期末考试
第一学期期末考试
高二数学试卷答卷(理)
一、选择题(每题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每题5分,共计30分)
11. 12.
13. 14. 15. 16.
三、解答题(共计80分)
17.(本题满分14分)
 |
18.(本题满分16分)
19.(本题满分16分)
20.(本题满分16分)

 21.(本题满分18分)
21.(本题满分18分)
第一学期期末考试
高二数学试卷参考答案(理)
一、选择题(每题5分,共计50分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | C | D | D | B | A | A | B | C | C |
二、填空题(每题5分,共计30分)
11.![]() ; 12.若
; 12.若![]() ,则
,则![]() 且
且![]() ; 13.
; 13.![]()
14.![]() ;
15.
;
15.![]() ;
16.②③
;
16.②③
三、解答题(共计80分)
17.(本题满分14分)已知抛物线![]() 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线![]() :
:![]() 的一个焦点
的一个焦点![]() 且垂直于
且垂直于![]() 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求抛物线![]() 的方程及其焦点
的方程及其焦点![]() 的坐标;
的坐标;
(2)求双曲线![]() 的方程及其离心率
的方程及其离心率![]() .
.
解:(1)由题意可设抛物线![]() 的方程为
的方程为![]() .
(2分)
.
(2分)
把![]() 代入方程为
代入方程为![]() ,得
,得![]() (4分)
(4分)
因此,抛物线![]() 的方程为
的方程为![]() .
(5分)
.
(5分)
于是焦点![]() (7分)
(7分)
(2)抛物线![]() 的准线方程为
的准线方程为![]() ,
,
所以,![]() (8分)
(8分)
而双曲线![]() 的另一个焦点为
的另一个焦点为![]() ,于是
,于是
![]()
因此,![]() (10分)
(10分)
又因为![]() ,所以
,所以![]() .
.
于是,双曲线![]() 的方程为
的方程为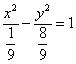 .
(12分)
.
(12分)
因此,双曲线![]() 的离心率
的离心率![]() .
(14分)
.
(14分)
 18.(本题满分16分)如图,已知长方体
18.(本题满分16分)如图,已知长方体![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]()
垂直![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
解:在长方体![]() 中,以
中,以![]()
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]()
轴,以![]() 所在的直线为
所在的直线为![]() 轴,建立如图
轴,建立如图
所示空间直角坐标系.
由已知![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() .又
.又
![]() 平面
平面![]() ,从而
,从而![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,而
,而![]() ,
,
![]() ,
,![]() ,
,![]() ,因此易得
,因此易得![]() ,
,![]() . (4分)
. (4分)
(1)因为![]() ,
,![]() ,所以
,所以
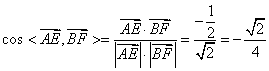 .
.
于是,异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
(10分)
.
(10分)
(2)易知直线![]() 的一个方向向量为
的一个方向向量为![]() ,设
,设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() ,由
,由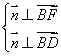
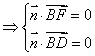
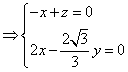
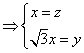
取![]() ,得
,得![]() ,所以
,所以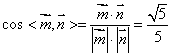 ,即直线
,即直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
(16分)
.
(16分)
19.(本小题满分16分)已知数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() ).
).
(Ⅰ)若![]() = 30,求
= 30,求![]() ;
;
(Ⅱ)试写出a30关于![]() 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得![]() 是公差为
是公差为![]() 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出![]() 关于
关于![]() 的关系式(
的关系式(![]() N
N![]() );
);
(Ⅳ)在(Ⅲ)条件下,且![]() ,试用
,试用![]() 表示此数列的前100项和
表示此数列的前100项和![]() .
.
解:(Ⅰ)![]()
![]()
于是,![]() (4分)
(4分)
(Ⅱ)![]()
![]()
![]()
因此,![]() (8分)
(8分)
(Ⅲ)![]()
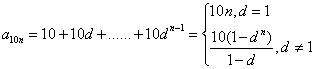 (12分)
(12分)
(Ⅳ)![]()
![]()
![]()
![]()
![]() +
+![]()
![]() (16分)
(16分)
20.(本小题满分16分)已知![]() 在
在![]() 与
与![]() 时,都取得极值.
时,都取得极值.
(1) 求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的单调区间和极值;
的单调区间和极值;
(3)若对![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(1)f ′(x)=3x2+
由题设,x=1,x=-为f ′(x)=0的解.
-a=1-,=1×(-).∴a=-,b=-2. (4分)
经检验得:这时![]() 与
与![]() 都是极值点.
(5分)
都是极值点.
(5分)
(2)f (x)=x3-x2-2 x+c,由f (-1)=-1-+2+c=,c=1.
∴f (x)=x3-x2-2 x+1.
| x | (-∞,-) | (-,1) | (1,+∞) |
| f ′(x) | + | - | + |
∴ f (x)的递增区间为(-∞,-),及(1,+∞),递减区间为(-,1).
当x=-时,f (x)有极大值,f (-)=;当x=1时,f (x)有极小值,f (1)=-.(10分)
(3)由(1)得,f ′(x)=(x-1)(3x+2),f (x)=x3-x2-2 x+c,
f (x)在[-1,-![]() 及(1,2]上递增,在(-,1)递减.
及(1,2]上递增,在(-,1)递减.
而f (-)=--++c=c+.f (2)=8-2-4+c=c+2.
∴ f (x)在[-1,2]上的最大值为c+2.
∴ ![]()
∴ ![]()
∴ 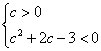 或
或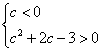
∴ ![]() 或
或![]() .
(16分)
.
(16分)
21.(本小题满分18分)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数![]() ,使
,使![]() ,请给出证明.
,请给出证明.
解:(1)![]() ,即
,即![]() ,
,![]() .
.

![]()
![]()
∴ ![]()
∴ ![]() (4分)
(4分)
如图建立直角坐标系,设椭圆的方程
为![]()
![]() .
.
则由![]() 代入
代入![]() 得
得![]() ,
,
把![]() 代入
代入![]() 得
得![]() .
.
所以椭圆的方程为![]() (8分)
(8分)
(2)设![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
由![]() 可知直线
可知直线![]() 与
与![]() 的倾斜角互补.
(10分)
的倾斜角互补.
(10分)
于是直线![]() 与
与![]() 的斜率互为相反数,因此可设:
的斜率互为相反数,因此可设:
直线![]() 的方程为
的方程为![]()
和直线![]() 的方程为
的方程为![]() .
.
由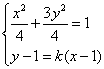 解得
解得![]() ;
(14分)
;
(14分)
同理由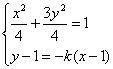 解得
解得![]() .
.
∴ 直线![]() 的斜率
的斜率![]() ,而
,而![]() (特例).
(16分)
(特例).
(16分)
∴ ![]()
∴ 总存在实数![]() ,使
,使![]() .
(18分)
.
(18分)