高二数学第一学期
数学选修1-1考试(文科)
班别_________ 姓名___________ 座号_________ 成绩__________
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题4分,共40分)。
1.已知命题甲:![]() ,命题乙:点
,命题乙:点![]() 是可导函数
是可导函数![]() 的极值点,则甲是乙的( )
的极值点,则甲是乙的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分而不必要条件
2、已知椭圆的焦点为![]() 和
和![]() ,点
,点![]() 在椭圆上的一点,且
在椭圆上的一点,且![]() 是
是![]() 的等差中项,则该椭圆的方程为(
)
的等差中项,则该椭圆的方程为(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知![]() ,点P在A、B所在的平面内运动且保持
,点P在A、B所在的平面内运动且保持![]() ,则
,则![]() 的最大值和最小值分别是 ( )
的最大值和最小值分别是 ( )
A.![]() 、3 B.10、
、3 B.10、
4、椭圆的一焦点与短轴两顶点组成一个等边三角形,则椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.双曲线x2-ay2=1的焦点坐标是 ( )
A.(![]() , 0) , (-
, 0) , (-![]() , 0) B.(
, 0) B.(![]() , 0), (-
, 0), (-![]() , 0)
, 0)
C.(-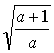 , 0),(
, 0),(![]() , 0) D.(-
, 0) D.(-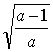 , 0), (
, 0), (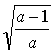 , 0)
, 0)
6、若双曲线![]() 与
与![]() 的离心率分别为
的离心率分别为![]() ,则当
,则当![]() 变化时,
变化时,![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.曲线y=x3+x-2在点P0处的切线平行于直线y=4x-1,则P0的坐标可能是( )
A.(0,1) B.(1,0) C.(-1,0) D.(1,4)
8. 函数![]() 在区间
在区间![]() 上单调递增,那么实数a的取值范围是( )
上单调递增,那么实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、方程x3-6x2+9x-10=0的实根个数是
A、3
B、
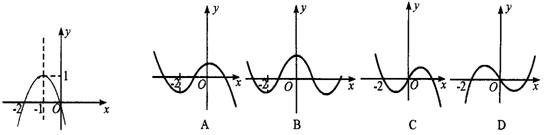
10.已知函数f(x)的导函数![]() 的图像如左图所示,那么函数f(x)的图像最有可能的是( )
的图像如左图所示,那么函数f(x)的图像最有可能的是( )
二、填空题(本大题共4小题;每小题4分,共16分。把答案填在题中横线上)
11.命题![]() 的否命题是
.
的否命题是
.
12.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的 条件。
(填“充分不必要”“必要不充分”、“充要”或“既不充分也不必要” )
13.若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4; ②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆; ④若C表是椭圆,且长轴在x轴上,则![]() .其中真命题的序号为
(把所有正确命题的序号都填在横线上)
.其中真命题的序号为
(把所有正确命题的序号都填在横线上)
14.函数y=![]() 的单调增区间是 ,减区间是 .
的单调增区间是 ,减区间是 .
一.选择题(每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题:请把答案填在题中横线上(每小题4分,共16分)。
11._______________ 12 ______________
13. ________________ 14 ______________ ______________
三、解答题:解答应写出文字说明、证明过程或演算步骤(共44分)。
15.(10分)求与椭圆![]() 有共同焦点,且过点
有共同焦点,且过点![]() 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
16.(12分)设椭圆方程为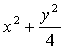 =1,过点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足![]() ,当l绕点M旋转时,求动点P的轨迹方程.
,当l绕点M旋转时,求动点P的轨迹方程.
17.(10分)设f(x)=x3-![]() x2-2x+5
x2-2x+5
(1)求函数f(x)的单调区间。
(2)求极值点与极值。
18.(12分)已知椭圆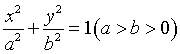 的离心率
的离心率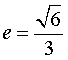 ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() 。
。
⑴求椭圆的方程;
⑵已知定点![]() ,若直线
,若直线![]() 与椭圆交于
与椭圆交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使以
的值,使以![]() 为直径的圆过
为直径的圆过![]() 点?请说明理由。
点?请说明理由。
答案:
一、 选择题 BCDAC,BCACA
二、
11 ![]()
12充分不必要 13(2)14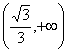
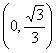
三.15.

16(1)在![]()
![]() 上为单调递增区间,在
上为单调递增区间,在![]() 上为单调递减区间.
上为单调递减区间.
(2)x=1时,y=![]() ,x=
,x=![]() 时,y=
时,y=![]()
17.解:设P(x,y)是所求轨迹上的任一点,
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
由![]() 得:(4+k2)x2+2kx-3=0, x1+x2=-
得:(4+k2)x2+2kx-3=0, x1+x2=-![]() y1+y2=
y1+y2=![]() ,
,
由![]() 得:(x,y)=
得:(x,y)=![]() (x1+x2,y1+y2),
(x1+x2,y1+y2),
即: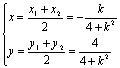
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程所以动点P的轨迹方程为:4x2+y2-y= 0。
18..
