高二数学(文科)中段试题
命题人:xyyyh2211
参考公式
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一.选择题:(每小题5分,共50分)
1.
若函数![]() 的图像上一点
的图像上一点![]() 及邻近一点
及邻近一点![]() ,则
,则![]() ( D )
( D )
A.3
B.![]() C.
C.![]() D.
D.![]()
2.曲线 ![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() , 则点
, 则点![]() 的坐标是( C )
的坐标是( C )
A.![]() B.
B.![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
3.若有一组数据的总偏差平方和为120,相关指数为0.6,则回归平方和为 ( A )
A. 72 B.
4.已知集合M={1,![]() },N={1,3},M∩N={1,3},则实数m的值为( B )
},N={1,3},M∩N={1,3},则实数m的值为( B )
A. 4
B.-
5.在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上的两个柱形高度的乘积相差越大,则两个分类变量有关系的可能性就( A )
A.越大 B.越小 C.无法判断 D.以上对不对
6. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为 ( A
)
”的结论显然是错误的,这是因为 ( A
)
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
7.函数![]() 在[0,3]上的最大值和最小值分别是( C )
在[0,3]上的最大值和最小值分别是( C )
A. 5,15 B. 5,![]() C. 5,
C. 5,![]() D. 5,
D. 5,![]()
8. 下列表述正确的是( D ).
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
A.①②③; B.②③④; C.②④⑤; D.①③⑤.
9.设复数![]() 满足条件
满足条件![]() 那么
那么![]() 的最大值是( D )
的最大值是( D )
A.3 B.![]() C.
C.![]() D.4
D.4
10.把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为( B )

二.填空题:(每小题5分,共20分)
11.复平面上的正方形的三个顶点表示的复数有三个为![]() 那么第四个顶点对应的复数是___________________
那么第四个顶点对应的复数是___________________ ![]()
12.若函数![]() 的图象与x轴相切于(1,0)点,则函数f(x)的解析式为
的图象与x轴相切于(1,0)点,则函数f(x)的解析式为![]() .
.
13.在研究身高和体重的关系时,求得相关指数![]() ______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
14. 类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长之间满足关系:![]() 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.

![]()
一、选择题(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | A | B | B | A | C | D | D | B |
二、填空题(每小题5分,共20分)
11. 12.
13.__________________________14、_
三.解答题: (共80分)
15.(13分)求函数![]() 的单调区间。
的单调区间。
解:函数![]() 的定义域为
的定义域为![]() -------------2分
-------------2分
由![]() ,得
,得![]() -----8分
-----8分
令![]() ,得
,得![]() 或
或![]() ;
;
令![]() ,得
,得![]() 或
或![]() --------------------------------12分
--------------------------------12分
所以函数![]() 的单调增区间是
的单调增区间是![]() ;
;
单调减区间是![]() -----------------13分
-----------------13分
16.(14分) 在对人们的休闲方式的一次调查中,共调查了124人,其中女
性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27
人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外
33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
解:(1)2×2的列联表
| 休闲方式 性别 | 看电视 | 运动 | 总计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 总计 | 64 | 60 | 124 |
------------------------6分
(2)假设“休闲方式与性别无关”
计算 ![]() -----------------------10分
-----------------------10分
因为![]() ,所以有理由认为假设“休闲方式与性别无关”是不合理的,
,所以有理由认为假设“休闲方式与性别无关”是不合理的,
即有97.5%的把握认为“休闲方式与性别有关” -----------------------------14分
17.(14分)18.(14分)己知下列三个方程: x2+4ax
证明: 假设没有一个方程有实数根,则:
| ||||
-----------------------5分
解之得: ![]() <a<-1
----------------------12分
<a<-1
----------------------12分
![]()
![]() 故三个方程至少有一个方程有实根的a的取值范围是: a a≥-1或a≤
故三个方程至少有一个方程有实根的a的取值范围是: a a≥-1或a≤![]()
-------------------14分
18.(14分)一条长为a的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
解:设两段铁丝的长度分别为x,a-x,则这两个正方形的边长分别为![]()
![]()
--------------------2分
两个正方形的面积和为S=f(x)=![]() +
+![]() =
=![]() ,0<x<a.
,0<x<a.
-----------------6分
令f’(x)=0, 即4x![]() ---------------8分
---------------8分
当x∈(0, ![]() )时, f’(x)<0, f(x)是减函数;
)时, f’(x)<0, f(x)是减函数;
当x∈(![]() ,a),f’(x)>0, f(x)是增函数; ----------------12分
,a),f’(x)>0, f(x)是增函数; ----------------12分
故x=![]() 是函数f(x)的唯一极小值点,也就是最小值点.所以当x=
是函数f(x)的唯一极小值点,也就是最小值点.所以当x=![]() ,即两段长度分别是
,即两段长度分别是![]() 时,两个正方形的面积和最小. ----------------14分19.(13分)已知
时,两个正方形的面积和最小. ----------------14分19.(13分)已知![]() 且
且![]() ,试用导数证明不等式:
,试用导数证明不等式:![]() .
.
证明:设![]() --------------------------3分
--------------------------3分
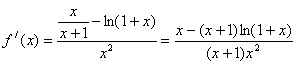
![]() -------------------------------6分
-------------------------------6分
∵![]() 且
且![]() ,∴
,∴![]() ∴
∴![]() ∴
∴![]() ----------------8分
----------------8分
∴![]() 在
在![]() 上单调递减
---------------------10分
上单调递减
---------------------10分
又∵![]() 且
且![]() ∴
∴![]() 即
即![]() ---------12分
---------12分
∴![]() ----------------------------------13分
----------------------------------13分
20.(12分)函数![]() 在
在![]() 与
与![]() 上单调性相同,在
上单调性相同,在![]() 与
与![]() 上单调性相反。(1)求c的值;(2)当
上单调性相反。(1)求c的值;(2)当![]() 为何值时,
为何值时,![]() 取得极值?并判断出这些极值点的横坐标与2、4的大小关系;(3)
取得极值?并判断出这些极值点的横坐标与2、4的大小关系;(3)![]() 的图象上是否存在点
的图象上是否存在点![]() 使f(x)在
使f(x)在![]() 处的切线斜率为
处的切线斜率为![]() ?
?
解:(1)由题意知,![]() 在
在![]() 与
与![]() 上单调性相反,
上单调性相反,![]() 在
在![]() 处取得极值,
处取得极值,![]() ,而
,而![]()
![]() -----------------3分
-----------------3分
(2)由(1)知,![]() ,若
,若![]() ,则
,则![]() ,则
,则![]() 至多有两个单调区间,不合题意;
至多有两个单调区间,不合题意;![]() 且由
且由![]() 得到
得到![]() 或
或![]() ;若
;若![]() ,则
,则![]() 在
在![]() 与
与![]() 上同号,
上同号,![]() 在
在![]() 与
与![]() 上单调性相同,不合题意;
上单调性相同,不合题意;![]() 且
且![]() 在
在![]() 的左右两侧异号,
的左右两侧异号,![]() 在
在![]() 处取得极值.
处取得极值.
![]() 在
在![]() 的左右两侧异号,
的左右两侧异号,![]() 在
在![]() 处取得极值又
处取得极值又![]() 在
在![]() 与
与![]() 上单调性相反,
上单调性相反,![]() 必有一个极值点在
必有一个极值点在![]() 内
内![]() 当
当![]() 或
或![]() 时,
时,![]() 取得极值且
取得极值且![]() ----------------------8分
----------------------8分
(3)假设![]() 的图象上存在一点
的图象上存在一点![]() 使
使![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]() ,则
,则![]() ∴关于
∴关于![]() 的方程
的方程![]() 有解,∴
有解,∴![]()
∴![]() 又由(2)知,
又由(2)知,![]() ,矛盾.
,矛盾.
∴假设不成立,从而不存在点![]() 使题设成立.
-------------------12分
使题设成立.
-------------------12分