高二上期数学期末复习题

一、选择题：

1．由条件a<b<0得出下面四个不同的结论①②③④.则其中正确的结论有　（　　 ）　　　　　　　　　　　　

A．4个　　　　　 B．3个　　　　  C．2个　　　　  D．1个

2．直线与y轴的夹角等于（　　 ）

A．　　　　　  B．　　　　　 C．　　　　 D．

3．直线ax+(1-a)y=3与直线(a-1)x+(2a+3)y=2互相垂直，则a的取值为（　　 ）

A．-3　　　　　  B． 1　　　　　  C．0或　　 D．1或-3

4．与直线3x-4y+5=0关于y轴对称的直线方程为（　　　 ）

A．3x+4y-5=0　　B．3x+4y+5=0　　C．3x-4y-5=0　　D．3x-4y+5=0

5．过点（1，2）且与原点距离最大的直线方程是 （　　　　 ）

A．x–2y+3=0　　 B．2x+y–4=0　　C．x+3y–7=0　　　D．x+2y–5=0

6．已知三角形ABC的顶点A（2，4），B（-1，2），C（1，0），点P（x，y）在三角形内部及其边界上运动，则Z=x-y的最大值和最小值分别是 （　　　　）　　　　　　　　　 

A．3，1　　　　B．1，-3　　　　C．-1，-3　　　　  D．3，-1

7．已知动点P到F₁(-5,0)的距离与它到F₂(5,0)的距离之差等于6,则P的轨迹方程是（　）

A.　　　　　　　　　 B.　　

C. (x≤-3)　　　　　 D. (x≥3)

8．曲线的离心率为（　　 ）

A.　　　　  B.　　　　　　 C.　　　　　 D.

9．已知、是椭圆的左右焦点，M为椭圆上任意一点，则的最大值为（　　　　 ）

A． a 　　　　　B． b　　　　 C． 　　　　D．

10．在下列函数中，当取正数时，最小值为2的是（　　　）

A. B. C．　　 D．

11．已知A(-3,8)和B(2,2), 在x轴上有一点M，使AM+BM最短，那么点M的坐标是

A．(-1,0)　　　　  B．(1,0)　　　　C．(,0)　　　　D． (0, )

12．抛物线上有一点P，P到椭圆的左顶点的距离的最小值为（　　　　）

A．　　　 B．2+　　　 　　　 C．　　　　 D．

二、填空题：

13．不等式的解集是　　　　

14．以坐标原点为顶点，圆的圆心为焦点的抛物线方程是　　   

15．已知，则的最小值为　　　　　　

16．已知椭圆中过点M（，）的弦被点M平分，求这条弦所在直线的斜率是__________________

三、解答题：

17．解不等式：（1）；　（2）

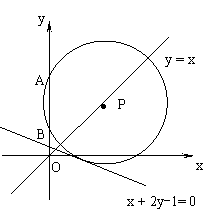18．圆心P在直线y = x上，且与直线x + 2y-1= 0相切的圆，截y轴的上半轴所得的弦　　AB长为2，如图所示，求此圆的方程。

19．若点P到定点F（4，0）的距离比它到直线x+5=0的距离小1，

（1）求点P的轨迹方程；

（2）已知点A（2，4），为使取得最小值，求点P的坐标及的最小值。

20．求两条渐近线为且截直线所得弦长为的双曲线方程。

21．设，两点在抛物线上，是AB的垂直平分线。

（Ⅰ）当且仅当取何值时，直线经过抛物线的焦点F？

（Ⅱ）当直线的斜率为2时，求在轴上截距的取值范围。

22．,(a>0)是x轴上两定点，动点M在x轴上的射影为N且满足条件：(m≠0)

(1)求动点M的轨迹C的方程，并说明轨迹是什么曲线？

(2)当时,过点F的直线与动点M的轨迹C相交于G,K两点,求证:.

参考答案：

ABDAD　 BDACD　 BA

13、　 14、　 15、　　16、

17、解：原不等式等价为，即

　　由①得：-6<x<3；由②得：x<-2或x>-1　　

所以原不等式的解集为{x-6<x<-2或-1<x<3}

18、解：∵圆心P在直线y = x上，∴可设P的坐标为（k，k），

　　作PQ⊥AB于Q，连接AP，在Rt△APQ中，AQ=1，AP=r，PQ=k

　　∴r=　　　　　　　　　　 

　　又r=点P到直线x + 2y-1= 0的距离

　　∴　　　　　　　

　　整理，得

　　解得，k=2或（舍去）　　　　

　  ∵所求圆的半径为=　　

　　∴所求圆的方程为：

19、解：(1)设P（x,y）,则点P到定点F（4，0）的距离是，它到直线x+5=0的距离是　　

所以 =-1　 化简得，　因此点P的轨迹方程是　　　　

（2）由（1）得，抛物线的准线方程是x=-4。

设P到准线的距离为d，由抛物线的定义知，

=　　　　　　　　　 

从A点向准线作垂线交抛物线于P，

那么它使最小，最小值是A点到准线的距离6

因此P点的纵坐标是4，代入抛物线方程得它的横坐标是1　

所以点P的坐标（1，4），的最小值是6　

20、解:设双曲线方程为x2-4y2=.

联立方程组得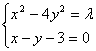，消去y得，

设直线被双曲线截得的弦为AB，且、，那么：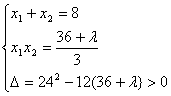

那么：AB===

解得：λ=4,所以，所求双曲线方程是：

21、解：（Ⅰ）两点到抛物线的准线的距离相等，

 ∵抛物线的准线是轴的平行线，，依题意不同时为0

∴上述条件等价于

∵

∴上述条件等价于即当且仅当时，经过抛物线的焦点。

（Ⅱ）设在轴上的截距为，依题意得的方程为；过点的直线方程可写为，所以满足方程

　　　　得

　为抛物线上不同的两点等价于上述方程的判别式，即

设的中点的坐标为，则

，

由，得，于是

即得在轴上截距的取值范围为

22、解:(1)设动点M的坐标为(x,y),则有

N(x,0),　　　　　

由得

∴M的轨迹方程为　 (4分)　　　

即

①　　 当m=1时表示圆.

②　　 当m>1或0<m<1时表示椭圆.

③当m<0时表示双曲线.　　　　　　　　　　　　  (7分)

(2)当时,M的轨迹方程为

令则c>0,　F(c,0)　 设　　

当直线的斜率不存在时, 为: x=c, 代入得

∴　　　　　　　　　 (10分)

当直线的斜率存在时,设为k,则为y=k(x-c)

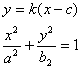由{得

∴　

由椭圆第二定义知

　　  （14分）