高二数学上期六校联考期末考试（文）
命题 合川中学
(本试卷分为第Ⅰ卷和第Ⅱ卷两部分，考试时间120分钟，满分150分)
第Ⅰ卷 (选择题 共60分)
一、 选择题 (本大题有12个小题，每小题5分，共60分) 以下每小题都给出代号为A、B、C、D的四个答案，其中只有一个答案是正确的，请将正确答案的代号涂在机读卡上相应的位置.
1、下列四个命题：
① 若
, ② 若
,
③ 若
, ④ 若
,
其中正确命题的个数有 （ ）
A、1个 B、2个 C、3个 D、4个.
2、设函数
,若
，则
、
、
的大小关系为
（ ）
A、
B、
C、
D、
.
3、已知不等式组
的解集为
，则实数
的取值范围为
（
）
A、
B、
C、
D、
.
4、已知过两点
的直线的倾斜角为
，则实数
的值为
（ ）
A、2 B、
D、0.
5、以
两点为端点的线段的垂直平分线的方程是 （ ）
A、
B、
C、
D、
.
6、已知点
，点在坐标轴上，若
，则这样的点的个数为
（ ）
A、1个 B、2个 C、3个 D、4个.
7、已知两直线：
互相平行，则它们之间的距离为（ ）
A、4 B、
C、
D、
.
8、已知双曲线
两条渐近线的夹角为
，则双曲线的离心率为（ ）
A、
B、
C、
D、2 .
9、椭圆
交于
两点，
为
中点，
为坐标原点，若直线
的斜率为
，则
的值为
（ ）
A、
B、 
C、
D、
.
10、抛物线顶点在原点，焦点在
轴上，抛物线上的点
到焦点的距离为4，则的值为
（ ）
A、4 B、
C、4 或 
D、2 或 .
11、椭圆
的两个焦点分别为
，它与双曲线
的一个交点为，则
的值为
（ ）
A、
B、
C、
D、
.
12、关于曲线
，下列四个命题：
①曲线
不可能是圆,
②若曲线是椭圆，则有
,
③若曲线是双曲线，则
,
④若曲线是焦点在
轴上的椭圆，则
,
其中正确命题的个数为 （ ）
A、4个 B、3个 C、2个 D、1个.
第II卷 (非选择题 共90分)
二、填空题（本大题有4个小题，每小题4分，共16分）请把答案填在答题卷上相应的位置.
13、已知实数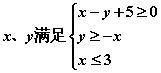
，则代数式
的最大值为________.
14、不等式
的解集为
，则实数的值为_______.
15、已知
，则
的最小值为________.
16、等腰三角形一腰所在直线的方程为
，底边所在直线方程为
,点
在另一腰上，则这条腰所在直线方程为___（以直线方程的一般式作答）.
三、解答题（本大题有6个小题，共74分）解答应写出必要的文字说明、证明过程或演算步骤.
17、(本小题满分13分)
已知函数
，函数
的图象与
的图象关于原点对称.
① 求的解析式；
② 解关于的不等式：
.
18、(本小题满分13分)
已知圆过
两点，圆心在直线
上，求此圆的方程.
19、(本小题满分12分)
已知椭圆中心在原点，长轴在轴上，其离心率为
，原点
关于直线
的对称点落在椭圆的左准线上 .
① 求椭圆方程 ；
② 设直线
与椭圆交于
两点，求
的面积 .
20、(本小题满分12分)
设点是抛物线
上异于原点的一点，过点作抛物线的切线交
于点. 当点在抛物线上运动时，求线段中点的轨迹方程.
21、(本小题满分12分)
已知双曲线中心在原点，虚轴长
，相应于焦点
的准线
与轴交于点
，且
，过点
作不垂直于轴的直线交双曲线于
两点.
① 求双曲线方程；
② 求证：
为定值.
22、(本小题满分12分)
已知椭圆
：
与双曲线
：
，若椭圆的一条准线方程为
，双曲线的一条渐近线方程为
.
① 求椭圆与双曲线的方程；
②
设椭圆的左、右顶点分别为，过点作倾斜角为锐角的直线交双曲线于点(
)，交椭圆于点，点恰为
中点，延长
交椭圆于另一点
.
求证：
.
高二数学上期六校联考期末考试
数学答题卷
二、填空题：（本大题有4个小题，每小题4分，共16分）
| 评分人 |
|
| 得 分 |
|
13．____________.14．__________.
15．____________.16．__________.
三、解答题：（本大题有6个小题，共74分）请大家一定要看清题号，在每题规定的地方答题，不要答错了地方，否则一律不给分.
| 评分人 |
|
| 得 分 |
|
17(本小题满分13分)
解：
| 评分人 |
|
| 得 分 |
|
18. (本小题满分13分)
解：
| 评分人 |
|
| 得 分 |
|
19. (本小题满分12分)
解：
| 评分人 |
|
| 得 分 |
|
20. (本小题满分12分)
解：
| 评分人 |
|
| 得 分 |
|
21. (本小题满分12分)
解：
| 评分人 |
|
| 得 分 |
|
22. (本小题满分12分)
解：