二面角的基本求法例题及练习

一、平面与平面的垂直关系

1．判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

例1．在空间四边形ABCD中，AB=CB，AD=CD，E、F、G分别是AD、DC、CA的中点。

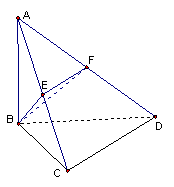　　 求证：。

例2．，，E、F分别是AC、AD的中点。

　　 求证： 。

2．性质定理：若两个平面互相垂直，则在一个平面内垂直于它们交线的直线垂直于另一个平面。

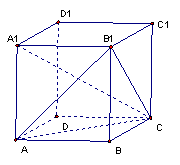
例3．在正方体ABCD—A₁B₁C₁D₁中，求A₁B和平面A₁B₁CD所成的角.。

二、二面角的基本求法

1．定义法：在棱上取点，分别在两面内引两条射线与棱垂直。

例4．在正方体ABCD—A₁B₁C₁D₁中，

　 求（1）二面角的大小；

　　 （2）平面与平面所成角的正切值。

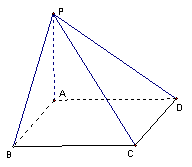
练习：过正方形ABCD的顶点A作，设PA=AB=，

求二面角的大小。

2．三垂线法

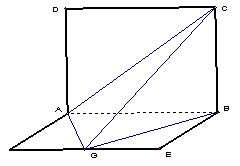例5．是正方形，ABEF是矩形且AF=AD=，G是EF的中点，

（1）求证：；

（2）求GB与平面AGC所成角的正弦值；

（3）求二面角的大小。

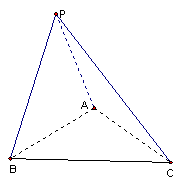例6．点P在平面ABC外，是等腰直角三角形，，是正三角形，。

（1）求证：；

（2）求二面角的大小。

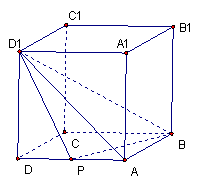
练习：正方体ABCD—A₁B₁C₁D₁的棱长为1，P是AD的中点，求二面角的大小。

3．垂面法

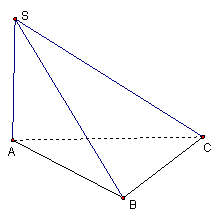
例7．，

　　（1）求证：；

（2）求二面角的大小；

（3）求异面直线SC与AB所成角的余弦值。

4．无棱二面角的处理方法

（1）找棱

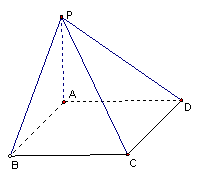例8．过正方形ABCD的顶点A作，设PA=AB=，

　　 求平面PAB与平面PCD所成二面角的大小。

（2）射影面积法（）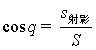

例9．正方体ABCD—A₁B₁C₁D₁的棱长为1，P是棱的中点，

　　 求平面与平面ABCD所成二面角的大小。