单元检测题(§9.1～§9.6)
班级：___________姓名：___________
一、选择题(本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1.如果a和b是异面直线，AB是它们的公垂线，直线c∥AB，那么c与a和b这两条直线交点的个数是（ ）
A.0 B.1
C.最多1个 D.最多2个
2.若两个平面互相垂直，在第一个平面内的一条直线a垂直于第二个平面内的一条直线b，那么（ ）
A.直线a垂直于第二个平面
B.直线b垂直于第一个平面
C.直线a不一定垂直于第二个平面
D.过a的平面必垂直于过b的平面
3.四棱锥S—ABCD的底面ABCD是矩形，SA⊥底面ABCD，则这个四棱锥中，互相垂直且异面的棱的对数为（ ）
A.2 B.3
C.4 D.5
4.空间四边形ABCD中，M、N分别是AB、CD的中点，AC、BD是空间四边形的对角线，那么有（ ）
A.MN＝
（AC＋BD） B.MN＞（AC＋BD）
C.MN＜（AC＋BD） D.以上三种情况都有可能
5.已知a、b是空间两条异面直线，它们所成的角为80°,过空间任一点作直线l,使l与a,b所成角均为50°,这样的l有___________条.（ ）
A.1 B.2
C.3 D.4
6.PA、PB、PC是从P点引出的三条射线，每两条的夹角都是60°，则直线PC与平面APB所成的角的余弦值是（ ）
A B.
C.
D.
7.矩形ABCD，已知AB＝AD，E是AD的中点，沿BE将△ABE折起到△A′BE的位置，使A′C＝A′D，则A′C与平面BEDC所成角的正切值是（ ）
A.2 B.
C.
D.
8.设α、β 表示平面，a表示直线，且直线a不在平面α或β 内，并有①α∥β ；
②a⊥α；③a⊥β .以其中任意两个为条件，另一个为结论，可构造出三个命题，其中正确命题的个数是（ ）
A.1 B.2
C.3 D.0
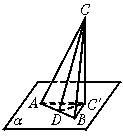
9.如图，AB是圆的直径，C是圆周上一点，PC垂直于圆所在平面，若BC=1，AC=2，PC=1，则P到直线AB的距离为（ ）
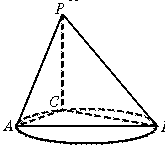
A.1 B.2
C.
D.
10.平面α∩平面β =CD,P为这两个平面外一点，PA⊥α于A，PB⊥β 于B，若PA=2，PB=1，AB=
，则二面角α—CD—β 的大小为（ ）
A.150° B.120°
C.90° D.60°
二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)
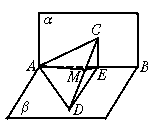
11.如图，∠BAD=90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直，E是BC的中点，则AE与平面BCD所成角的大小为___________.
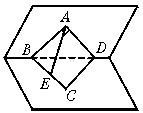
12.平面α∥平面β ，它们之间的距离是８，点A、D∈α，点B∈β ，点C是点D在β 上的射影，且AD＝20，AB＝10，则BC的最大值是__________.
13.把等腰直角三角形ABC沿斜边BC上的高线AD折成一个二面角，此时∠BAC=60°,那么此二面角的大小为___________.
14.已知下列命题：
①两两相交的三条直线确定一个平面；
②过平面外一点，有且仅有一个平面与这个平面垂直；
③平面α内不共线的三点到平面β 的距离相等，则α∥β ；
④两个平面互相垂直，过其中一个平面内一点作它们的交线的垂线，则此直线垂直于另一个平面；
⑤过两异面直线外一点，有且仅有一个平面与这两异面直线平行.
其中错误的命题序号是__________.
三、解答题(本大题共4小题，共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题10分)
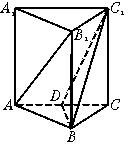
已知正三棱柱ABC—A1B1C1的底面边长为8，侧棱长为6，D为AC的中点.
(1)求证AB1∥平面C1DB；
(2)求异面直线AB1与BC1所成角的余弦值.
16.(本小题10分)
Rt△ABC的斜边AB在平面α内，AC、BC与平面α所成角分别为30°和45°，求
△ABC所在平面与α所成的锐二面角.
17.(本小题12分)
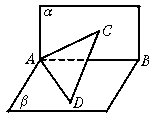
已知：直二面角α—AB—β ，点C∈α，点D∈β ，且∠BAC＝45°，∠BAD＝60°.求：
(1)∠CAD的余弦值；
(2)直线AB与平面CAD所成角的正弦值.
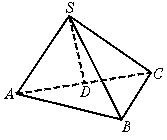
18.(本小题12分)
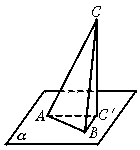
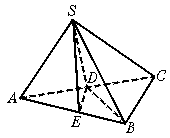
如图，Rt△ABC所在平面外一点S，且SA=SB=SC.
（1）求证：点S与斜边AC中点D的连线SD⊥面ABC；
（2）若直角边BA=BC，求证：BD⊥面SAC.
参 考 答 案
一、1．C 2．C 3．C 4．C 5．C 6．C 7.B 8.C 9.D 10.D
二、11.45° 12.26 13.90° 14.①②③④⑤
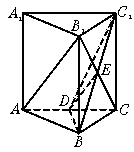
三、15.(1)证明：连结B1C交BC1于E
∵三棱柱ABC—A1B1C1是正三棱柱
∴侧面BCC1B1是矩形，
则E是B1C的中点，连结DE
∵D是AC中点，∴DE∥AB1
又 DE
平面BDC1，AB1
平面BDC1，
∴AB1∥平面BC1D
(2)解：∵三棱柱ABC—A1B
∴侧面A1ACC1⊥底面ABC
又D是AC的中点，则BD⊥AC
∴BD⊥侧面A1ACC1
而C1D平面A1ACC1，∴BD⊥DC1
则在Rt△BDC1中，BD＝，AC＝4
，BC1＝
＝10，
DE＝BE＝BC1＝5
又由（1）知，DE∥AB1，则∠DEB就是异面直线AB1与BC1所成的角
在△DEB中，有cosDEB＝
∴AB1与BC1所成角余弦值为
.
16.解：作CC′⊥面α,C′为垂足，作C′D⊥AB，连结CD.
∴CD⊥AB,∴∠CDC′是所求二面角的平面角.
由CC′⊥α可知∠CAC′=30°，∠CBC′=45°，设CC′=h，
在Rt△CC′A和Rt△CC′B中，
AC=2h，BC=
h，又AC⊥BC，
∴AB=
,
CD=(AC·BC):AB=
h
∴sinCDC′=
且∠CDC′为锐角，
∴∠CDC′=60°
∴△ABC所在平面与α所成的二面角为60°
17.解：(1)作CE⊥AB于E，作ED⊥AD于D，连CD
∵二面角α—AB—β 是直二面角
∴CE⊥平面β
又∵DE⊥AD，∴AD⊥CD
则cosCAD＝
·
＝cosDAE·cosCAE＝
．
（2）作EM⊥CD于M，连AM
∵AD⊥CD，AD⊥DE，
∴AD⊥平面CED
∴平面ACD⊥平面ECD
而EM平面CDE，
∴EM⊥平面ACD
∠EAM就是AB与平面CAD所成的角
设AE＝1，则DE＝，CE＝1
∴ME＝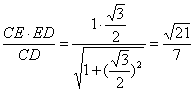
∴sinEAM＝
∴直线AB与平面CAD所成角的正弦值为
18.证明：（1）取AB中点E，连结DE、SE，则
DE⊥AB
又SA=SB，∴SE⊥AB
∴AB⊥面SED，∴AB⊥SD，
又SA=SC，∴SD⊥AC，
∴SD⊥面ABC
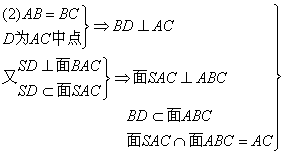
BD⊥面SAC