二次函数、二次方程及二次不等式的关系
重难点归纳
1
二次函数的基本性质
(1)二次函数的三种表示法
y=ax2+bx+c;y=a(x－x1)(x－x2);y=a(x－x0)2+n
(2)当a>0,f(x)在区间［p,q］上的最大值M，最小值m,令x0=
(p+q)
若－
<p,则f(p)=m,f(q)=M;
若p≤－<x0,则f(－)=m,f(q)=M;
若x0≤－<q,则f(p)=M,f(－)=m;
若－≥q,则f(p)=M,f(q)=m
2
二次方程f(x)=ax2+bx+c=0的实根分布及条件
(1)方程f(x)=0的两根中一根比r大，另一根比r小
a·f(r)<0;
(2)二次方程f(x)=0的两根都大于r
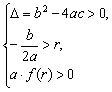
(3)二次方程f(x)=0在区间(p,q)内有两根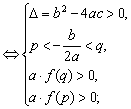
(4)二次方程f(x)=0在区间(p,q)内只有一根f(p)·f(q)<0,或f(p)=0(检验)或f(q)=0(检验)检验另一根若在(p,q)内成立
(5)方程f(x)=0两根的一根大于p,另一根小于q(p<q)
3
二次不等式转化策略
(1)二次不等式f(x)=ax2+bx+c≤0的解集是
(－∞,α
)∪［β,+∞
a<0且f(α)=f(β)=0;
(2)当a>0时，f(α)<f(β) α+<β+,
当a<0时，f(α)<f(β)α+>β+;
(3)当a>0时，二次不等式f(x)>0在［p,q］恒成立
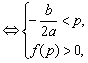或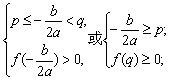
(4)f(x)>0恒成立
典型题例示范讲解
例1已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证两函数的图象交于不同的两点A、B；
(2)求线段AB在x轴上的射影A1B1的长的取值范围
命题意图
本题主要考查考生对函数中函数与方程思想的运用能力
知识依托
解答本题的闪光点是熟练应用方程的知识来解决问题及数与形的完美结合
错解分析
由于此题表面上重在“形”，因而本题难点就是一些考生可能走入误区，老是想在“形”上找解问题的突破口，而忽略了“数”
技巧与方法
利用方程思想巧妙转化
(1)证明由
消去y得ax2+2bx+c=0
Δ=4b2－
c2］
∵a+b+c=0,a>b>c,∴a>0,c<0
∴
c2>0,∴Δ>0,即两函数的图象交于不同的两点
(2)解设方程ax2+bx+c=0的两根为x1和x2,则x1+x2=－
,x1x2=
A1B12=(x1－x2)2=(x1+x2)2－4x1x2
∵a>b>c,a+b+c=0,a>0,c<0
∴a>－a－c>c,解得∈(－2,－)
∵
的对称轴方程是
∈(－2,－)时，为减函数
∴A1B12∈(3,12),故A1B1∈(
)
例2已知关于x的二次方程x2+2mx+
(1)若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，求m的范围
(2)若方程两根均在区间(0，1)内，求m的范围
命题意图
本题重点考查方程的根的分布问题
知识依托
解答本题的闪光点是熟知方程的根对于二次函数性质所具有的意义
错解分析用二次函数的性质对方程的根进行限制时，条件不严谨是解答本题的难点
技巧与方法
设出二次方程对应的函数，可画出相应的示意图，然后用函数性质加以限制
解
(1)条件说明抛物线f(x)=x2+2mx+
∴
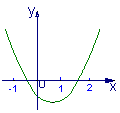
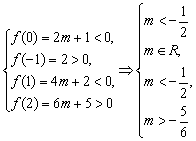
(2)据抛物线与x轴交点落在区间(0，1)内，列不等式组
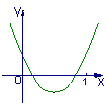
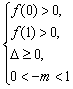
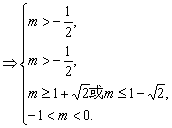
(这里0<－m<1是因为对称轴x=－m应在区间(0，1)内通过)
例3已知对于x的所有实数值，二次函数f(x)=x2－4ax+
=a－1+2的根的取值范围
解由条件知Δ≤0,即(－
≤a≤2
(1)当－≤a＜1时，原方程化为
x=－a2+a+6,∵－a2+a+6=－(a－)2+
∴a=－时，xmin=
,a=时，xmax=
∴≤x≤
(2)当1≤a≤2时，x=a2+)2－
∴当a=1时，xmin=6,当a=2时，xmax=12,∴6≤x≤12
综上所述,≤x≤12
学生巩固练习
1
若不等式(a－2)x2+2(a－2)x－4<0对一切x∈R恒成立，则a的取值范围是( )
A(－∞,2 B
－2, C(－2,2 D(－∞,－2)
2
设二次函数f(x)=x2－x+a(a>0),若f(m)<0,则f(m－1)的值为( )
A正数 B负数 C非负数 D正数、负数和零都有可能
3
已知二次函数f(x)=4x2－2(p－2)x－2p2－p+1,若在区间［－1，1］内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________
4
二次函数f(x)的二次项系数为正，且对任意实数x恒有f(2+x)=f(2－x),若f(1－2x2)<f(1+2x－x2),则x的取值范围是_________
5
已知实数t满足关系式
(a>0且a≠1)
(1)令t=ax,求y=f(x)的表达式；
(2)若x∈(0,2时，y有最小值8，求a和x的值
6
如果二次函数y=mx2+(m－3)x+1的图象与x轴的交点至少有一个在原点的右侧，试求m的取值范围
7
二次函数f(x)=px2+qx+r中实数p、q、r满足
=0,其中m>0,求证
(1)pf(
)<0;
(2)方程f(x)=0在(0，1)内恒有解
8
一个小服装厂生产某种风衣，月销售量x(件)与售价P(元/件)之间的关系为P=160－2x,生产x件的成本R=500+30x元
(1)该厂的月产量多大时，月获得的利润不少于1300元？
(2)当月产量为多少时，可获得最大利润？最大利润是多少元？
参考答案
1
解析
当a－2=0即a=2时,不等式为－4＜0,恒成立∴a=2,当a－2≠0时，则a满足
,解得－2＜a＜2,所以a的范围是－2＜a≤2
答案
C
2解析∵f(x)=x2－x+a的对称轴为x=,且f(1)>0,则f(0)>0,而f(m)＜0,∴m∈(0,1), ∴m－1＜0,∴f(m－1)>0
答案A
3
解析
只需f(1)=－2p2－3p+9>0或f(－1)=－2p2+p+1>0即－3＜p＜或－＜p＜1∴p∈(－3, )
答案
(－3，）
4
解析
由f(2+x)=f(2－x)知x=2为对称轴，由于距对称轴较近的点的纵坐标较小，
∴1－2x2－2＜1+2x－x2－2,∴－2＜x＜0
答案－2＜x＜0
5
解
(1）由loga
得logat－3=logty－3logta
由t=ax知x=logat，代入上式得x－3=
,
∴logay=x2－3x+3，即y=a
(x≠0)
(2)令u=x2－3x+3=(x－)2+
(x≠0),则y=au
①若0＜a＜1,要使y=au有最小值8，
则u=(x－)2+在(0，2上应有最大值，但u在(0，2上不存在最大值
②若a>1,要使y=au有最小值8，则u=(x－)2+,x∈(0,2应有最小值
∴当x=时，umin=,ymin=
由=8得a=16∴所求a=16,x=
6
解
∵f(0)=1>0
(1)当m＜0时，二次函数图象与x轴有两个交点且分别在y轴两侧，符合题意
(2）当m>0时，则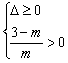
解得0＜m≤1
综上所述，m的取值范围是{mm≤1且m≠0}
7
证明
(1)
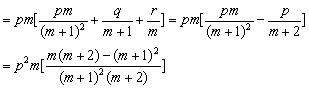
,由于f(x)是二次函数，故p≠0,又m>0,所以，pf()＜0
(2)由题意，得f(0)=r,f(1)=p+q+r
①当p＜0时，由(1）知f()＜0
若r>0,则f(0)>0,又f()＜0,所以f(x)=0在(0，)内有解;
若r≤0,则f(1)=p+q+r=p+(m+1)=(－
)+r=>0,
又f()＜0,所以f(x)=0在(,1)内有解
②当p＜0时同理可证
8
解
(1）设该厂的月获利为y,依题意得
y=(160－2x)x－(500+30x)=－2x2+130x－500
由y≥1300知－2x2+130x－500≥1300
∴x2－65x+900≤0，∴(x－20)(x－45)≤0，解得20≤x≤45
∴当月产量在20~45件之间时，月获利不少于1300元
(2）由(1）知y=－2x2+130x－500=－2(x－
)2+16125
∵x为正整数，∴x=32或33时，y取得最大值为1612元，
∴当月产量为32件或33件时，可获得最大利润1612元
课前后备注