高二下期数学巩固练习(1)
一、选择题(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | B | C | B | C | C | B | C | C |
二、填空题(每小题5分,共30分)
11、165 12、24
13、
![]() ; 14、 -
; 14、 -![]() ; 15、2; 16、 ②③ ④.
; 15、2; 16、 ②③ ④.
高二下期数学巩固练习(2)
1.(1)由已知  . (4分)
. (4分)
 (2)易知
(2)易知 ![]()
![]() ,又由(1)知
,又由(1)知![]() ,
,![]()
![]() (8分)
(8分)
|
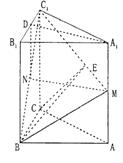
![]()
![]()
在![]() 易知
易知![]() =2,
=2,![]() ,
,![]()
![]() .(14分)
.(14分)
2.(1)每个车间的劳模派一代表介绍经验,有![]() 种选法 (3分)
种选法 (3分)
(2)若同车间的人坐在一起,有![]() 种选法
(6分)
种选法
(6分)
(3)若C车间的人不坐在一起,有![]() 144种选法
(10分)
144种选法
(10分)
(4)恰有2人坐在原位上的方法有![]() 种
(14分)
种
(14分)
3.(1)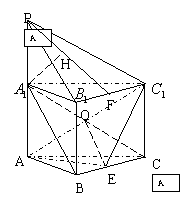

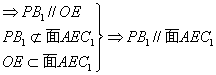 (4分)
(4分)
(2) 取![]() 中点F,连BF,易知
中点F,连BF,易知![]() ,又
,又![]()
![]()
![]()
![]()
![]() (8分)
(8分)
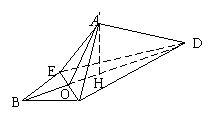
(3)连![]() ,
,![]() 为正三角形,
为正三角形,![]()
又![]()
![]() ,
,![]()
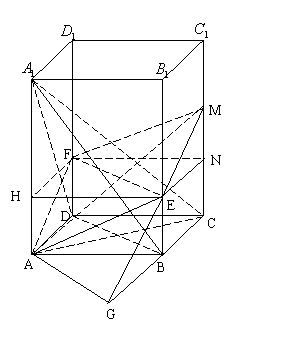 作
作 ![]()
![]() 。易由
。易由![]() 得
得![]() ,
,![]() ,又
,又![]() ,
,![]() 。 (14分)
。 (14分)
4.(1)应用三垂线定理可证得![]() ,所以
,所以![]() 面
面![]() ;(4分)
;(4分)
(2)延长ME,CB交于点G,连AG,则AG为平面AEF与平面ABD的交线,易证得AG//BD,连AC,连AM,则![]() .通
.通
过计算,
![]() .(8分)
.(8分)
(3)过EF作面ENFH//面ABCD,分别交![]() 、
、![]() 于H、N
于H、N
则![]()
![]() .
(14分)
.
(14分)
高二下期数学巩固练习(3)
AADDB BCADB
11、-10;2 12、30° 13、20 14、 1 15、32 16、 ②⑤
高二下期数学巩固练习(4)
1.解(Ⅰ)作品甲不在两端的概率![]() …5分 =
…5分 =![]() ;…6分
;…6分
(Ⅱ)作品甲、乙相邻的概率 ……11分, 作品甲、乙相邻的概率为
……11分, 作品甲、乙相邻的概率为![]() ……12分
……12分
2.解:(Ⅰ)取B1C1中点D,连结ND,A1D,
|
又,![]() 所以四边形A1MND为平行四边形,
所以四边形A1MND为平行四边形,
所以MN//A1D;…………3分
又![]() ,
,
所以MN//平面A1B1C1;…………5分
(Ⅱ)三棱柱ABC-A1B1C1为直三棱柱,所以CC1⊥BC,
又∠ACB=90°,所以BC⊥平面ACC1A1,…………7分
在平面ACC1A1上作CE⊥C1M,交C1M于点E.
则CE为BE在平面ACC1A1上的射影,
所以∠BEC为二面角B—C1M—A的平面角.………………9分
由于△CEC1与三角形C1A1M相似,所以![]() 所以
所以![]() ………11分
………11分
所以![]() ……………………12分
……………………12分
即二面角B—C1M—A的大小为![]() .…………………13分
.…………………13分
3.解:展开式中,关于x的一次项系数为![]() (3分)关于x的二次项系数为
(3分)关于x的二次项系数为![]() ,(8分)当n=5或6时,含x2项的系数取最小值25,此时m=6,n=5或 m=5,n=6. (12分)
,(8分)当n=5或6时,含x2项的系数取最小值25,此时m=6,n=5或 m=5,n=6. (12分)
4.(I)证: ![]() 三棱柱
三棱柱![]() 中
中![]() , 1分
, 1分
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 3分
3分
(II)证: ![]() 三棱柱
三棱柱![]() 中
中![]() ,
,
![]() 中
中![]()
![]() 是等腰三角形 6分
是等腰三角形 6分
![]() E是等腰
E是等腰![]() 底边
底边![]() 的中点,
的中点, ![]() 又依条件知
又依条件知![]()
且![]() 由①,②,③得
由①,②,③得![]() 平面EDB 8分
平面EDB 8分
(III)解:
![]() 平面
平面![]() ,
且
,
且![]() 不平行,
故延长
不平行,
故延长![]() ,ED后必相交,
,ED后必相交,
设交点为E,连接EF,如下图 ![]() 是所求的二面角 10分
是所求的二面角 10分
依条件易证明![]()
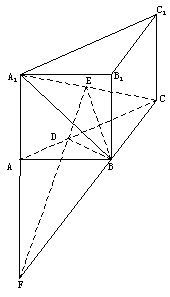
![]() 为
为![]() 中点,
中点,
![]() A为
A为![]() 中点
中点
![]()
![]()
![]() 即
即![]() 12分 又
12分 又![]() 平面EFB,
平面EFB,
![]()
![]() 是所求的二面角的平面角 13分
是所求的二面角的平面角 13分
![]() E为等腰直角三角形
E为等腰直角三角形![]() 底边中点,
底边中点,![]() 故所求的二面角的大小为
故所求的二面角的大小为![]() 14分
14分
高二下期数学巩固练习(5)
CDCCD ABA CB
11. ![]() 12. 51
13.
12. 51
13.![]() 14.
14. ![]() ; 15. 7; 16. 60°
; 15. 7; 16. 60°
高二下期数学巩固练习(6)
1.解:⑴从4名男同学中选出3人,有![]() 种方法;从6名女同学中选出4人,有
种方法;从6名女同学中选出4人,有![]() 种方法.根据分步计数原理,选出7人共有
种方法.根据分步计数原理,选出7人共有![]() 种方法.对于选出的每7个人进行全排列,有
种方法.对于选出的每7个人进行全排列,有![]() 种方法,因此所求的方法种数是:
种方法,因此所求的方法种数是:![]() 答:共有302400种排法.
答:共有302400种排法.
⑵由第⑴小题知道,选出3名男同学、4名女同学有![]() ·
·![]() 种方法.在将选出的7人进行排列时,由于4名女同学必须排在一起,可先将她们看成一个整体,作为一个元素与3名男同学进行排列,然后将4名女同学进行排列,于是所求的排法种数是:
种方法.在将选出的7人进行排列时,由于4名女同学必须排在一起,可先将她们看成一个整体,作为一个元素与3名男同学进行排列,然后将4名女同学进行排列,于是所求的排法种数是:
![]() 答:共有34560种排法.
答:共有34560种排法.
⑶解法1:在选出的7人中,由于3名男同学必须站在中间,有![]() 种排法,4名女同学分在两侧,有
种排法,4名女同学分在两侧,有![]() 种排法,因此所求的排法种数是:
种排法,因此所求的排法种数是:
![]() 答:共有8640种排法.
答:共有8640种排法.
解法2:从4名男同学中选出3人进行排列,有![]() 种方法;从6名女同学中选出4人进行排列,有
种方法;从6名女同学中选出4人进行排列,有![]() 种方法.根据题意,所求的方法种数是:
种方法.根据题意,所求的方法种数是:![]()
答:共有8640种排法.
2解:(1)证明:取PD中点E,∵E,N分别是PD,PC中点,
∴ ![]()
![]() ∥MN ∵PA=AD ∴AE⊥PD
∥MN ∵PA=AD ∴AE⊥PD
又∵PA⊥平面ABCD ∴PA⊥CD,CD⊥AD (4')
PA∩AD=A ∴CD⊥平面PAD
AE平面PAD ∴AE⊥CD,CD∩PD=D
∴AE⊥平面PCD ∴MN⊥平面PCD (6')
(2)解:连AC交BD于O,则O是AC中点,连ON则ON⊥ABCD (8')
作OF⊥MD,连NF,则NF⊥MD ∴∠NFO是二面角N—DM——C的平面角,
NO=![]() (10')
(10') ![]() ∠NFO=
∠NFO=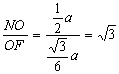
二面角N—MD——C为60° (12’)
3. 解:⑴ 用A表示将合格品鉴定为合格品,B表示将次品鉴定为次品,而用![]() 表示将合格品鉴定为次品,
表示将合格品鉴定为次品,![]() 表示将次品鉴定为合格品.故
表示将次品鉴定为合格品.故![]()
![]() ,
,![]() 3件产品都被鉴定为合格品,说明2件合格品都被正确鉴定,而1件次品被错误地鉴定为合格品了.所以
3件产品都被鉴定为合格品,说明2件合格品都被正确鉴定,而1件次品被错误地鉴定为合格品了.所以
![]()
⑵ 3件产品都被鉴定为次品,说明其中的1件次品被正确鉴定为次品,而2件合格品均被错误地鉴定为次品了,所以
![]() .
.
⑶ 3件产品鉴定为2件合格品1件次品含2种情况:
其一是把2件合格品鉴定为合格品,1件次品鉴定为次品,其二是把其中的1件合格品鉴定为合格品,另一合格品被鉴定为次品,并且其中的1件次品被鉴定为合品.故所求概率为:
![]()
![]()
![]()
![]()
![]() .
.
4.解: (1) 取CC1的中点F, 连接AF, BF, 则AF∥C1D.
∠BAF为异面直线AB与C1D所成的角或其补角.…………(1分)∵△ABC为等腰直角三角形,
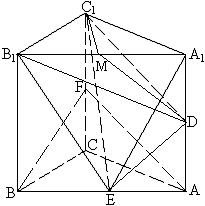 AC=2, ∴AB=2
AC=2, ∴AB=2![]() .又∵CC1=2, ∴AF=BF=
.又∵CC1=2, ∴AF=BF=![]() .
.
∵![]() ∴
∴![]()
∴即异面直线AB与C1D所成的角为![]() ……(4分)
……(4分)
(2) 过C1作C1M⊥A1B 1, 垂足为M, 则M为A1B1的中点,且C1M⊥平面AA1B1B. 连接DM.
∴DM即为C1D在平面AA1B1B上的射影.…………(5分)
要使得A1E⊥C1D, 由三垂线定理知, 只要A1E⊥DM.…………(7分)
∵AA1=2, AB=2![]() , 由计算知, E为AB的中点.…………(8分)
, 由计算知, E为AB的中点.…………(8分)
(3)连接DE, DB1. 在三棱锥![]() 中, 点C1到平面DB1E的距离为
中, 点C1到平面DB1E的距离为![]() ,
,
B1E=![]() , DE=
, DE=![]() , 又B1E⊥DE, ∴△DB1E的面积为
, 又B1E⊥DE, ∴△DB1E的面积为![]()
∴三棱锥C1—DB1E的体积为1.…………(10分)
设点D到平面![]() 的距离为d, 在△
的距离为d, 在△![]() 中, B1C1=2, B1E=C1E=
中, B1C1=2, B1E=C1E=![]() ,
,
∴△B1C1E的面积为![]() .
.
由![]() 得
得![]() , 即点D到平面
, 即点D到平面![]() 的距离为
的距离为![]() .…………(12分)
.…………(12分)
高二下期数学巩固练习(7)
ABCBB DCCDD
11.252 12.![]() 13. 4 14.7 15. 60° 16. 分析: 交换医疗小组的两成员顺序是同一选派方法,故为组合问题
13. 4 14.7 15. 60° 16. 分析: 交换医疗小组的两成员顺序是同一选派方法,故为组合问题![]() 用直接法解:选派5名医生分为2男3女,3男2女,4男1女,5男这四类,故(2)正确; 用间接法解: 不考虑限制条件,选派方法有
用直接法解:选派5名医生分为2男3女,3男2女,4男1女,5男这四类,故(2)正确; 用间接法解: 不考虑限制条件,选派方法有![]() 种,需剔除的有1男4女,5女两类,故(3)正确
种,需剔除的有1男4女,5女两类,故(3)正确![]() 因此结论为: (2)(3)
因此结论为: (2)(3)![]() 点评:本例要特别防止误选(4)
点评:本例要特别防止误选(4)![]()
5.解:3人上火车的方式即基本事件的总数有10×10×10=![]() 个,仅有两人上了同一节车厢另一人上了别的车厢的方式有
个,仅有两人上了同一节车厢另一人上了别的车厢的方式有![]() 种,3人上了同一节车厢的方式有
种,3人上了同一节车厢的方式有![]() 种,则至少有2位同学上了同一车厢的概率为
种,则至少有2位同学上了同一车厢的概率为![]() .选D.
.选D.
高二下期数学巩固练习(8)
1.解:设取![]() 个红球,
个红球,![]() 个白球,于是:
个白球,于是:
![]() ,其中
,其中![]() ,
, ![]()
因此所求的取法种数是:![]() =186(种)
=186(种)
2.解(Ⅰ)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.
取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(Ⅱ)由CD⊥平面ABM,则平面ABM⊥平面BCD,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,![]() . 在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=
. 在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=![]() . 在Rt△BCM中,BC=
. 在Rt△BCM中,BC=![]() ,CM=1,
,CM=1,
![]() .
.![]()
3.
解:x=25或![]()
提示:2n-1=32,中间项![]() =2500,
=2500,
即![]()
![]() log5x(log5x-1)=1
log5x(log5x-1)=1
4.(Ⅰ)在△ABC中,AB=![]() ,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
又BC⊥A1O,故BC⊥侧面AC1,AB与侧面AC1所成角就是∠BAC=45°.
(Ⅱ)由(Ⅰ)知四边形B1BCC1为矩形,![]() 中点,
中点,
![]() 于E,连结A1E,则AB⊥A1E. 在Rt△AOE
于E,连结A1E,则AB⊥A1E. 在Rt△AOE
中,![]() ,在Rt△A1EO中,
,在Rt△A1EO中,![]()
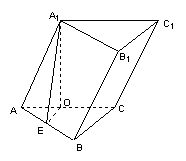
![]() .
.
欢迎访问 http://www.k12zy.com