高二下期期末立体几何专项练习
一、选择题：
1．已知相交直线
都在平面
内，且都不在平面
内，若
：中至少有一条与相交；
：与相交，则是的
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．不充分也不必要条件
2．下面几个命题：
①“直线
直线
”的充要条件是“
平行于所在的平面”；
②“直线
平面内所在直线”的充要条件是“”
③“直线、为异面直线”的充分不必要条件是“直线、不相交”；
④“平面
平面”的必要不充分条件是“内存在不共线的三点到的距离相等”。
其中正确的命题是
A．①② B．②③ C．③④ D．②④
3若
是两条异面直线，则总存在一个确定的平面，满足
A．
，
B．
， C．
，
D．，
4．在四棱锥
中，为了推出
，需从下列条件：①
面
；
②
；③
面
；④
中选出部分条件，这些条件可能是
A．②③ B．①④ C．②④ D．③④
5．设、是两条不同直线，、是两个不同平面，则下列命题
①
②
③
④
其中正确的命题的个数是
A．0个 B．1个 C．2个 D．3个
6．设
是直线，、是平面，给出下列三个条件：①
；②
；③
以其中两个作为题设，另一个作为结论，则可构成三个命题，这三个命题中正确的个数为
A．3个 B．2个 C．1个 D．0个
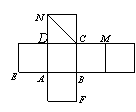7．如图是一个正方体的平面展开图，在这个正方体中
①
②
与
成
角
③与为异面直线 ④
以上四个命题中，正确的序号是
A．①②③ B．②④ C．③④ D．②③④
8．在正方体
中，各面对角线所在的
条直线中与对角线所在直线异面且垂直的有
A．2条 B．4条 C．6条 D．8条
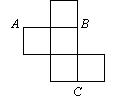9．如图，一个无盖的正方体盒子的表面展开图，
、
、
为其上
的三点，则在正方体盒子中
A．
B．
C．
D．
10．在侧棱垂直于底面的三棱柱
中，
，
、
分别为
、
的中点，点
在线段
上，则
与平面
的位置关系为
A．垂直
B．平行 C．相交但不垂直 D．由点的位置而定
11．已知是⊙
的直径，
面⊙，是⊙上一点（不包括
两点），则二面角
的平面角是
A．锐角 B．直角 C．钝角 D．不能确定
12．正方体的棱长为，
在上滑动，且
，点
在
上滑动，则四面体
的体积
A．与
、
位置有关 B．与点位置有关 C．与
位置都有关 D．定值
13．一个水平放置的图形的斜二测直观图是底角为，腰和上底均为 
的等腰梯形，则原图形的面积为
A．
B．
C．
D．
14．过棱长为
的正方体同一顶点的三条棱的中点作一截面，将正方体截下一角，则剩余部分的体积为
A．
B．
C．
D．
15．球面上有四个点
，若
两两互相垂直，且
，那么这个球队的球面面积为
A．
B．
C．
D．
16．在棱长为1的正方体中，是底面
的中心，则到平面
的距离为
A．
B．
C．
D．
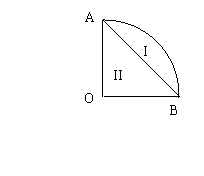17．如图，扇形的中心角为
，弦将扇形分成两部分，这两部分各以
为轴旋转一周，所得的旋转体体积
的比为
A．
B．
C．
D．
18．两个完全相同的长方体的长、宽、高分别为
、
、
，把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度为
A．
B．
C．
D．
19．已知底面为正三角形的三棱锥
的三条侧棱两两成
角，侧棱长为
，
、为
与
的点，则△
的周长最小值为
A．
B．
C．
D．
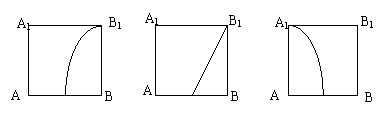
20．正方体中，在侧面
内有一动点，它到直线与到直线
的距离相等，则点的轨迹是下图中的
 | |||
 | |||
A． B． C． D．
二、填空题：
21．设平面、和直线、，给出下列命题：
① 若
，
，则
② 若，
，
，则
③ 若，，则 ④ 若，
，
，则
⑤ 若，
，则
其中正确命题的序号是_____________.（将所有正确结论的序号都写上）
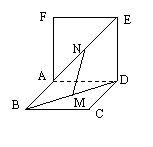
22．如图，两个正方形和
所在平面互相垂直，设、分别是
和
的中点，那么① 
；② 
面
；③ 
；④ 
、
异面
其中正确结论的序号是_____________.
23．正方体中，为
的中点，则
与面
的位置关系为_____________.
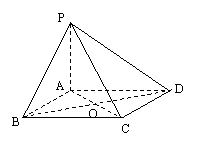
24．如图，四棱锥
中，为正方形，底面，那么在该图中，互相垂直的平面有___________对.
25．在正方体中，为底面的中心，、、
、
分别为棱
、
、
、的中点，请写出一个与
垂直的正方体的截面_____________.（截面以给定的字母表示，不必写出所有情况）
26．设
、
、
表示空间的不同直线或平面，且直线不在平面内，给出下列五个命题：
① 为直线，、为平面；② 、、为平面；③ 、为直线，为平面；④、为平面，为直线；⑤ 、、为直线。则其中能保证“若
且
，则
”为真命题的是_____________.（填所有正确条件的代号）
27．将棱长为1的正方体木块加工成一个体积最大的球，则被去掉的木料的总体积为____________.
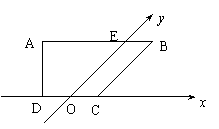
28．如图，是一平面图形的水平放置的斜二测直观图，在直观图中，是一直角梯形，
，
，且
轴。若
，
，则这个平面图形的实际面积是____________.
29．棱长为4的正方体的内切球的体积为____________，若点为上的动点，则
的最小值为____________.
30．一个圆柱形容器的内半径为
，内装深为
的水，将一个钢球完全浸入水中，这时容器中水的高度升至
，那么钢球的半径为____________.
三、解答题：
31．在棱长为的正方体中。
（1）求证：
面
；
（2）求证：面
面；
（3）求证：
面；
（4）求证：面
面
；
（5）求三棱锥
的体积。
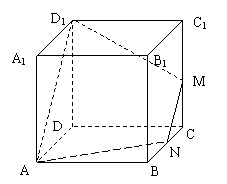32．已知正方体中，点、分别为、的中点。
（1）求证：、、、
四点共面；
（2）证明多面体
是棱台。
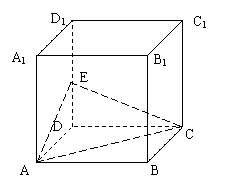
33．如图，在长方体中，
，
，点是棱
的中点。
（1）求截面
的面积；
（2）求三棱锥
的体积
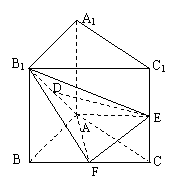34．已知侧棱垂直于底面的三棱柱中，底面
为等腰直角三角形，
，且
，、、分别为
、
、的中点。
（1）求证：
面；
（2）求证：
面
。
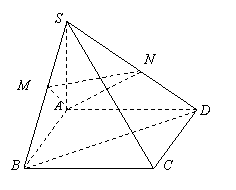
35．如图，在四棱锥中，底面为正方形，
底面，
，、分别为
、
的中点。
（1）求证：
面
；
（2）求证：
面。
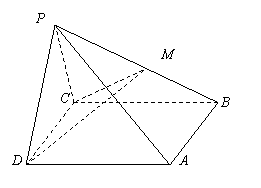36．如图，四棱锥中，侧面
为正三角形，且与底面垂直，已知底面是面积为
的菱形，
，为的中点，求证：
（1）
；
（2）面
面
。
立体几何专项训练简答
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | D | B | D | B | C | B | C | B | B |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| B | D | D | D | C | B | A | C | B | A |
二、填空题：
21．④；
22． ①②③；
23．
面； 24．
；
25．
（或
或
）； 26．①③④； 27．
； 28．
；
29．
；
30．
；
三、解答题：
欢迎访问 http://www.k12zy.com