云外08高高二下期数学阶段测试七
(期末模拟试题)
一、选择题(共50分)
1.从5个一中学生、4个二中学生、3个三中学生中各选一人的选法有
A.12种 B.24种 C.48种 D.60种
2.下列等式中不正确的是
A.C![]() B.C
B.C![]()
C.C![]() D.C
D.C![]()
3.甲、乙两人同时报考南京大学,甲被录取的概率为0.6,乙被录取的概率为0.7,两人是否录取互不影响,则其中至少一人被录取的概率为:
A.0.12 B.0.42 C.0.46 D.0.88
4.![]() 、
、![]() 是两个不重合的平面,
是两个不重合的平面,![]() 和
和![]() 是不重合的两条直线,则
是不重合的两条直线,则![]() 的一个充分条件是
的一个充分条件是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. 要完成下列2项调查:①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标;②从邵东一中排球队12名队员中选出3人调查学习负担情况.应采用的抽样方法是
A.①用随机抽样法,②用系统抽样法
B.①用分层抽样法,②用随机抽样法
C.①用系统抽样法,②用分层抽样法
D.①、②都用分层抽样法
6.在棱长为a的正方体ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,M是AA
中,M是AA![]() 的中点,则点A
的中点,则点A![]() 到平面MBD的距离是
到平面MBD的距离是
A.![]() a B.
a B.![]() a C.
a C.![]() a D.
a D.![]() a
a
7.若圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)关于直线y=x+1对称,则下列结论成立的是
A.D+E=1 B.D-E=1 C.D+E=2 D.D-E=2
8.已知三角形ABC的顶点是![]() ,若
,若![]() ,则顶点
,则顶点![]() 的轨迹方程是
的轨迹方程是
A.![]() .
B.
.
B.![]()
C.![]() D.
D.![]()
9.点M是椭圆![]() 上的一个动点,F1,F2是椭圆的两个焦点,则
上的一个动点,F1,F2是椭圆的两个焦点,则![]() 的最小值是( )
的最小值是( )
A.1 B.3
C.4
D.![]()
10.设在4次独立重复试验中,事件A出现的概率相同。若已知事件A至少发生一次的概率等于![]() ,则事件A在一次试验中出现的概率是
,则事件A在一次试验中出现的概率是
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
二、填空题(共24分)
11.已知(1-3x)6=a0+a1x+a2x2+…+a6x6.
则a1+a2+…+a6=_____________________ .
12.已知椭圆![]() =1的离心率为
=1的离心率为![]() ,则实数m的值为
,则实数m的值为
13.已知A(x1,y1),B(x2,y2)是抛物线y2=2x的一条焦点弦的两个端点。则x1x2+y1y2=____________.
14.已知![]() 的展开式中,
的展开式中,![]() 的系数为
的系数为![]() ,则常数
,则常数![]() 的值为____________.
的值为____________.
15.摇奖器摇出的一组中奖号码为8,2,5,3,7,1。对奖票上的六个数字是从0,1,2,……,9这十个数字中任意选出六个不同数字组成的。如果对奖票上的六个数字中至少有五个与摇奖器摇出的号码相同(不计顺序)就可以得奖,则中奖的概率为 .
16. 三棱锥P-ABC的四个顶点在同一球面上, 若PA⊥底面ABC,底面ABC是直角三角形,PA=2,AC=BC=1,则此球的表面积为 .
班级 学号 姓名 得分
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
11. 12.
13. 14.
15. 16.
三、解答题(共76分)
17.![]()
![]() 若
若![]() ,求a的取值范围.
,求a的取值范围.
18. 求由约束条件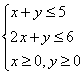 确定的平面区域的面积
确定的平面区域的面积![]() 和周长
和周长![]() .(12分)
.(12分)
19.(12分)已知圆C1:(x+5)2+y2=49,圆C2:(x-5)2+y2=1,动圆M与圆C1和圆C2都外切。求动圆的圆心M的轨是方程。
20.(12分)高三(1)班、高三(2)每班已选出3名学生组成代表队,进行乒乓球对抗赛,比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,不得参加两盘单打比赛;③先胜两盘的队获胜,比赛结束.已知每盘比赛双方胜出的概率均为![]()
(Ⅰ)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率是多少?
(Ⅲ)高三(1)班代表队至少胜一盘的概率为多少?
21.(14分)如图,四棱锥S-ABCD的底面ABCD是正方形,
SA⊥底面ABCD,E是SC上的一点,
(1)求证:平面EBD⊥平面SAC;
(2)若SA=4,AB=2,求点A到平面SBD的距离;
 (3)当
(3)当![]() 的值为多少时,二面角B-SC-D的大小为
的值为多少时,二面角B-SC-D的大小为![]() ?
?
22.(14分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上,其右焦点到直线x-y+2![]() =0的距离为3。(1)求椭圆的方程;(2)椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N。当AM=AN时,求m取值范围。
=0的距离为3。(1)求椭圆的方程;(2)椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N。当AM=AN时,求m取值范围。
云外08高高二下期数学阶段测试七
数学参考答案
一、选择题
1.D 2.D 3.D 4.C 5.B 6.A 7.D 8.D 9.B 10.A
二、填空题
11. 63 12.8或2 13. ![]() 14.4 15.
14.4 15.
![]() 16.
16. ![]()
三、解答题
17.[解析]:由![]() 可得
可得
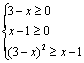
![]()
又由![]() 可得
可得![]() ,
,
即![]() ,
,
因为![]() ,画数轴如下:
,画数轴如下:

由图可知,![]() , 所以,得a≥1
, 所以,得a≥1
18.(12分)
[解析]:由约束条件作出其所确定的平面区域(阴影部分),其四个顶点为O(0,0),B(3,0),A(0,5),P(1,4).过P点作y轴的垂线,垂足为C.
则AC=5-4=1,PC=1-0=1,OC=4,OB=3,AP=![]() ,
,
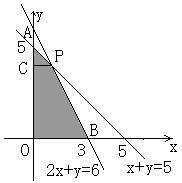 PB=
PB=![]()
得![]() =
=![]() ,
,
![]()
所以![]() =
=![]() +
+![]() =
=![]() ,
,
![]() =OA+AP+PB+OB=8+
=OA+AP+PB+OB=8+![]() +
+![]()
19.解设动圆M的半径为r,并设M(x,y)圆C1:r1=7,C1(-5,0),圆C2:r2=1,C2(5,0)
∵![]()
![]() ∴
∴![]() ,M的轨迹是以C1,C2为焦点,实轴长为6的双曲线右支a=3,c=5,所求方程
,M的轨迹是以C1,C2为焦点,实轴长为6的双曲线右支a=3,c=5,所求方程![]() (x≥3)
(x≥3)
20.(Ⅰ)参加单打的队员有![]() 种方法.
种方法.
参加双打的队员有![]() 种方法.
种方法.
所以,高三(1)班出场阵容共有![]()
(Ⅱ)高三(1)班代表队连胜两盘,可分为第一盘、第二盘胜或第一盘负,其余两盘胜.
所以,连胜两盘的概率为![]() )
)
(Ⅲ)高三(1)班至少胜盘,可分为:
(1)胜一盘,此时的概率为
![]()
(2)胜两盘,此时的概率为
![]()
所以,高三(1)班至少胜一盘的概率为![]()
或:高三(1)班代表队至少胜一盘的对立事件为输掉前两盘
所以,所求概率为![]()
21.解:1)略;(2)![]() ;(3)1
;(3)1
22.解(1)由已知设椭圆方程为![]() =1(a>b>0),其中b=1,设右焦点为(c,0),则
=1(a>b>0),其中b=1,设右焦点为(c,0),则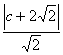 =3,解得c=
=3,解得c=![]() ,所以a=
,所以a=![]() ,所以椭圆方程为
,所以椭圆方程为![]() +y2=1
+y2=1
![]() y=kx+m
y=kx+m
(2)设P为MN的中点,解方程组
x2+3y2-3=0
得(3k2+1)x2+6mkx+3(m2-1)=0
因为相交两点,所以△=-12m2+36k2+12>0,得m2<3k2+1
xM+xN=![]() xP=
xP=![]() 所以yP=kxP+m=
所以yP=kxP+m=![]()
所以kAP=![]() 由MN⊥AP得
由MN⊥AP得![]() =-
=-![]()
即得2m=3k2+1代入m2<3k2+1得0<m<2,
又由2m=3k2+1的k2=![]() 得m>
得m>![]()
综上![]() <m<2为所求。
<m<2为所求。
欢迎访问 http://www.k12zy.com