高二下期阶段测试五

08高高二下期数学阶段测试五

（重庆市重点中学高2007级高二下数学期末模拟考试试题）

一、选择题（共50分）

1．C⁵₂₀+C⁴₂₀+C⁴₂₁=（　　）

A．C⁵₂₁　　　B．C⁴₂₂　　　C．C⁵₂₂　　　D．C⁴₂₁

2．α表示一个平面，l表示一条直线，则α内至少有一条直线与直线l （　　）

A．平行　　 B．相交　　　　C．异面　　　 D．垂直

3．某气象站天气预报的准确率为80%，则5次预报中至少有4次准确的概率（结果保留两位有效数字）是（　　）

A．0.23　　 B．0.41　　　C．0.74　　　D．0.67

4．一个正四棱锥的底面面积为Q，则它的中截面的边长是（　　）

A．　 B．　　 C．　　 D．

5．10名学生计划“五一”这天去郊游，本着自愿的原则，规定任何人可以“去”或“不去”，则这10名学生“五一”这天去郊游的情况共有（　  ）

A．C种　 B．A种　　C．10²种　　　D．2¹⁰种

6．棱长为a的正方体ABCD-A₁B₁C₁D₁中，AB的中点为M，DD₁的中点为N，则异面直线A₁M与C₁N所成角的大小为（　　）

A．30°　　B．45°　　  C．60°　　 D．90°

7．由0，1，2，3组成比300大的无重复数字的自然数一共有（　　）

A．6　　　　B．18　　　　　 C．24　　　　 D．28

8．正二十面体的各面都是正三角形，且每一个顶点为其一端都有五条棱，则其顶点数和棱数的值分别是（　　）

A．V=3、E=12　　　　　　　 B．V=12、E=30　

C．V=6、E=12　　　　　　　 D．V=12、E=6

9．某地区的年降水量（单位：mm）在[100，150]、[150，200]、[200，250]范围内的概率分别为0.12、0.25、0.16，则年降水量在[100，200]范围内的概率为（　　）

A．0.53　　B．0.25　　 C． 0.37　　 D．0.28

10．长方体的一个顶点上三条棱的长分别是3，4，5，且它的八个顶点都在同一球面上，这个球的表面积是（　　）

A．20π　B．25π　　 C．50π　　D．200π

二、填空题（共24分）

11．已知（1＋x）＋（1＋x）²＋…＋（1＋x）ⁿ＝a₀＋a₁x＋…＋a_nxⁿ，若a₁＋a₂＋a₃＋…＋a_n－1＝29－n，则自然数n的值应为　　　　   .

12．二面角a—l—β为60°，P∈α，P到平面β的距离为，则P在平面β上的射影O到平面α的距离为　　　　   .

13．设地球半径为R，在南纬30°圈上有A、B两点，这两点的经度差为π，则A、B两点的球面距离为　　　　　　 .

14．5名同学安排在周一至周五值日，每人一天，若甲同学不能排在星期一，乙同学不能排在星期五，则所有不同的排法种数为　　　　　　  .（用数字作答）

15．2³³除以9的余数是　　　　　　  　.

16．已知：m，l是直线，α、β是平面，给出下列5个命题：

①若l垂直于α内两条相交直线，则l⊥α.　②若l∥α，则l平行于α内的所有直线.　③若mα，lβ，且l⊥m，则α⊥β.　④若lβ，且l⊥α，则α⊥β.　⑤若m α，lβ，且α∥β，则m∥l.

其中正确的命题序号是　　　　 .（写出所有真命题的序号）

班级　　　学号　　　　姓名　 　　　　　得分　　　　　

1	2	3	4	5	6	7	8	9	10

11．　　　　　　　　　　　　　12．　　　　　　　　　　　

13．　　　　　　　　　　　　　14．　　　　　　　　　　 

15．　　　　　　　　　　  　　16．　　　　　　　　　　 

三、解答题（共76分）

 17．（13分）求证：如果一个平面与另一个平面的垂线平行，那么这两个平面互相垂直.

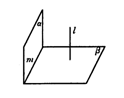已知：

求证：

证明：

18．（本小题满分13分）已知（x）ⁿ的展开式的前三项系数和为129，求展开式中含x的项（即x的一次方项）.

19．（本小题满分13分）已知：甲袋中有3个黑球，2个白球；乙袋中有4个黑球，5个白球.

（Ⅰ）从甲袋中任意取出两个球，求取得一黑一白的概率；

（Ⅱ）从甲、乙两袋中分别取出一个球，求取得一黑一白的概率.

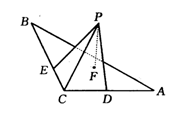20、（本小题满分13分）如图，在△ABC中，∠C是直角，平面ABC外一点P，PC=24cm点P到直线AC、BC的距离PD和PE都等于6cm.

（Ⅰ）求点P到平面ABC的距离PF；

（Ⅱ）求PC与平面ABC所成的角.

21、（本小题满分12分）甲、乙、丙3人各进行1次射击，若3人击中目标的概率分别是，，.求3人中至少有1人击中目标的概率.

22、（本小题满分12分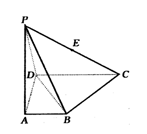）如图：在四棱锥P-ABCD中，PA⊥平面ABCD，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点.

（Ⅰ）求证：平面PDC⊥平面PAD；

（Ⅱ）求证：EB∥平面PAD；

（Ⅲ）当PA=AD=DC时，求二面角E—BD—C的正切值.

参考答案

一、选择题：CDCAD　　 DCBCC　

二、填空题：（11）4　（12）　　（13）πR　　（14）78　　（15）8　　（16）①④

三、解答题：

（17）已知：α∩β=m，l⊥β，l∥α.

求证：α⊥β.（2分）

证明：在α内任取一点P，

∵l∥α，　∴Pl.设l和点P确定的平面为γ.（5分）

设γ∩α=l′，则l∥l′.（8分）

l⊥β 　l′⊥β

α⊥β.（13分）

l∥l′　　 l′α

（18）解：依题意知：1+C_n¹·2+C_n²·2²=129，　　∴n=8.（3分）

（x+）⁸的展开式的通项是

T_r+1=C₈^r（）^r·（x）^8-r=C₈^r·2^r·x^-（8分）

根据题意，得-=1，r=6.　　　　　　　（10分）

因此，含x的项是T₆₊₁=C₈⁶（）⁶·（x）²=1792x.（13分）

（19）解：（Ⅰ）从甲袋中任取两球的总数为C₅²=10，取得一黑一白的总数为C₃¹·C₂¹=6，

所求的概率为P₁==.

答：从甲袋中任意取出两球，得到一黑一白的概率为.（6分）

（Ⅱ）甲袋中任意取出黑球的概率为，取出白球的概率为；乙袋中取出黑球的概率为，取出白球的概率为.因此所求概率P₂=·+·=.　　　　　　　（12分）

答：从甲、乙两袋中分别取出一个球，得到一黑一白的概率为.（13分）

（20）解：连EF、DF、CF，则EF⊥BC，DF⊥AC.又PE=PD=6，PF垂直于平面ABC，

∴EF=DF.　　∴∠BCF=∠ACF=45°.（4分）

（Ⅰ）在Rt△PEC中，得EC=6（cm），在Rt△PEF中，得PF=12（cm）.（8分）

（Ⅱ）∵PF垂直于平面ABC，

∴∠PCF即为PC与平面ABC所成的角.

在Rt△PCF中，sin∠PCF==，∠PCF=30°，

故PC与平面ABC所成的角为30°.（13分）

（21）解：分别记甲、乙、丙3人击中目标为事件A，B，C.由题意，3人是否击中目标相互之间没有影响.（3分）

根据相互独立事件的概率乘法公式，3人都未击中目标的概率是

P（··）=P（）·P（）·P（）=[1-P（）]·[1-P（）]·[1-P（）].

=（1-）·（1-）·（1-）=.（9分）

故3人中至少有1人击中目标的概率为

1-P（··）=1-=.（11分）

答：3人中至少有1人击中目标的概率是.（12分）

（22）（Ⅰ）证明：PA⊥平面ABCD

　　　　　　　　　　　　　　　　  CD⊥平面PAD

CD⊥AD　　　　　　　　　　

　　　　　　 CD平面PCD

平面PCD⊥平面PAD.　　　 （4分）

（Ⅱ）证明：设F是PD的中点，则EF平行且相等CD

　EF平行且相等AB AB平行且相等CD

四边形EFAB是平行四边形EB∥AF

AF平面PAD　　EB∥平面PAD.（8）

BE平面PAD

（Ⅲ）解：设O为AC的中点，则EO平行且相等PA.

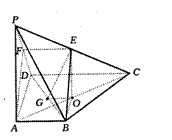∵PA⊥平面ABCD，

∴EO⊥平面ABCD.作OG⊥BD于G，连结EG，

则EG⊥BD.

∴∠EGO为二面角E-BD-C的平面角.（11分）

设PA=AD=DC=2a，则AB=a，AO=a，

∠OAB=45°.

由余弦定理求得OB=a，而OB²+AB²=AO²，

 ∴OB⊥AB.∴Rt△OGB∽Rt△BAD，

.　 ∴OG=a.OE=PA=a.

∴tan∠EGO==,

即二面角E-BD-C的正切值为.（12分）

欢迎访问 http://www.k12zy.com