08高高二下期数学阶段测试四
一、选择题(共50分)
1.![]()
A.20 B.17 C.11 D.10
2.![]() 的展开式的第六项的系数是
的展开式的第六项的系数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.直线a、b、c两两平行,但不共面,经过其中两条直线的平面共有:
A.0个 B.2个 C.3个 D.4个
4.在下列关于直线![]() 与平面
与平面![]() 的命题中,真命题是
的命题中,真命题是
A.若![]() ,
,![]() ,则
,则![]() .
.
B.若![]() ,
,![]() ,则
,则![]() .
.
C.若![]() ,
,![]() ,则
,则![]()
D.若![]() ,
,![]() ,则
,则![]() .
.
5.有送信、抬水和守护教室三项任务,送信和守教室各需1人承担,抬水需要2人承担,现从10人中选派4人承担这三项任务,不同的选派方法种数为:
A.1260种 B.2025种 C.2520种 D.5040种
6.四个不同的小球放入编号为1、2、3、4的四个盒子中,则恰有一个空盒的放法种数为:
A.36 B.72 C.64 D.144
7.若![]() 的展开式的系数和等于
的展开式的系数和等于![]() 的展开式的二项式系数之和,则
的展开式的二项式系数之和,则![]() 的值是
的值是
A.15 B.10 C.8 D.5
8.用1,2,3,4,5组成无重复数字的五位数,其中大于20000且不是5的倍数的五位数的个数是
A.96 B.78 C.72 D.36
9.如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]()
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() 为
为![]() 上任意两点,且
上任意两点,且![]() 长为定值. 则下面的四个值中,不为定值的是
长为定值. 则下面的四个值中,不为定值的是
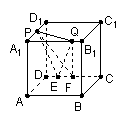 A.点
A.点![]() 到平面
到平面![]() 的距离
的距离
B.直线![]() 与平面
与平面![]() 所成的角
所成的角
C. 二面角![]() 的大小
的大小
D. 三棱锥![]() 的体积
的体积
10.点![]() 为四面体
为四面体![]() 的侧面
的侧面![]() 内的一点,若侧面
内的一点,若侧面![]() 内的动点
内的动点![]() 到底面
到底面![]() 的距离与到点
的距离与到点![]() 的距离相等,则动点
的距离相等,则动点![]() 在侧面
在侧面![]() 内的轨迹是
内的轨迹是
A.椭圆的一部分 B.椭圆或双曲线的一部分
C. 双曲线或抛物线的一部分 D.抛物线或椭圆的一部分
二、填空题(共24分)
11.![]() =
=
12.五个旅客入住3个不同的房间,每个房间至少入住1人,则不同的入住方法有 .
13.在正三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点,且
的中点,且![]() ,若侧棱
,若侧棱![]() ,则正三棱锥
,则正三棱锥![]() 外接球的表面积是 .
外接球的表面积是 .
14.以等腰直角三角形斜边上的高为棱把它折成直二面角,则折成后两直角边的夹角为 .
15.(x+y)5的展开式第2项是240,第3项是720,则x= ,y=
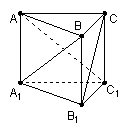
16.如图,直三棱柱![]() 中,给出下列三个条件:
中,给出下列三个条件:
① ![]() ; ②
; ② ![]() ;③
;③ ![]() ;
;
利用①②③中的任意两个作为条件,另外一个作为结论,
可以构造出三个命题,其中正确命题的个数是 .
 |
班级 学号 姓名 得分
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
11. 12.
13. 14.
15. 16.
三、解答题(共76分)
17.(本小题满分13分) 用1,2,3,4,5这五个数字中的三个组成没有重复数字的三位数.
(I)不同的三位数有多少个?
(II)若所组成的三位数中既含有奇数数字,又含有偶数数字,则不同的三位数有多少个?
18 (本小题满分13分)已知![]() 的展开式中第五项的系数与第三项的系数之比为
的展开式中第五项的系数与第三项的系数之比为![]() .
.
(I)求![]() 的值;
的值;
(II)求展开式中含![]() 的项.
的项.
19.(本小题满分13分)在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() .
.
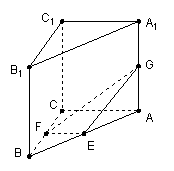 (I)求
(I)求![]() 的长;
的长;
(II)求直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的大小.
的大小.
20(本小题满分13分) 如图,三棱柱![]() 的底面是边长为2的等边三角形,侧面
的底面是边长为2的等边三角形,侧面![]() 是
是![]() 的菱形,且平面
的菱形,且平面![]() 平面
平面![]() ,点
,点![]() 是
是![]() 上的动点.
上的动点.
(I)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() 面
面![]() ;
;
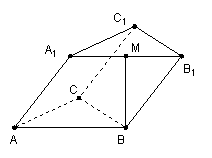 (II)当二面角
(II)当二面角![]() 的平面角最小时, 求三棱锥
的平面角最小时, 求三棱锥![]() 的体积.
的体积.
21.(本小题满分12分)已知![]() 的展开式中含
的展开式中含![]() 项的系数相等,求实数
项的系数相等,求实数![]() 的取值范围.
的取值范围.
22.(本小题满分12分)
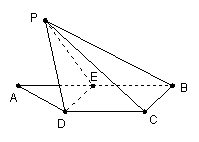
如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 折到点
折到点![]() 的位置,且二面角
的位置,且二面角![]() 的大小为
的大小为![]() .
.
(I)求证:![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 的大小.
的大小.
DDCB? ?DDBD ? 150 ![]()
![]()
? 3
三、解答题:17. (I)![]() ; (II)
; (II) ![]() 或者
或者![]() .
.
18 (I)![]() ,由
,由![]() ,得
,得![]() ;(II)令
;(II)令![]() ,得
,得![]() ,故
,故![]() ;
;
19(I)以![]() 为原点建系,易得
为原点建系,易得![]() 是
是![]() 的中点;(II)平面
的中点;(II)平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]() .
.
20.解:(1)∵ABB1A1是菱形,∠A1AB=60°,且M为A1B1的中点,
∴BM⊥A1B1, …………2分
又A1B1∥AB,∴MB⊥AB.平面ABB1A1⊥平面ABC,
∴MB⊥平面ABC.
又AC![]() 平面ABC,∴BM⊥AC. …………6分
平面ABC,∴BM⊥AC. …………6分
(2)作CN⊥AB于N,由于△ABC为正三角形,知N为AB为中点,又平面ABB1A1⊥平面ABC,∵CN⊥平面A1ABB1,作NE⊥MB于E点,连CE,由三垂线定理可知CE⊥BM, ∴∠NEC为二面角A1—BM—C的平面角.………9分
由题意可知CN=![]() ,在Rt△CNE中,
,在Rt△CNE中,![]() 要∠NEC最小,只要NE取最大值.
要∠NEC最小,只要NE取最大值.
又∵△A1B1B为正三角形,∴当M为A1B1中点时,MB⊥平面ABC,即E与B重合.
此时NE取最大值且最大值为1,∴![]() .
.
∴∠NEC的最小值为60°,……10分
此时![]() .……14分
.……14分
21.解:设![]() 的通项公式为
的通项公式为![]() ,则
,则![]() .令
.令![]() ,得
,得![]() 故此展开式中
故此展开式中![]() 项的系数为
项的系数为![]() 由题意知:
由题意知:![]()
![]()
22(I) ![]() 为平行四边形,连结AC交DE于O,可证
为平行四边形,连结AC交DE于O,可证![]() 且
且![]() ,
,![]()
![]() .
.
(II)![]() ,
,![]() ,
,![]()
![]() ,作
,作![]() ,则
,则![]() ,又
,又![]() ,
,![]() 为所求的距离,
为所求的距离,![]() ;
;
(III)![]() ,连
,连![]() ,可知
,可知![]() 为所求二面角,
为所求二面角,![]() ,
,![]() ,求得
,求得
![]() .
.
欢迎访问 http://www.k12zy.com