2005 -2006学年度第一学期期中考试答案
高 一 数 学
| 题号 | 一 | 二 | 三 | 四 |
| 得分 |
|
|
|
|
| 得分 |
| ||
|
|
|
1、设全集
，集合
，
,则
等于
（ A ）
A、{1，2} B、{3，4} C、{1，2，5，} D、{1，2，3，4，5}
2、若命题
，对复合命题的下述判断：① p或q为真；
② p或q为假 ③ P且q为真；④ p且q为假 ⑤非p为假。 （ D ）
A、①④⑤ B、①③⑤ C、②④ D、①④
3、在（1）
；（2）
与
；（3）
与
；
（4）
与
；（5）
与
这五组中函数图象相同的有（B ）组。
A、0 B、1 C、2 D、3
4、已知
，则满足条件的集合A的个数是（B ）
A、3个 B、4个 C、6个 D、8个
5、函数
的定义域是 （ D ）
A、
B、
C、
D、
6、设函数
，则
的值等于 （ A ）
A、
B、
C、
D、
7、若函数
的图象经过点(0、-1)，则其反函数的图象必经过
（ C
）
A．（0，-1） B.（0，1） C.（-1，0） D.（1，0）
8、函数y=x2(x≤0)的反函数为 （C ）
A． 
B.
C.
D.
9.若不等式ax2+2ax-4<2x2+4x对任意实数x均成立，则实数a的取值范围为：（B ）
A.（-2、2） B.（-2、2］ Ｃ.（-∞，-２）∪［２，+∞） Ｄ.（-∞，-２）
10.已知P={x 0<x<4}, Q={y0<y<2}下列不表示从Ｐ到Ｑ的映射是（C ）
Ａ．
Ｂ．
Ｃ.
Ｄ.
| 得分 |
| ||
|
|
|
11.设Ａ＝｛x1<x<2｝,B={xx<a}且Ａ∪Ｂ＝Ｂ则实数a的范围为a∈[2,+∞] (用区间表示)
12.已知U=R,集合
,
，则Cu(A∪B)={x-4≤x≤-2}([-4,-2])
13. 设(x,y)在映射f下的像为(
),则在f下(-4,2)的像为(-1,-3),(-5,2)的原像为(-3,-7)
14.已知函数f(x)=x2+2(a-2)x+5在区间[4,+∞)上是增函数,则实数a的取值范围为_a≥-2.
15.命题:“若x+y=0，则x,y全为0”的逆否命题为_若x,y不全为0，则x+y≠0_.其真假性为_真__(真,假)
| 得分 |
| ||
|
|
|
16. (11分)已知两个命题P: 3x-4>2. q: 
试问:￢P是￢q的什么条件?
解： ∵P：3x-4>2 q: 
∴¬p: 3x-4≤2 ¬q
∴¬p: 2/3≤x≤2 ¬q: -1<x<2
∴¬p ¬q; ¬q ¬ p
∴¬p是¬q的不充分不必要条件。
17．(8分)<1>求函数
的定义域.
解： -x2+5x+6≥0
∵ x+1-3≠0
x-1≠0
-1≤x≤ 6
∴ x≠2 且x≠-4
x≠1
∴ -1<x<6 且 x≠2 且 x≠1
<2>已知函数f(x)=x2-2x-3,在下列条件下试求出f(x)的值域.
①1≤x<3 ②0≤x≤4
解：① -4≤y≤0 ② -4≤y≤5
18.(10分)讨论函数
在区间（-∞，2）上的单调性
。
解：设x1<x2∈(-∞,2)
∴ 
=
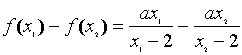
又∵x1<x2<2 ∴ x2-x1>0 x1-2<0 x2-2<0
∴
∴ 当a>0时，f(x1)-f(x2)>0
∴f(x)在（-∞，2）上单调递减，
当a<0时，在（-∞，2）上单调递增。
19.（8分）已知f(x)是定义在[-3，3]上的增函数，且满足f(t-1)<f(1-t2),试求t的取值范围。
.解：∵f(x)的定义域为[-3，3]上的增函数
f(t-1)<f(1-t2)
t-1<1-t2 t2+t-2
<0
∴ -3≤t-1≤3 ∴ -2≤t≤4
-3≤1-t2≤3 -2 ≤ t2 ≤4
-2<t<1
∴ -2≤t≤4 ∴ -2<t<1
-2≤t≤2
20（11分）西安市的出租车按如下方法收费：起步价6元，可行3公里（不含3公里）；3————10公里（不含10公里）按1.3元/公里 计价 (不足1公里按1公里计算);10公里以后都按2元/公里(不足1公里按1公里计算). 若张老师有事到外地出差,他从家门口搭乘出租车到火车站,路程大约为5公里.试写出张老师在搭乘出租车的过程中总费用y与公里数x之间的函数关系式.并画出图像.
6
0<x<3
解：y= 7.3 3≤x<4
8.6
 |
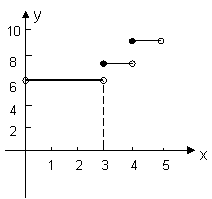4≤x<5