高中一年级比赛考试数学试题
(注意: 试卷满分150分，答题时间为120分钟.只交答卷.)
一、选择题（每小题5分，共50分）：
（1）下列说法中，正确的是 （ ）
A．第二象限的角是钝角． B．第三象限的角必大于第二象限的角
C．
是第二象限角 D．
是终边相同的角
（2）、已知不等式
成立的充分不必要条件是
，则实数
的取值范围
A、
B、
C、
D、
（3）为了得到函数
的图象，只需把函数
的图象上所有的点
（ ）
A．向左平移
个单位长度，再把所得各点的横坐标缩短到原来的
倍（纵坐标不变）
B．向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）
C．向左平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）
D．向右平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）
（4）如图1所示，
是
的边
上的中点，则向量
（ ）
A.
B. 
A
C. 
D. 
D
 |
B C
（5）对于函数
，下列判断正确的是
（ ）
A．周期为
的奇函数 B．周期为
的奇函数
C．周期为
的偶函数 D．周期为的偶函数
（6）若
，且
，则x等于
（ ）
A．
B．
C．
D．
（7）设
是第三象限角，且
，则
所在象限是
（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
（8）在
中，已知角
则角A的值是 （ ）
A．15° B．75° C．105° D．75°或15°
(9)．已知函数f（x）＝
那么
的值为
( )
A．9 B．
C．9
D．
（10）对于任意的两个实数对
和
，规定：
，
当且仅当
；运算“
”为：
；运算“
”为：
，设
，若
，则
（ ）
A．
B． 
C．
D．
二、填空题（共20分，每题4分）
（11）.已知点P分有向线段
的比为－3，那么点P1分
的比是 ．
（12）已知
=（4，8），
=（
，4），且∥，则的值是
（13）已知
＝4，
=2，-2｜＝2，与的夹角为
，则
等于_______．
(14)化简：
=
;
(15)、设
，则
_______
高中一年级比赛考试数学答题卷
一、选择题（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题4分，共20分）
11、 12、
13、 14、 15、
三、解答题（共80分）
16、(本题满分12分)
已知
，求
的值
| 座位号 |
|
|
17、(本题满分12分)
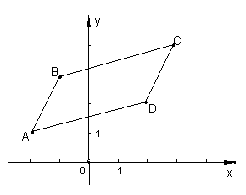
已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2，1)、(-1,3)、(3,4),试求顶点D的坐标。
18、(本题满分14分)
设
（1）求f（x）的值域；
（2）证明f（x）为R上的增函数；
（3）若方程f(x2 –2x-a)＝0在（0，3）上恒有解，求实数a的取值范围。
19、(本题满分14分)
已知向量
，
，
（1）若
求
（2）求
的最大值。
20、(本题满分14分)
设数列
是公比为
的等比数列，
是其前
项和。
（1）若
，求的值；
（2）若
成等差数列，则
是否也成等差数列？证明你的结论。
21、（本题满分14分）
已知函数
(1)写出函数的单调递减区间；
(2)设
，f (x)的最小值是－2，最大值是
，求实数a、b的
高中一年级数学比赛考试数学参考答案
一、选择题（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | C | A | A | B | B | D | B | B |
二、填空题（每小题4分，共20分）
11、
； 12、 2 ； 13、 
； 14、4 ；15、1
三、解答题
16、（12分）解：
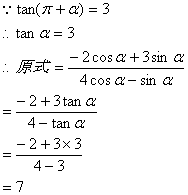
17、(本题满分12分)
解：如图，设顶点D 的坐标为(x,y)------------------------------------------------------------------1分
18、(本题满分14分)
解：（1） （－1，1） （2）略
（3）由于 
∴
由f(x)的单调性知： x2-2x-a=0 x∈(0,3)
∴a=x2-2x x∈(0,3)
=(x-1)2-1 x∈(0,3)
∴ a∈[-1,3)
∴实数a的取值范围为[-1,3]
19、(本题满分14分
解：（1）若 则
………………………………2分
由此得 
（）
所以
……………………………………………………4分
（2）由，，得
，……………………………………………6分
……………………………………8分
=
=
………………11分
∴ 当
时，取得最大值，
即当
时，的最大值为
………………………………13分
20、(本题满分1４分)
解、（1）显然
，由得
得
（2）成等差数列，则
求得
当
时，
不是等差数列
当
时，可以判断满足
故是等差数列
21、（本题满分14分）
(1)解：
4分
∵a＞0，x∈R，∴f (x)的递减区间是
(k∈Z) 6分
(2)解：∵x∈[0，
]，∴2x∈[0，
]，2x－
∈[
] 7分
∴
9分
∴函数f (x)的最小值是
，最大值是
10分
由已知得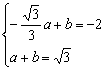
， 解得a＝2，b＝
12分
欢迎访问 http://www.k12zy.com