苍溪中学2007--2008学年度秋季第二学段考试
数学试题(高2010级)
命题人:樊永刚 时间:120分钟 分值:150分
第Ⅰ卷(选择题与填空题)
一、选择题:(本大题共12小题,每小题5分,共60分)将正确答案的番号填入II卷中相应的表格内.
1.若![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.S = T D.
C.S = T D.![]()
2.设函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 、
、![]() 分别为( )
分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知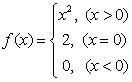 ,则
,则![]() 的值为( )
的值为( )
A.0 B.2 C.4 D.8
4.函数![]() 的值域是( )
的值域是( )
A.![]() B.
B.![]() C.R D.
C.R D.![]()
5.已知命题p:“-2<x<0”,命题q:“x<2”,则![]() p是
p是![]() q的( )
q的( )
A.充分不必要条件 B.既不充分又不必要条件
C.充要条件 D.必要不充分条件
6.函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
A.[6,+![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.方程![]() 的实根个数是( ).
的实根个数是( ).
A.7 B.5 C.3 D.1
8.函数![]() 是定义在
是定义在![]() 上的增函数,且
上的增函数,且![]() ,则下列三个值
,则下列三个值![]() ,
,![]() 间的大小关系是( ).
间的大小关系是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若关于x的不等式ax2+bx+c>0的解集为{x2<x<5},那么不等式cx2-bx-3a<0的解集是( )
A.{x2<x<5}
B.{x![]() <x<1}
C.{x-1<x<
<x<1}
C.{x-1<x<![]() } D.{xx<-1或x>
} D.{xx<-1或x>![]() }
}
10.对于函数![]() ,①图象上一定存在两点,它们的连线平行于x轴。②图象上任意两点的连线都不平行于y轴。③图象关于直线y=x对称。④图象关于原点对称。则这些判断中正确的是( )
,①图象上一定存在两点,它们的连线平行于x轴。②图象上任意两点的连线都不平行于y轴。③图象关于直线y=x对称。④图象关于原点对称。则这些判断中正确的是( )
A. ①③ B.②③ C.②④ D .③
11.函数![]() 在
在![]() 上是减函数,且
上是减函数,且 ![]() 是偶函数,下列不等式成立的是( )
是偶函数,下列不等式成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:E+D=1B,则A×B=( )
A.6E B.
二、填空题:(本大题共4小题,每小题4分,共16分) 将正确答案填入II卷中相应的空格内.
13.已知全集S={1,2,3,4,5,6,7,8,9},A、B都是全集S的子集,且B∩(CSA)={1,9},A∩B={2},(CSA)∩(CSB)={4,6,8},那么A= ;B= 。
14.若关于x 的不等式![]() 的解集为非空集合,那么实数m的取值范围是
。
的解集为非空集合,那么实数m的取值范围是
。
 15.已知函数
15.已知函数![]() ,若
,若![]() ,则
,则![]() 的值为_ _。
的值为_ _。
|
上的图像是一条如图所示的线段(不含点(0,1)),则
不等式![]() 的解集为_
_。
的解集为_
_。
苍溪中学2007--2008学年度秋季第二学段考试
数学试题(高2010级)
命题人:樊永刚 时间:120分钟 分值:150分
第II卷(答题卷)
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
二、填空题(每小题4分,共16分)
13.A= B= ; 14. ;
15.________________ _ ; 16. ;
三、解答题: (共74分)
17.已知![]() 是一个一次函数,且
是一个一次函数,且![]() ,求
,求![]() 的解析式.
的解析式.
18.已知函数![]() .(1)用分段函数的形式表示该函数;
.(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;(3)写出该函数的定义域、值域、奇偶性、单调区间.
19.已知A={x2x-3≤5},B={xx2-5ax+6a2≤0,a>0},求A∩B
20.已知![]()
(1)若![]() ,问k为何值时,g (x)的定义域为R?
,问k为何值时,g (x)的定义域为R?
(2)若f (x)的图象经过原点,求f (x)的解析式;
(3)对于(2)中的f (x),问是否存在实数m、n,使函数y = f
(x),![]() 的值域是
的值域是![]() ?若存在,请求出m、n的值;若不存在,请说明理由.
?若存在,请求出m、n的值;若不存在,请说明理由.
21.经过调查发现,某种新产品在投放市场的100天中,前40天,其价格直线上升,(价格是一次函数),而后60天,其价格则呈直线下降趋势,现抽取其中4天的价格如下表所示:
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格/千元 | 23 | 30 | 22 | 7 |
(1)写出价格f(x)关于时间x的函数表达式(x表示投入市场的第x天);
(2)若销售量g(x)与时间x的函数关系是![]() ,求日销售额的最大值,并求第几天销售额最高?
,求日销售额的最大值,并求第几天销售额最高?
22.设定义在R上的函数f (x),满足当x >0时,f
(x) >1,且对任意![]() ,有
,有![]()
(1)求f (0);
(2)求证:对任意![]() ;
;
(3)解不等式![]() ; (4)解方程
; (4)解方程![]() 。
。
一、选择题:ABCA;DCBB;DBBA。
二、填空题;13.A={2,3,5,7}、B={1,2,9}; 14.R ; 15.0;
16. ![]()
三、17.解:设![]() ,则
,则![]() ………3分
………3分
![]() ………6分
………6分
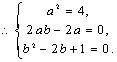 解得
解得![]() ,
,![]() .………10分
.………10分
![]() 或
或![]() .…………12分
.…………12分
20.解:(1)由题意,![]()
∴ ![]() ·············· 4分
·············· 4分
(2)由k – 1 = 0,得k = 1
∴ ![]() ················· 6分
················· 6分
(3)①当![]() 时,f (x)在
时,f (x)在![]() 上递减
上递减
∴ ![]() ,此方程无解.
,此方程无解.
②当n > 1且![]() 时,不可能使结论成立
时,不可能使结论成立
③当n > 1且m < 1时,要使结论成立,则需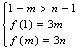 ∴
∴ 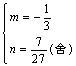
综上,不存在m、n,使结论成立 ·········· 12分
21.解:(1)用待定系数法不难得到
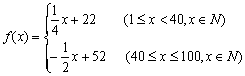 (4分)
(4分)
(2)设日销售额为S千元,
①当1≤x<40时,
②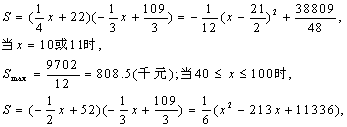 (8分)
(8分)
∴x=40时,Smax=736(千元).(11分)
综上分析,日销售额最高是在第10天或第11天,最高值为808.5千元.(12分)
22.(1)![]() 时,
时,![]() ……3分
……3分
(2)![]() 假设存在某个
假设存在某个![]()
则对任何![]() 与已知矛盾,
与已知矛盾,
![]() ………6分
………6分
(3)任取![]()
![]()
![]()
![]() 为单调递增函数
为单调递增函数 ![]()
![]()
∴不等式的解集为![]() ……………10分
……………10分
(4)![]()
方程![]() 可化为
可化为![]()
即![]() (舍),由(1)得x = 0,
(舍),由(1)得x = 0,
故原方程的解为x = 0. ……………14分
1.已知![]() ,其定义域为
,其定义域为![]() ,
,
(1)当![]() 时,求函数f (x)的值域;(2)当f (x)在定义域内有反函数时,求t 的取值范围.
时,求函数f (x)的值域;(2)当f (x)在定义域内有反函数时,求t 的取值范围.
1.解:(1)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 的值域是
的值域是![]() ……………5分
……………5分
(2)∵f (x)的对称轴是x = t,当t≤0时,f (x)在其定义域内为增函数,
∴此时f (x)有反函数 …………………… 8分
当1≤t<6时,要使f (x)有反函数,应有![]() 即
即![]() ,
,![]()
解之得![]() ……11分
……11分
综上所述,使得f (x)在定义域内有反函数的t的取值范围是t≤0或1≤t<3或![]() …12分
…12分
2.对于任意定义在R上的函数![]() ,若实数
,若实数![]() 满足
满足![]() ,则称
,则称![]() 是函数
是函数![]() 的一个不动点.若二次函数
的一个不动点.若二次函数![]() 没有不动点,则实数
没有不动点,则实数![]() 的取值范围是_____.
的取值范围是_____.
3.方程![]() 有两个不相等的实根x1、x2,且
有两个不相等的实根x1、x2,且![]() ,则k的取值范围是___
,则k的取值范围是___![]() ______.
______.
4.已知偶函数f(x)在![]() 上是增函数,且f(1)=0,则满足xf(x)<0的x的取值的范围为( )
上是增函数,且f(1)=0,则满足xf(x)<0的x的取值的范围为( )
A、(-1,1) B、[-1,1] C、![]() D、
D、![]()
5.已知二次函数![]() 和一次函数
和一次函数![]() ,则“
,则“![]() ”是“这两个函数的图象有两个不同交点”的( )
”是“这两个函数的图象有两个不同交点”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
备注:校平66分,重点班平均88分。整体显得难度非常大。