一. 选择题：本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 设集合U={0，1，2，3，4，5}，集合M={0，3，5}，N={1，4，5}，则
等于（ ）
A. {5} B. {0，3} C. {0，2，3，5} D. {0，1，3，4，5}
2. 命题“
且
”为假，“或”为真，那么（ ）
A.
命题、都是真命题
B.
命题、都是假命题
C.
命题、中仅有一个是真命题
D.
命题、中至少有一个是真命题
3. 下列各组函数中，表示同一个函数的是（ ）
A.
与
B.
与
C.
与
D.
与
（
且
）
4. 函数
的定义域为（ ）
A.
B.
C.
D.
5. 函数
的定义域是
，则其值域是（ ）
A. 
B.
C. 
D.
6. 为了得到函数
的图象，可以把函数
的图象（ ）
A. 向左平移3个单位长度 B. 向右平移3个单位长度
C. 向左平移1个单位长度 D. 向右平移1个单位长度
7. 设
，
，则（ ）
A. 
B. 
C. 
D. 
8. 设
，则数列
、
、
是（ ）
A. 等差数列，但不是等比数列 B. 是等比数列，但不是等差数列
C. 既是等差数列又是等比数列 D. 既不是等差数列又不是等比数列
9. 在等比数列
中，
，若
，则
的值是（ ）
A. 12 B. 10 C. 8 D. 
10. 函数
满足
，
，且
成等差数列，则
的值是（ ）
A.
2 B. 3 C. 2或3 D. 2或
二. 填空题：本大题共6小题，每小题3分，共18分。请将答案填在题中横线上。
11. 计算
的值是
。
12. 已知等差数列的公差是正数，且
，
，则
等于
。
13. 一个正项等比数列的前
项和为
，若
，
，则
等于 。
14. 已知是
的充分不必要条件，
是的必要条件，是的必要条件，那么是成立的
条件。
15. 已知
的反函数为
，若的图象经过点Q（5，2），则等于
。
16. 已知函数满足：对任意实数
，有
，且
，写出一个满足条件的函数，则这个函数可以写为= 。（注：只需写出一个满足条件的函数即可）
三. 解答题：本大题共5小题，共52分。解答应写出文字说明，证明过程或演算步骤。
17.（本小题满分8分）
解不等式
18.（本小题满分10分）
证明函数
在
上是减函数。
19.（本小题满分10分）
（1）（只非重点校做）
已知数列的前项和
求的通项公式、首项、公差。
（2）（只重点校做）
已知数列的前项和，数列
满足
，求的前项和
。
20.（本小题满分12分）
已知二次函数满足条件
和
（1）求的解析式；
（2）求在区间
上的最大值和最小值。
21.（本小题满分12分）
已知数列中
，且
（1）求
；
（2）求数列的通项公式。
【试题答案】
一. 选择题：每小题3分，满分30分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | D | A | A | D | D | A | B | C |
二. 填空题：每小题3分，满分18分。
11. 
12. 2 13. 63 14. 充分不必要条件 15. 1
16. 
（底数在0到1之间的指数函数即可）
三. 解答题：本大题共52分，以下各题为累计得分，其他解法请相应给分。
17.（本小题满分8分）
解：由原不等式得
或
（3分）
∴ 
或
（5分）
∴ 
或
∴ 不等式的解集是
或
（8分）
18.（本小题满分10分）
证明：
（2分）
任取
、
且
（3分）
则
（5分）
∵ 
∴ 
（8分）
∴
即（9分）
∴ 在上是减函数（10分）
19.（本小题满分10分）
（1）（只非重点校做）
（6分），
（8分），
（10分）
（2）（只重点校做）
（4分）
所以当
当
所以当
时，
（6分）
当
时，
（9分）
∴ 
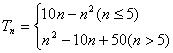（10分）
20.（本小题满分12分）
解：（1）
（6分） （2）最大值3，最小值
（12分）
21.（本小题满分12分）
解：
（1）
，
（4分）
（2）∵ 
∴ 
（8分）
（10分）
（12分）
【试卷分析】
本次数学期末考试依据教学大纲内容，注重基础，考查能力，突出了抽象函数、数列性质、求数列通项公式等重难点问题，这些也是同学们应知应会的内容，所以同学们在平时应该注重基础知识和基本技能的学习和掌握。
【励志故事】
一分钟智慧
风来了，竹子的枝干被风吹弯；风走了，竹子又站得直直的，好像风没来过一样。
云来了，在潭底留下一道影子；云走了，潭底又干干净净的，好像云没来过一样。
竹子不会因为被风吹过，就永远直不起腰来；清澈的潭水，也不会因为云飘过，就永远留住云的影子。
同样的，心胸宽大的人，不会因为别人两句不礼貌的话，就刮起永远的狂风巨浪；也不会因为别人不礼貌的行为，就在心底刻下无法磨灭的伤痕。