新人教A版高二数学同步测试（1）—（2-1第一章）
说明：本试卷分第一卷和第二卷两部分，第一卷74分，第二卷76分，共150分；答题时间120分钟．
一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．
1．函数f（x）=xx+a+b是奇函数的充要条件是 （ ）
A．ab=0 B．a+b=
2．“至多有三个”的否定为 （ ）
A．至少有三个 B．至少有四个 C．有三个 D．有四个
3．有金盒、银盒、铅盒各一个，只有一个盒子里有肖像．金盒上写有命题p：肖像在这个盒子里；银盒上写有命题q：肖像不在这个盒子里；铅盒上写有命题r：肖像不在金盒里．p、q、r中有且只有一个是真命题，则肖像在 （ ）
A．金盒里 B．银盒里
C．铅盒里 D．在哪个盒子里不能确定
4．不等式
对于
恒成立，那么
的取值范围是 （ ）
A．
B．
C．
D．
5．“a和b都不是偶数”的否定形式是 （ ）
A．a和b至少有一个是偶数 B．a和b至多有一个是偶数
C．a是偶数，b不是偶数 D．a和b都是偶数
6．某食品的广告词为：“幸福的人们都拥有”，初听起来，这似乎只是普通的赞美说词，然而他的实际效果大哩，原来这句话的等价命题是 （ ）
A．不拥有的人们不一定幸福 B．不拥有的人们可能幸福
C．拥有的人们不一定幸福 D．不拥有的人们不幸福
7．若命题“p或q”为真，“非p”为真，则 （ ）
A．p真q真 B．p假q真 C．p真q假 D．p假q假
8．条件p：
，
，条件q：
，
，则条件p是条件q的 （ ）
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．即不充分也不必要条件
9．2x2－5x－3＜0的一个必要不充分条件是 （ ）
A．－
＜x＜3 B．－＜x＜ D．－1＜x＜6
10．设原命题：若a+b≥2，则a,b 中至少有一个不小于1．则原命题与其逆命题的真假情况是 （ ）
A．原命题真，逆命题假 B．原命题假，逆命题真
C．原命题与逆命题均为真命题 D．原命题与逆命题均为假命题
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
11．下列命题中_________为真命题．
①“A∩B=A”成立的必要条件是“A
B”；
②“若x2+y2=0，则x，y全为0”的否命题；
③“全等三角形是相似三角形”的逆命题；
④“圆内接四边形对角互补”的逆否命题．
12．若p：“平行四边形一定是菱形”，则“非p”为___ _____．
13．已知p，q都是r的必要条件，s是r的充分条件,q是s的充分条件，则s是q的 条件，r是q的 条件，p是s的 条件．
14．设p、q是两个命题，若p是q的充分不必要条件，那么非p是非q的 条件．
三、解答题：（解答应写出文字说明、证明过程或演算步骤(共76分)．
15．（12分）分别写出下列命题的逆命题，否命题，逆否命题，并判断其真假．
（1）矩形的对角线相等且互相平分；
（2）正偶数不是质数．
16．（12分）写出由下述各命题构成的“p或q”，“p且q”，“非p”形式的复合命题，并指出所构成的这些复合命题的真假．
（1）p：连续的三个整数的乘积能被2整除，q：连续的三个整数的乘积能被3整除；
（2）p：对角线互相垂直的四边形是菱形，q：对角线互相平分的四边形是菱形；
17．（12分）给定两个命题,
：对任意实数
都有
恒成立；
：关于的方程
有实数根；如果与中有且仅有一个为真命题，求实数的取值范围．
18．（12分）已知p，q都是r的必要条件，s是r的充分条件，q是s的充分条件，那么
（1）s是q的什么条件？
（2）r是q的什么条件？
（3）p是q的什么条件？
19．（14分）设0<a, b, c<1，求证：（1－a）b，（1－b）c，（1－c）a不同时大于
．
20．（14分）求证：关于x的方程x2+2ax+b=0 有实数根，且两根均小于2的充分但不必要条件是a≥2且b ≤4.．
参考答案
一、
1．D；解析：若a2+b2=0，即a=b=0时，f（－x）=（－x）x+0+0=－xx=－f（x）
∴a2+b2=0是f（x）为奇函数的充分条件.又若f（x）为奇函数即f（－x）=－x（－x）+a+b=－（xx+a+b），则必有a=b=0，即a2+b2=0，∴a2+b2=0是f（x）为奇函数的必要条件.
2．B；提示：这是一个含有量词的命题的否定．
3．B；本题考查复合命题及真值表．解析：∵p=非r，∴p与r一真一假，而p、q、r中有且只有一个真命题，∴q必为假命题，∴非q：“肖像在这个盒子里”为真命题，即：肖像在银盒里．评述：本题考查充要条件的基本知识，难点在于周期概念的准确把握.
4．B；解析：注意二次项系数为零也可以．
5．A；解析：对“a和b都不是偶数”的否定为“a和b不都不是偶数”，等价于“a和b中至少有一个是偶数”．
6．D；解析：该题考察的是互为逆否命题的真值相同，也就是在选项中找到该命题逆否命题．
7．B；解析：由“非p”为真可得p为假，若同时“p或q”为真，则可得q必须为真．
8．A；解析：由我们学习过的不等式的理论可得
，但
满足q：，，但不满足q，故选项为B．
9．D；解析：由2x2－5x－3＜0，解得－＜x＜3，记为P，则①P
A，②BP，B是P的充分非必要条件，③C
P，C既不是P的充分条件，也不是P的必要条件，④D
P，PD，D是P的必要不充分条件．
10． A；提示：举例：a=1.2，b=0.3，则a+b=1.5<2，∴逆命题为假．
二、
11．②④；
解析：本题是一道开放性题，考查四种命题间的关系及充要条件．
①A∩B=A
A
B但不能得出AB，∴①不正确；
②否命题为：“若x2+y2≠0，则x，y不全为0”，是真命题；
③逆命题为：“若两个三角形是相似三角形，则这两个三角形全等”，是假命题；
④原命题为真，而逆否命题与原命题是两个等价命题，∴逆否命题也为真命题．
12．平行四边形不一定是菱形；或至少有一个平行四边形不是菱形；
解析：本题考查复合命题“非p”的形式，p：“平行四边形一定是菱形”是假命题，这里“一定是”的否定是用“一定不是”还是“不一定是”？若为“平行四边形一定不是菱形”仍为假命题，与真值表相违，故原命题的“非p”为“平行四边形不一定是菱形”，是一个真命题．
第二种说法是命题是全称命题的简写形式，应用规则变化即可．
13．必要，充分，必要．
提示：画出箭头图．
14．必要不充分．
三、
15．本题考查四种命题间的关系．
解：（1）逆命题：若一个四边形的对角线相等且互相平分，则它是矩形（假命题）．
否命题：若一个四边形不是矩形，则它的对角线不相等或不互相平分（假命题）．
逆否命题：若一个四边形的对角线不相等或不互相平分，则它不是矩形（真命题）．
（2）逆命题：如果一个正数不是质数，那么这个正数是正偶数（假命题）．
否命题：如果一个正数不是偶数，那么这个数是质数（假命题）．
逆否命题：如果一个正数是质数，那么这个数不是偶数（假命题）．
16．解：（1）根据真值表，复合命题可以写成简单形式：
p或q：连续的三个整数的乘积能被2或能被3整除.
p且q：连续的三个整数的乘积能被2且能被3整除.
非p：存在连续的三个整数的乘积不能被2整除.
∵连续的三整数中有一个（或两个）是偶数，而有一个是3的倍数，
∴p真，q真，∴p或q与p且q均为真，而非p为假.
（2）根据真值表，只能用逻辑联结词联结两个命题，不能写成简单形式：
p或q：对角线互相垂直的四边形是菱形或对角线互相平分的四边形是菱形.
p且q：对角线互相垂直的四边形是菱形且对角线互相平分的四边形是菱形.
非p：存在对角线互相垂直的四边形不是菱形.
∵p假q假，∴p或q与p且q均为假，而非p为真.
17．解：对任意实数都有恒成立
；关于的方程
有实数根
；如果P正确，且Q不正确，有
；如果Q正确，且P不正确，有
．所以实数的取值范围为
．
18．本题考查充要条件、充分条件、必要条件．对于这类问题，将语言叙述符号化，画出它们的综合结构图，再给予判定．
解：p、q、r、s的关系如图所示，由图可知
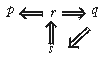
答案：（1）s是q的充要条件 （2）r是q的充要条件 （3）p是q的必要条件
19．证明：用反证法，假设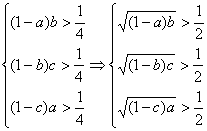
，①+②+③得：
，左右矛盾，故假设不成立，∴（1－a）b,（1－b）c，（1－c）a不同时大于.
20．解析：先证充分性，而必要性只需要通过举反例来否定.
先证明条件的充分性：
|
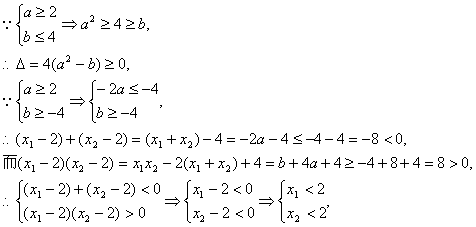
①、②知“a≥2且b≤4” 
“方程有实数根，且两根均小于2”.
再验证条件不必要：
∵方程x2－x=0的两根为x1=0, x2=1，则方程的两根均小于2，而a=－
<2，
∴“方程的两根小于2” “a≥2且b≤4”.
综上，a≥2且b≤4是方程有实数根且两根均小于2的充分但不必要条件.
评析：充分条件与必要条件是数学学习中的重要概念，在解答任何一个数学问题时都必须准确认识到问题所需要解决的是满足条件的充分性、必要性，还是充分且必要.对于证明题、计算题等，往往只需满足命题条件的充分性，即由条件进行推理、演绎得出结论；而对于求参数的范围，求不等式的解集，求函数的值域等许多问题，则必需保证推理的充要性.