高二数学同步测试10

新课标高二数学同步测试（10）—（2－2）

说明：本试卷分第一卷和第二卷两部分，第一卷74分，第二卷76分，共150分；答题时间120分钟．

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

1．函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　B．　　　　　　　C．　　　　　 D．

2．函数的值域为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　B．　　　　　　C． 　　 D．

3．若复数z的共轭复数是，且z=1，则(z+1)(z-i)的最大值是　　　（　　）

　　　 A．2+　 　　　　 B．2-　　　　　 C．1+　　　　　D．3+

4．复数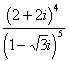等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B．－　　　　　 C．　　　　　　　D．－

5．设f(x)=log_ax(a﹥0,a≠1),若f(x₁)+f(x₂)+……＋f(x_n)=1(x_i∈R^＋,i=1、2……n),则f(x₁²)＋f(x₂²)＋……＋f(x_n²)的值等于　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　B．1 　　　　　　　　　C．2　　　 　　　　　　D．2log_a2

6． =　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1　 　　　　　　　　 B．－1 　　　　　　　C．i　　　　　　　　　 D．－i

7．求曲线，所围成图形的面积　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　 　　　　　　　　 B．　　　　　　　　 C．9 　　　　　　　　　　　D．

8．设，则满足等式的复数Z对应的点的轨迹是：（　　）

　　　 A．椭圆　　　　　　　　　 B．双曲线　　　　　　　　C．抛物线　　　　　　　 D．圆

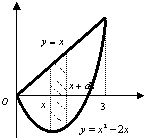
9．在抛物线上找一点P，其中，过点P作抛物线的切线，使此切线与抛物线及两坐标轴所围平面图形的面积最小　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　 B．　　　　 C．　　　　　　D．

10．已知复数z_k(k=1，2，3，…，101)满足z_k=1，命题甲为：=0，命题乙：复平面内以z_k(k=1，2，3，…，101)的对应点为顶点的101边形是正多边形，那么命题甲是命题乙的　　　　　　　　　　　　　　　　　　　　　（ 　 ）

　　　 A．充分不必要条件 　　　　　　　　　　　　　　　 B．必要不充分条件　

　　　 C．充分且必要条件 　　　　　　　　　　　　　　　 D．既不充分不必要条件

二、填空题：请把答案填在题中横线上（每小题6分，共24分）．

11．已知，奇函数在上单调，则字母应满足的条件是　　　　　　　　　  ．

12．某日中午12时整，甲船自A处以16km/h的速度向正东行驶，乙船自A的正北18km处以24km/h的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率　　  km/h.．

13．=　　　　　　　　　  ．

14．已知两条相交直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点点，五条直线最多有10个交点．由此可归纳n条直线最多交点个数为 　　　　　　　 ．

三、解答题：解答应写出文字说明、证明过程或演算步骤（共76分）．

15．（12分）已知复数

　　　 根据下列条件，求m值．

　　　 （1）z是实数；（2）z是虚线；（3）z是纯虚数；（4）z＝0．

16．（12分）用活塞封闭圆柱钢筒中的理想气体，气体膨胀时推动活塞．设气体体积从V₀膨胀到V₁，且膨胀时温度不变，求气体压力对活塞所作功．

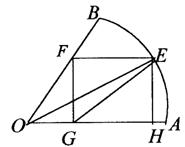
17．（12分）如图，扇形AOB的半径为1，中心角为45°，矩形EFGH内接于扇形，求矩形对角线长的最小值．

18．（12分）已知数列为其前n项和，计算得,,观察上述结果，推测出计算S_n的公式，并用数学归纳法加以证明．

19．（14分）如图所示，曲线段OMB是函数f(x)＝x²(0＜x＜6＝的图象，BA⊥x轴于A，曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P，交线段AB于Q，⑴试用t表示切线PQ的方程；⑵试用t表示出△QAP的面积g(t)；若函数g(t)在(m，n)上单调递减，试求出m的最小值；⑶若S_△QAP∈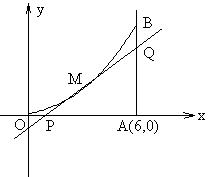[]，试求出点P横坐标的取值范围

20．（14分）已知函数满足下列条件：对任意的实数x₁，x₂都有　和，其中是大于0的常数.设实数a₀，a，b满足 和.

　　　 （Ⅰ）证明:，并且不存在，使得；

　　　 （Ⅱ）证明:；

　　　 （Ⅲ）证明:.

参考答案

一、1．C；2．C；3．A；

4．解法一：

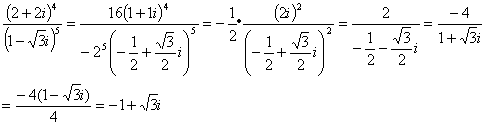
答案：选B

5．C

6．B；解析：

7．C；解：联立：，解的交点：、

，

且，

或者直接利用推出的公式，此时，，，则

8．C；9．C；

分析：此是一道综合应用题，应先求出所求面积的表达式，然后求此表达式函数的极值点．

解：由于，因此过点P的切线方程为，该切线与，轴的交点分别是，.

所求面积A==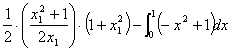

.

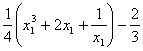
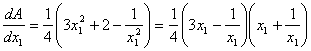令．(由于)得， 由于此问题的最小值存在，且在内有唯一驻点，故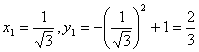就是所求的点P，即：取切点为P时，所求的图形面积最小．

10．B

二、11．；

解析：；．，
若上是增函数，则恒成立，即
若上是减函数，则恒成立，这样的不存在．
综上可得：；

12．；13．；解析：．

14．．

三、15．解：

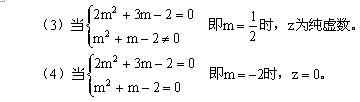
　　注：对于本题，只要概念清晰，就能顺利地列出以上各式，求出m值．

16．解 设圆柱钢筒的底面积为S，dV为气体体积之增量，此时活塞移动的距离为，由于是等温过程，由定律知：为常量)．因此，气体作用于活塞大单位面积上的压力（即压强）为，此时，活塞所受的总压力是，所以所以气体体积增加dv时，气体压力所作的功为，由此得到，当气体体积从V₀变到V₁时作的功是．　　

17．[解析]这是一道高考题，需要用函数思想解决它，但是取什么量作自变量是解决这个问题的关键，应反复斟酌. 根据这个问题的图形特点，取将对角线长表示成这个角的函数是比较好的想法.

 

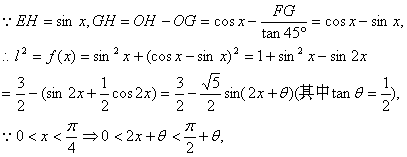
所以，当时，

[解法二]设矩形的高

　∴矩形的宽

 ∴对角线

　令

　

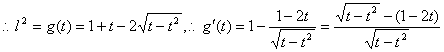
　令

　在的左、右两侧取定义域内两点，如取

　得

　　　 ∴的值在处左负右正，

.

 [评析]该问题的难点是正确选择自变量,上面两种解法各有优缺点,解法一虽然简单些,但选择”角”作自变量有时会涉及到过多的三角知识,在许多情况下会出现困难的运算,应慎重;解法二选择矩形的边长为自变量的想法要常规一些.

18．解：推测.

证明：i) 略

ii) 假设n=k(k∈N)时等式成立，即，

则

　　　

　　　

　　　

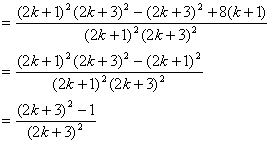
即 n=k+1时，等式成立．

由i), ii) 可知，对一切n∈N，等式均成立．

小结：这是一个探索性问题，需要观察（归纳），从而发现规律，得出结论，进而用数学归纳法．

19．【解】：⑴设点M(t，t²)，又f＇(x)=2x，

∴过点M的切线PQ的斜率k=2t　　 ∴切线PQ的方程为：y=2tx－t²

⑵由⑴可求得，P()，Q(6,12t－t²)∴g(t)＝S_△QAP＝(12t－t²)=(0<t<6)

由于g＇(t)=,令g＇(t)<0，则4<t<12，考虑到0<t<6,∴4<t<6，

∴函数g(t)的单调递减区间是(4,6)，因此m的最小值为4

⑶由⑵知，g(t)在区间(4,6)上递减，∴此时S_△QAP∈(g(6)，g(4))=(54,64)

令g＇(t)＞0，则0<t<4，∴g(t) 在区间(0，4)上递增，

S_△QAP∈(g(0)，g(4))=(0，64)，又g(4)＝64

∴g(t)的值域为(0，64)

由≤g(t)≤64，得1≤t<6∴≤<3，∴点P的横坐标∈[,3]

20．证明：（Ⅰ）不妨设，由

可知，是R上的增函数不存在，使得

又

（Ⅱ）要证：

即证：.　　　　　　　　 

不妨设，由得.

即.则.　　　（1）

由得. 即.

则. 　　 （2）

由（1）（2）可得.

（Ⅲ）,,

又由（2）中结论..