高二数学同步测试2

　　　　　　　

新课标高二数学同步测试（2）—（2－1第二章2.1－2.3）

说明：本试卷分第一卷和第二卷两部分，第一卷74分，第二卷76分，共150分；答题时间120分钟．

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

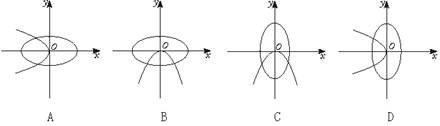
1．在同一坐标系中，方程a²x²+b²y²=1与ax+by²=0（a＞b＞0）的曲线大致是　　　　 （　　）

2．已知椭圆和双曲线＝1有公共的焦点，那么双曲线的渐近线方程是　　　　　　　　　　　（　　）

　　A．x＝±　　 B．y＝± 　　C．x＝±　　　 D．y＝±

3．过抛物线y=ax²（a＞0）的焦点F用一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．2a　　　　　　　　　　　B．　　　　　　　　　　C．4a　　　 　　　　　D．

4．若椭圆的左、右焦点分别为F₁、F₂，线段F₁F₂被抛物线y₂=2bx的焦点分成5：3两段，则此椭圆的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．　　　 　　　　B．　 　　　　　C．　　  　　　　　 D．

5．椭圆=1的一个焦点为F₁，点P在椭圆上.如果线段PF₁的中点M在y轴上，那么点M的纵坐标是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．±　　　　　　B．±　　　　　　　　C．±　　　　　　　 D．±

6．设F₁和F₂为双曲线y²＝1的两个焦点，点P在双曲线上，且满足∠F₁PF₂＝90°，则△F₁PF₂的面积是　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．1　　　　　　　　　　　　B． 　　　　　　　　 C．2　　　　　　　　　　　　D．

7．已知F₁、F₂是两个定点，点P是以F₁和F₂为公共焦点的椭圆和双曲线的一个交点，并且PF₁⊥PF₂，e₁和e₂分别是椭圆和双曲线的离心率，则有　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　　　　　B．　　　 C．　 D．

8．已知方程+=1表示焦点在y轴上的椭圆，则m的取值范围是　　　（　　）

　　A．m<2　　　　　　　　　 　　　　　　　　　　　　　　　　B．1<m<2

　　C．m<－1或1<m<2　　　　　　　　　　　　　　　　D．m<－1或1<m<

9．已知双曲线－=1和椭圆+=1(a>0,m>b>0)的离心率互为倒数，那么以a、b、m为边长的三角形是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．锐角三角形　　　　　　　　　　　　　　　　　　　　B．直角三角形

　　C．钝角三角形　　　　　　　　　　　　　　　　　　　　D．锐角或钝角三角形

10．椭圆上有n个不同的点: P₁, P₂, …, P_n, 椭圆的右焦点为F. 数列｛P_nF｝是公差大于的等差数列, 则n的最大值是　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．198　　　　　　　　　B．199 　　　　　　　　C．200　　 　　　　　　D．201

二、填空题：请把答案填在题中横线上（每小题6分，共24分）．

11．已知点（－2，3）与抛物线y²=2px（p＞0）的焦点的距离是5，则p=___　　  __．

12．设圆过双曲线=1的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是　　　　　　．

13．双曲线＝1的两个焦点为F₁、F₂，点P在双曲线上，若PF₁⊥PF₂，则点P到x轴的距离为　 　　　　 ．

14．若A点坐标为（1，1），F₁是5x²＋9y²=45椭圆的左焦点，点P是椭圆的动点，则PA＋P F₁的最小值是_______　　___．

三、解答题：解答应写出文字说明、证明过程或演算步骤（共76分）．

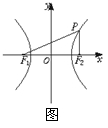15．（12分）已知F₁、F₂为双曲线（a＞0，b＞0）的焦点，过F₂作垂直于x轴的直线交双曲线于点P，且∠PF₁F₂＝30°．求双曲线的渐近线方程．

16．（12分）已知椭圆的长、短轴端点分别为A、B，从此椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量与是共线向量．

（1）求椭圆的离心率e；

（2）设Q是椭圆上任意一点， 、分别是左、右焦点，求∠ 的取值范围；

17．（12分）如图椭圆 (a>b>0)的上顶点为A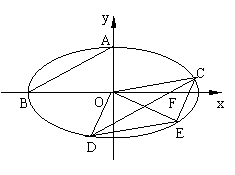，左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上．

（Ⅰ）求椭圆的离心率；

　　　 （Ⅱ）若平行四边形OCED的面积为, 求椭圆方程．

18．（12分）双曲线 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(－1,0)到直线l的距离之和s≥c.求双曲线的离心率e的取值范围．

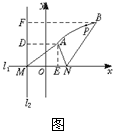
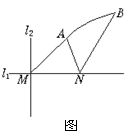19．（14分）如图，直线l₁和l₂相交于点M，l₁⊥l₂，点N∈l₁.以A、B为端点的曲线段C上的任一点到l₂的距离与到点N的距离相等.若△AMN为锐角三角形，AM=，AN=3，且BN=6.建立适当的坐标系，求曲线段C的方程

20．（14分）已知圆C₁的方程为(x－2)²+(y－1)²=，椭圆C₂的方程为+=1（a>b>0），C₂的离心率为，如果C₁与C₂相交于A、B两点，且线段AB恰为圆C₁的直径，求直线AB的方程和椭圆C₂的方程．

参考答案

一、1．D；解析一：将方程a²x²+b²y²=1与ax+by²=0转化为标准方程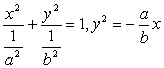：.因为a＞b＞0，因此，＞0，所以有：椭圆的焦点在y轴，抛物线的开口向左，得D选项.

解析二：将方程ax+by²=0中的y换成－y，其结果不变，即说明：ax+by²=0的图形关于x轴对称，排除B、C，又椭圆的焦点在y轴.故选D.

评述：本题考查椭圆与抛物线的基础知识，即标准方程与图形的基本关系.同时，考查了代数式的恒等变形及简单的逻辑推理能力.

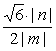2．D；解析：由双曲线方程判断出公共焦点在x轴上，∴椭圆焦点（，0），双曲线焦点（，0），∴3m²－5n²=2m²+3n²∴m²=8n²又∵双曲线渐近线为y=±·x∴代入m²=8n²，m=2n，得y=±x．

3．C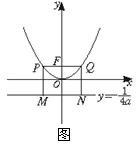；解析：抛物线y=ax²的标准式为x²＝y，∴焦点F（0，）.

取特殊情况，即直线PQ平行x轴，则p=q.

如图，∵PF＝PM，∴p＝，故．

4．D；

5．A；解析：由条件可得F₁（－3，0），PF₁的中点在y轴上，∴P坐标（3，y₀），又P在=1的椭圆上得y₀=±，∴M的坐标（0，±），故选A.

评述：本题考查了椭圆的标准方程及几何性质，中点坐标公式以及运算能力.

6．A；解法一：由双曲线方程知F₁F₂＝2，且双曲线是对称图形，假设P（x，），由已知F₁P⊥F₂ P，有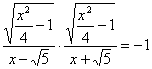，即，因此选A.

评述：本题考查了双曲线的标准方程及其性质、两条直线垂直的条件、三角形面积公式以及运算能力.

7．D；

8．D；

9．B；

10．C；

二、

11．4；解析：∵抛物线y²=2px（p＞0）的焦点坐标是（，0），由两点间距离公式，得=5．解得p=4.

12．；解析：如图8—15所示，设圆心P（x₀，y₀），则x₀＝＝4，代入＝1，得y₀²＝，∴OP＝．

评述：本题重点考查双曲线的对称性、两点间距离公式以及数形结合的思想.

13．；解析：设PF₁＝M，PF₂＝n（m＞n），a＝3、b＝4、c＝5，∴m－n＝６  m²＋n²＝4c²，m²＋n²－（m－n）²＝m²＋n²－（m²＋n²－2mn）＝2mn＝4×25－36＝64，mn＝32.

又利用等面积法可得：2c·y＝mn，∴y＝．

14．；

三、

15．解：（1）设F₂（c，0）（c＞0），P（c，y₀），则=1．解得y₀=±，

∴PF₂=，在直角三角形PF₂F₁中，∠PF₁F₂=30°

解法一：F₁F₂=PF₂，即2c=，将c²=a²+b²代入，解得b²=2a²

解法二：PF₁=2PF₂，由双曲线定义可知PF₁－PF₂=2a，得PF₂=2a.

∵PF₂=，∴2a=，即b²=2a²，∴

故所求双曲线的渐近线方程为y=±x．

16．解：（1）∵，∴．

∵是共线向量，∴，∴b=c,故．

（2）设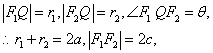

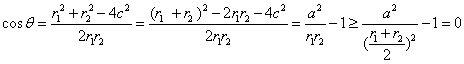
当且仅当时，cosθ=0，∴θ．

说明：由于共线向量与解析几何中平行线、三点共线等具有异曲同工的作用，因此，解析几何中与平行线、三点共线等相关的问题均可在向量共线的新情景下设计问题．求解此类问题的关键是：正确理解向量共线与解析几何中平行、三点共线等的关系，把有关向量的问题转化为解析几何问题．

17．解：(Ⅰ) ∵焦点为F(c, 0), AB斜率为, 故CD方程为y=(x－c). 于椭圆联立后消去y得2x²－2cx－b²=0. ∵CD的中点为G(), 点E(c, －)在椭圆上, ∴将E(c, －)代入椭圆方程并整理得2c²=a², ∴e =.

(Ⅱ)由(Ⅰ)知CD的方程为y=(x－c),  b=c, a=c. 与椭圆联立消去y得2x²－2cx－c²=0.

 ∵平行四边形OCED的面积为

S=cy_C－y_D=c=c,

∴c=, a=2, b=. 故椭圆方程为

18．解：直线l的方程为bx+ay－ab=0.由点到直线的距离公式,且a>1,得到点(1,0)到直线l的距离d₁ =．

同理得到点(－1,0)到直线l的距离d₂ =.s= d₁ +d₂==.

由s≥c,得≥c,即5a≥2c².

于是得5≥2e².即4e²－25e+25≤0.解不等式,得≤e²≤5.

由于e>1>0,所以e的取值范围是.

19．解法一：如图建立坐标系，以l₁为x轴，MN的垂直平分线为y轴，点O为坐标原点.

依题意知：曲线段C是以点N为焦点，以l₂为准线的抛物线的一段，其中A、B分别为C的端点.

设曲线段C的方程为，y²=2px（p＞0），（x_A≤x≤x_B，y＞0）

其中x_A、x_B分别为A、B的横坐标，p＝MN．所以M（，0），N（，0）

由AM＝，AN＝3得：

（x_A＋）²＋2px_A＝17　　　　　　 ①

（x_A）²＋2px_A＝9　　　　　　　 ②

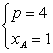由①②两式联立解得x_A＝，再将其代入①式并由p>0，解得或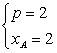

因为△AMN是锐角三角形，所以＞x_A，故舍去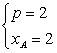

所以p＝4，x_A＝1．由点B在曲线段C上，得x_B＝BN＝4．

综上得曲线段C的方程为y²＝8x（1≤x≤4，y＞0）．

解法二：如图建立坐标系，分别以l₁、l₂为x、y轴，M为坐标原点.作AE⊥l₁，AD⊥l₂，BF⊥l₂，垂足分别为E、D、F.设A（x_A，y_A）、B（x_B，y_B）、N（x_N，0）

依题意有x_A＝ME＝DA＝AN＝3，y_A＝DM＝

由于△AMN为锐角三角形，故有

x_N＝ME＋EN＝ME＋＝4，x_B＝BF＝BN＝6．

设点P（x，y）是曲线段C上任一点，则由题意知P属于集合

｛（x，y）（x－x_N）²+y²=x²，x_A≤x≤x_B，y＞0｝

故曲线段C的方程为y²＝8（x－2）（3≤x≤6，y＞0）．

评述：本题考查根据所给条件选择适当的坐标系，求曲线方程的解析几何的基本思想，考查了抛物线的概念和性质、曲线和方程的关系以及综合运用知识的能力.

20．由e=，得=，a²=2c²,b²=c²．

设椭圆方程为+=1．又设A(x₁,y₁),B(x₂,y₂)．由圆心为(2,1)，得x₁+x₂=4,y₁+y₂=2．

又+=1，+=1，两式相减，得 +=0．

∴

∴直线AB的方程为y－1= －(x－2)，即y= －x+3．

将y= －x+3代入+=1，得3x²－12x+18－2b²=0

又直线AB与椭圆C₂相交，∴Δ=24b²－72>0．

由AB=x₁－x₂==,得·=．

解得　b²=8，故所求椭圆方程为+=1．