新课标高二数学同步测试(3)—(2-1第二章2.4-2.5)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.x=![]() 表示的曲线是 ( )
表示的曲线是 ( )
A.双曲线 B.椭圆
C.双曲线的一部分 D.椭圆的一部分
2.设双曲线![]() =1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为
=1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为![]() c,则双曲线的离心率为 ( )
c,则双曲线的离心率为 ( )
A.2 B.![]() C.
C.![]() D.
D.![]()
3.中心在原点,焦点坐标为(0, ±5![]() )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为![]() ,则椭圆方程为 ( )
,则椭圆方程为 ( )
A.![]() +
+![]() =1 B.
=1 B.![]() +
+![]() =
=![]() +
+![]() =1 D.
=1 D.![]() +
+![]() =1
=1
4.过双曲线![]() 的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有 ( )
的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有 ( )
A.1条 B.2条 C.3条 D.4条
5.过椭圆![]() +
+![]() =1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是 ( )
=1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是 ( )
A.ab B.ac C.bc D.b2
6.椭圆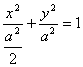 与连结A(1,2),B(2,3)的线段没有公共点,则正数a的取值范围是( )
与连结A(1,2),B(2,3)的线段没有公共点,则正数a的取值范围是( )
A.(0,![]() )∪ (
)∪ (![]() ,∞) B.(
,∞) B.(![]() ,∞)
,∞)
C.[![]() ,
,![]() ] D.(
] D.(![]() ,
,![]() )
)
7.以椭圆的右焦点F2为圆心的圆恰好过椭圆的中心,交椭圆于点M、N,椭圆的左焦点为
F1,且直线MF1与此圆相切,则椭圆的离心率e为 ( )
A.![]() B.
B.![]() C
.2-
C
.2-![]() D.
D.![]() -1
-1
8.已知F1, F2是双曲线的两个焦点, Q是双曲线上任意一点, 从某一焦点引∠F1QF2平分线的垂线, 垂足为P, 则点P的轨迹是 ( )
A.直线 B.圆 C.椭圆 D.双曲线
9.已知抛物线y=2x2上两点A(x1,y1), B(x2,y2)关于直线y=x+m对称, 且x1x2=-![]() , 那么m的值等于 ( )
, 那么m的值等于 ( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
10.对于抛物线C: y2=4x, 我们称满足y02<4x0的点M(x0, y0)在抛物线的内部, 若点M(x0, y0)在抛物线的内部, 则直线l: y0y=2(x+ x0)与C ( )
A.恰有一个公共点 B.恰有二个公共点
C.有一个公共点也可能有二个公共点 D.没有公共点
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.椭圆x2+4y2=4长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是 .
12.设P为双曲线![]() y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 .
y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 .
13.定长为l (l>![]() )的线段AB的端点在双曲线b2x2-a2y2=a2b2的右支上, 则AB中点M的横坐标的最小值为
)的线段AB的端点在双曲线b2x2-a2y2=a2b2的右支上, 则AB中点M的横坐标的最小值为
14.如果过两点![]() 和
和![]() 的直线与抛物线
的直线与抛物线![]() 没有交点,那么实数
没有交点,那么实数![]() 的取值范围是_____________.
的取值范围是_____________.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知抛物线y2=8x上两个动点A、B及一个定点M(x0, y0),F是抛物线的焦点,且AF、MF、BF成等差数列,线段AB的垂直平分线与x轴交于一点N.
(1)求点N的坐标(用x0表示);
(2)过点N与MN垂直的直线交抛物线于P、Q两点,若MN=4![]() ,求△MPQ的面积.
,求△MPQ的面积.
16.(12分)已知双曲线![]() 的离心率
的离心率![]() ,过
,过![]() 的直线到原点的距离是
的直线到原点的距离是![]()
(1)求双曲线的方程;
(2)已知直线![]() 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
17.(12分)已知抛物线![]() 的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
|
18.(12分)已知抛物线、椭圆和双曲线都经过点![]() ,它们在
,它们在![]() 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这三条曲线的方程;
(2)已知动直线![]() 过点
过点![]() ,交抛物线于
,交抛物线于![]() 两点,是否存在垂直于
两点,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
19.(14分)设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
20.(14分)已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() 共线.
共线.
(1)求椭圆的离心率;
(2)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值.
为定值.
参考答案
一、1.D;解析:x=![]() 化为x2+3y2=1(x>0).
化为x2+3y2=1(x>0).
2.A;解析:由已知,直线l的方程为ay+bx-ab=0,原点到直线l的距离为![]() c,则有
c,则有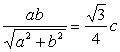 ,又c2=a2+b2,∴4ab=
,又c2=a2+b2,∴4ab=![]() c2,两边平方,得
c2,两边平方,得![]() .而0<a<b,得e2=
.而0<a<b,得e2=![]() >2,∴e2=4.故e=2.评述:本题考查点到直线的距离,双曲线的性质以及计算、推理能力.难度较大,特别是求出e后还须根据b>a进行检验.
>2,∴e2=4.故e=2.评述:本题考查点到直线的距离,双曲线的性质以及计算、推理能力.难度较大,特别是求出e后还须根据b>a进行检验.
3.C;4.C;5.C;6.A;7.D;8.B;9.B;10.D
二、
11.![]() ;解析:原方程可化为
;解析:原方程可化为![]() +y2=1,a2=4,b2=1,∴a=2,b=1,c=
+y2=1,a2=4,b2=1,∴a=2,b=1,c=![]() .当等腰直角三角形,设交点(x,y)(y>0)可得2-x=y,代入曲线方程得:y=
.当等腰直角三角形,设交点(x,y)(y>0)可得2-x=y,代入曲线方程得:y=![]() ∴S=
∴S=![]() ×2y2=
×2y2=![]() .
.
12.x2-4y2=1;解析:设P(x0,y0)∴M(x,y),∴![]() ∴2x=x0,2y=y0
∴2x=x0,2y=y0
∴![]() -4y2=1
-4y2=1![]() x2-4y2=1.
x2-4y2=1.
13.![]() ;
;
14.![]() ;
;
三、
15.(1)设A(x1, y1)、B(x2、y2),由AF、MF、BF成等差数列得x1+x2=2x0.
得线段AB垂直平分线方程:![]()
令y=0,得x=x0+4, 所以N(x0+4, 0).
(2)由M(x0,
y0) , N(x0+4,
0), MN=4![]() , 得x0=2.
, 得x0=2.
由抛物线的对称性,可设M在第一象限,所以M(2, 4), N(6,0).
直线PQ: y=x-6, 由 得△MPQ的面积是64.
得△MPQ的面积是64.
16.解:∵(1)![]() 原点到直线AB:
原点到直线AB:![]() 的距离
的距离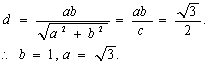 .
.
故所求双曲线方程为 ![]()
(2)把![]() 中消去y,整理得
中消去y,整理得 ![]() .
.
设![]() 的中点是
的中点是![]() ,则
,则
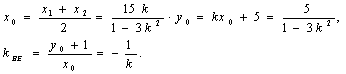
![]()
即![]()
故所求k=±![]() .
.
说明:为了求出![]() 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构![]() 的方程.
的方程.
17.解:设![]() 、
、![]() ,中点
,中点![]()
当AB直线的倾斜角90°时,AB直线方程是![]() (2分)
(2分)
当AB直线的倾斜角不为90°时,![]() 相减得
相减得![]()
所以![]() (4分)
(4分)
设AB直线方程为:![]() ,由于弦AB与直线y=1有公共点,故当y=1时,
,由于弦AB与直线y=1有公共点,故当y=1时,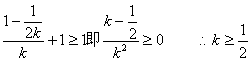
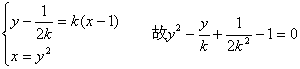
所以![]() ,
,
故![]()
![]()
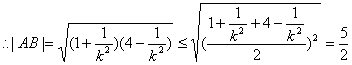
故当![]()
18.解:(Ⅰ)设抛物线方程为![]() ,将
,将![]() 代入方程得
代入方程得![]() ,
,
![]() ;
;
由题意知椭圆、双曲线的焦点为![]() ;
;
对于椭圆,![]() ;
;
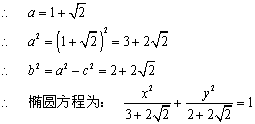
对于双曲线,![]()
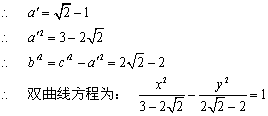
(2)设![]() 的中点为
的中点为![]() ,
,![]() 的方程为:
的方程为:![]() ,以
,以![]() 为直径的圆交
为直径的圆交![]() 于
于![]() 两点,
两点,![]() 中点为
中点为![]()
令![]()
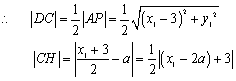
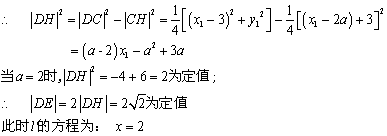
19.解:(1)椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得![]() )在椭圆上,因此
)在椭圆上,因此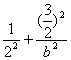 =1得b2=3,于是c2=1.
=1得b2=3,于是c2=1.
所以椭圆C的方程为![]() =1,焦点F1(-1,0),F2(1,0).
=1,焦点F1(-1,0),F2(1,0).
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:
![]() , 即x1=2x+1,y1=2y.
, 即x1=2x+1,y1=2y.
因此![]() =1.即
=1.即![]() 为所求的轨迹方程.
为所求的轨迹方程.
(3)类似的性质为:若M、N是双曲线:![]() =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.
=1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.
设点M的坐标为(m,n),则点N的坐标为(-m,-n),其中![]() =1.
=1.
又设点P的坐标为(x,y),由![]() ,
,
得kPM·kPN=![]() ,将
,将![]() m2-b2代入得kPM·kPN=
m2-b2代入得kPM·kPN=![]() .
.
评述:本题考查椭圆的基本知识,求动点轨迹的常用方法.第(3)问对考生的逻辑思维能力、分析和解决问题的能力及运算能力都有较高的要求,根据提供的信息,让考生通过类比自己找到所证问题,这是高考数学命题的方向,应引起注意
20.本小题主要考查直线方程、平面向量及椭圆的几何性质等基本知训,考查综合运用数学知识解决问题及推理的能力.
(1)解:设椭圆方程为![]()
则直线AB的方程为![]()
化简得![]() .
.
令![]() 则
则 ![]()
![]()
![]() 共线,得
共线,得
![]()
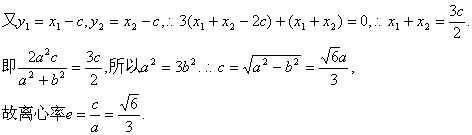
(2)证明:由(I)知![]() ,所以椭圆
,所以椭圆![]() 可化为
可化为![]() .
.
![]()
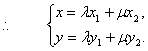
![]() 在椭圆上,
在椭圆上,
![]()
即 ![]() ①
①
由(1)知![]()
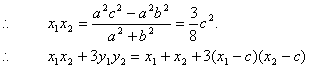
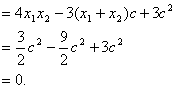
又![]() 又,代入①得
又,代入①得 ![]()
故![]() 为定值,定值为1.
为定值,定值为1.