新课标高二数学同步测试(4)—(2-1第三章3.1)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
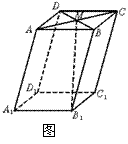 1.在平行六面体ABCD—A1B
1.在平行六面体ABCD—A1B![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .则下列向量中与
.则下列向量中与![]() 相等的向量是( )
相等的向量是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.在下列条件中,使M与A、B、C一定共面的是 ( )
A.![]() B.
B.![]()
C.![]()
![]() D.
D.![]()
![]()
3.已知平行六面体![]() 中,AB=4,AD=3,
中,AB=4,AD=3,![]() ,
,![]() ,
,![]() ,则
,则![]() 等于 ( )
等于 ( )
A.85 B.![]() C.
C.![]() D.50
D.50
4.与向量![]() 平行的一个向量的坐标是 ( )
平行的一个向量的坐标是 ( )
A.(![]() ,1,1) B.(-1,-3,2)
,1,1) B.(-1,-3,2)
C.(-![]() ,
,![]() ,-1) D.(
,-1) D.(![]() ,-3,-2
,-3,-2![]() )
)
5.已知A(-1,-2,6),B(1,2,-6)O为坐标原点,则向量![]() 的夹角是( )
的夹角是( )
A.0 B.![]() C.
C.![]() D.
D.![]()
6.已知空间四边形ABCD中,![]() ,点M在OA上,且OM=2MA,N为BC中点,则
,点M在OA上,且OM=2MA,N为BC中点,则![]() = ( )
= ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.设A、B、C、D是空间不共面的四点,且满足![]() ,则DBCD是 ( )
,则DBCD是 ( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.不确定
8.空间四边形OABC中,OB=OC,ÐAOB=ÐAOC=600,则cos![]() = ( )
= ( )
A.![]() B.
B.![]() C.-
C.-![]() D.0
D.0
9.已知A(1,1,1)、B(2,2,2)、C(3,2,4),则![]() ABC的面积为 ( )
ABC的面积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 已知![]() ,则
,则![]() 的最小值为 ( )
的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.若![]() ,
,![]() ,则
,则![]() 为邻边的平行四边形的面积为
.
为邻边的平行四边形的面积为
.
12.已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且![]() ,现用基组
,现用基组![]() 表示向量
表示向量![]() ,有
,有![]() =x
=x![]() ,则x、y、z的值分别为 .
,则x、y、z的值分别为 .
13.已知点A(1,-2,11)、B(4,2,3),C(6,-1,4),则DABC的形状是 .
14.已知向量![]() ,
,![]() ,若
,若![]() 成1200的角,则k= .
成1200的角,则k= .
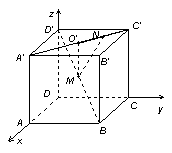 三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)如图,已知正方体![]() 的棱长为a,M为
的棱长为a,M为![]() 的中点,点N在
的中点,点N在![]() '上,且
'上,且![]() ,试求MN的长.
,试求MN的长.
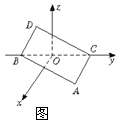
16.(12分)如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(![]() ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
 (1)求向量
(1)求向量![]() 的坐标;
的坐标;
(2)设向量![]() 和
和![]() 的夹角为θ,求cosθ的值
的夹角为θ,求cosθ的值
17.(12分)若四面体对应棱的中点间的距离都相等,证明这个四面体的对棱两两垂直.
18.(12分)四棱锥P—ABCD中,底面ABCD是一个平行四边形,![]() ={2,-1,-4},
={2,-1,-4},![]() ={4,2,0},
={4,2,0},![]() ={-1,2,-1}.
={-1,2,-1}.
(1)求证:PA⊥底面ABCD;
(2)求四棱锥P—ABCD的体积;
(3)对于向量![]() ={x1,y1,z1},
={x1,y1,z1},![]() ={x2,y2,z2},
={x2,y2,z2},![]() ={x3,y3,z3},定义一种运算:
={x3,y3,z3},定义一种运算:
(![]() ×
×![]() )·
)·![]() =x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算(
=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算(![]() ×
×![]() )·
)·![]() 的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(
的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(![]() ×
×![]() )·
)·![]() 的绝对值的几何意义..
的绝对值的几何意义..
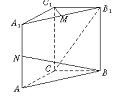
19.(14分)如图所示,直三棱柱ABC—A1B
(1)求![]() 的长;
的长;
(2)求cos<![]() >的值;
>的值;
(3)求证:A1B⊥C1M.
20.(14分)如图,已知平行六面体ABCD—A1B
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=![]() ,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
(3)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
参考答案
一、1.A;解析:![]() =
=![]() +
+![]() (-
(-![]() )=-
)=-![]()
![]() +
+![]()
![]() +
+![]() .评述:用向量的方法处理立体几何问题,使复杂的线面空间关系代数化,本题考查的是基本的向量相等,与向量的加法.考查学生的空间想象能力.
.评述:用向量的方法处理立体几何问题,使复杂的线面空间关系代数化,本题考查的是基本的向量相等,与向量的加法.考查学生的空间想象能力.
2.A;解析:空间的四点P、A、B、C共面只需满足![]() 且
且![]() 既可.只有选项A.
既可.只有选项A.
3.B;解析:只需将![]() ,运用向量的内即运算即可,
,运用向量的内即运算即可,![]() .
.
4.C;解析:向量的共线和平行使一样的,可利用空间向量共线定理写成数乘的形式.即![]() .
.
5.C;解析: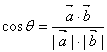 ,计算结果为-1.
,计算结果为-1.
6.B;解析:显然![]() .
.
7.B;解析:过点A的棱两两垂直,通过设棱长应用余弦定理可得三角形为锐角三角形.
8.D;解析:建立一组基向量![]() ,再来处理
,再来处理![]() 的值.
的值.
9.D;解析:应用向量的运算,显然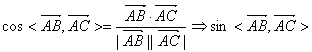 ,从而得
,从而得![]() .
.
10.C;
二、
11.![]() ;解析:
;解析: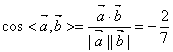 ,得
,得![]() ,可得结果.
,可得结果.
12.
![]() ;
;
解析:
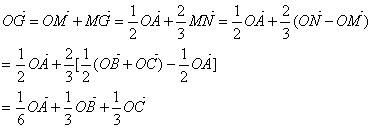
13.直角三角形;解析:利用两点间距离公式得:![]() .
.
14.![]() ;解析:
;解析: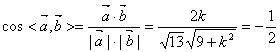 ,得
,得![]() .
.
三、
15.解:以D为原点,建立如图空间直角坐标系.因为正方体棱长为a,所以B(a,a,0),A'(a,0,a),![]() (0,a,a),
(0,a,a),![]() (0,0,a).
(0,0,a).
由于M为![]() 的中点,取
的中点,取![]() 中点O',所以M(
中点O',所以M(![]() ,
,![]() ,
,![]() ),O'(
),O'(![]() ,
,![]() ,a).因为
,a).因为![]() ,所以N为
,所以N为![]() 的四等分,从而N为
的四等分,从而N为![]() 的中点,故N(
的中点,故N(![]() ,
,![]() ,a).
,a).
根据空间两点距离公式,可得
![]() .
.
16.解:(1)过D作DE⊥BC,垂足为E,在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,得BD=1,CD=![]() ,∴DE=CD·sin30°=
,∴DE=CD·sin30°=![]() .
.
OE=OB-BE=OB-BD·cos60°=1-![]() .
.
∴D点坐标为(0,-![]() ),即向量OD[TX→]的坐标为{0,-
),即向量OD[TX→]的坐标为{0,-![]() }.
}.
(2)依题意:![]() ,
,
所以![]() .
.
设向量![]() 和
和![]() 的夹角为θ,则
的夹角为θ,则
cosθ=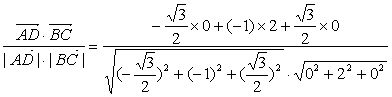
![]() .
.
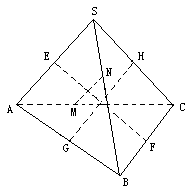 17. 证:如图设
17. 证:如图设![]() ,则
,则![]() 分别为
分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由条件EH=GH=MN得:
,由条件EH=GH=MN得:
![]()
展开得![]()
∴![]() ,∵
,∵![]() ≠
≠![]() ,
,![]() ≠
≠![]() ,
,
∴![]() ⊥(
⊥(![]() )即SA⊥BC.
)即SA⊥BC.
同理可证SB⊥AC,SC⊥AB.
18. (1)证明:∵![]() =-2-2+4=0,∴AP⊥AB.
=-2-2+4=0,∴AP⊥AB.
又∵![]() =-4+4+0=0,∴AP⊥AD.
=-4+4+0=0,∴AP⊥AD.
∵AB、AD是底面ABCD上的两条相交直线,∴AP⊥底面ABCD.
(2)解:设![]() 与
与![]() 的夹角为θ,则
的夹角为θ,则
cosθ=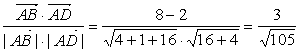
V=![]()
![]() ·
·![]() ·sinθ·
·sinθ·![]() =
=![]()
(3)解:(![]() ×
×![]() )·
)·![]() =-4-32-4-8=48它是四棱锥P—ABCD体积的3倍.
=-4-32-4-8=48它是四棱锥P—ABCD体积的3倍.
猜测:(![]() ×
×![]() )·
)·![]() 在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).
在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).
评述:本题考查了空间向量的坐标表示、空间向量的数量积、空间向量垂直的充要条件、空间向量的夹角公式和直线与平面垂直的判定定理、棱锥的体积公式等.主要考查考生的运算能力,综合运用所学知识解决问题的能力及空间想象能力.
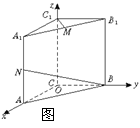 19.如图,建立空间直角坐标系O—xyz.
19.如图,建立空间直角坐标系O—xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴![]() =
=![]() .
.
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴![]() ={-1,-1,2},
={-1,-1,2},![]() ={0,1,2,},
={0,1,2,},![]() ·
·![]() =3,
=3,![]() =
=![]() ,
,![]() =
=![]()
∴cos<![]() ,
,![]() >=
>=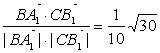 .
.
(3)证明:依题意,得C1(0,0,2)、M(![]() ,2),
,2),![]() ={-1,1,2},
={-1,1,2},![]() ={
={![]() ,0}.∴
,0}.∴![]() ·
·![]() =-
=-![]() +0=0,∴
+0=0,∴![]() ⊥
⊥![]() ,∴A1B⊥C1M.
,∴A1B⊥C1M.
评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件.
20.(1)证明:设![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,则
,则![]() =
=![]() ,∵
,∵![]() =
=![]() -
-![]() ,
,
∴![]() ·
·![]() =(
=(![]() -
-![]() )·
)·![]() =
=![]() ·
·![]() -
-![]() ·
·![]() =
=![]() ·
·![]() cos60°-
cos60°-![]() ·
·![]() cos60°=0,
cos60°=0,
∴C1C⊥BD.
(2)解:连AC、BD,设AC∩BD=O,连OC1,则∠C1OC为二面角α—BD—β的平面角.
∵![]() (
(![]() +
+![]() ),
),![]() (
(![]() +
+![]() )-
)-![]()
∴![]() ·
·![]() (
(![]() +
+![]() )·[
)·[![]() (
(![]() +
+![]() )-
)-![]() ]
]
=![]() (
(![]() 2+2
2+2![]() ·
·![]() +
+![]() 2)-
2)-![]()
![]() ·
·![]() -
-![]()
![]() ·
·![]()
=![]() (4+2·2·2cos60°+4)-
(4+2·2·2cos60°+4)-![]() ·2·
·2·![]() cos60°-
cos60°-![]() ·2·
·2·![]() cos60°=
cos60°=![]() .
.
则![]() =
=![]() ,
,![]() =
=![]() ,∴cosC1OC=
,∴cosC1OC=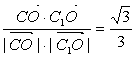
(3)解:设![]() =x,CD=2,
则CC1=
=x,CD=2,
则CC1=![]() .
.
∵BD⊥平面AA1C1C,∴BD⊥A1C
∴只须求满足:![]() =0即可.
=0即可.
设![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,
∵![]() =
=![]() +
+![]() +
+![]() ,
,![]() =
=![]() -
-![]() ,
,
∴![]() =(
=(![]() +
+![]() +
+![]() )(
)(![]() -
-![]() )=
)=![]() 2+
2+![]() ·
·![]() -
-![]() ·
·![]() -
-![]() 2=
2=![]() -6,
-6,
令6-![]() =0,得x=1或x=-
=0,得x=1或x=-![]() (舍去).
(舍去).
评述:本题蕴涵着转化思想,即用向量这个工具来研究空间垂直关系的判定、二面角的求解以及待定值的探求等问题.