新课标高二数学同步测试(6)—(2-2第一章1.1—1.4)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.两曲线![]() 相切于点(1,-1)处,则a,b值分别为( )
相切于点(1,-1)处,则a,b值分别为( )
A.0,2 B.1,-
2.![]() ( )
( )
A.在(-∞,+∞)单调增加
B.在(-∞,+∞)单调减少
C.在(-1,1)单调减少,其余区间单调增加
D.在(-1,1)单调增加,其余区间单调减少
3.当x≠0时,有不等式 ( )
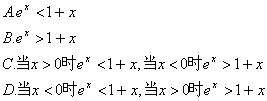
4.若连续函数在闭区间上有惟一的极大值和极小值,则 ( )
A.极大值一定是最大值,极小值一定是最小值
B.极大值必大于极小值
C.极大值一定是最大值,或极小值一定是最小值
D.极大值不一定是最大值,极小值也不一定是最小值
5.![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D
.
D
.![]()
6.下列求导运算正确的是 ( )
A.(x+![]() B.(log2x)′=
B.(log2x)′=![]()
C.(3x)′=3xlog3e D.(x2cosx)′=-2xsinx
7.函数f(x)= a x2+x+1有极值的充要条件是 ( )
A.a >0 B.a≥0
C.a <0 D.a ≤0
8.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,![]() >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
|
A.若a<0,则函数g(![]() )的图象关于原点对称.
)的图象关于原点对称.
B.若a=-1,-2<b<0,则方程g(![]() )=0有大于2的实根.
)=0有大于2的实根.
C.若a≠0,b=2,则方程g(![]() )=0有两个实根.
)=0有两个实根.
D.若a≥1,b<2,则方程g(![]() )=0有三个实根
)=0有三个实根
10.已知函数f (x)的导数为![]() 且图象过点(0,-5),当函数f (x)取得极大值-5时,x的值应为 ( )
且图象过点(0,-5),当函数f (x)取得极大值-5时,x的值应为 ( )
A.-1 B.0
C.1 D.±1
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.函数f(x)=x+2cosx在区间![]() 上的最大值为_________;在区间[0,2π]上最大值为___________.
上的最大值为_________;在区间[0,2π]上最大值为___________.
12.已知![]() ,奇函数
,奇函数![]() 在
在![]() 上单调,则字母
上单调,则字母![]() 应满足的条件是 .
应满足的条件是 .
13.两个和为48的正整数,第一个数的立方与第二个数的平方之和最小,则这两个正整数分别为__________.
14.![]()
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
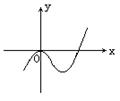 15.(12分)设函数y=x3+ax2+bx+c的图象如图所示,且与y=0在原点相切,若函数的极小值为-4,(1)求a、b、c的值;(2)求函数的递减区间.
15.(12分)设函数y=x3+ax2+bx+c的图象如图所示,且与y=0在原点相切,若函数的极小值为-4,(1)求a、b、c的值;(2)求函数的递减区间.
16.(12分)是否存在这样的k值,使函数![]() 在(1,2)上递减,在(2,-∞)上递增.
在(1,2)上递减,在(2,-∞)上递增.
17.(12分)设函数![]()
(1)求导数![]() ; 并证明
; 并证明![]() 有两个不同的极值点
有两个不同的极值点![]() ;
;
(2)若不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
18.(12分)讨论函数![]() 的单调性,并确定它在该区间上的最大值最小值.
的单调性,并确定它在该区间上的最大值最小值.
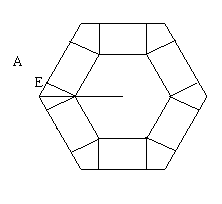
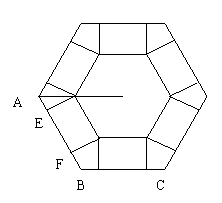
19.(14分)如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为h所做成的盒子体积V(不计接缝).
(1)写出体积V与高h的函数关系式;
 (2)当
(2)当![]() 为多少时,体积V最大,最大值是多少?
为多少时,体积V最大,最大值是多少?
20.(14分)已知过函数f(x)=![]() 的图象上一点B(1,b)的切线的斜率为-3.
的图象上一点B(1,b)的切线的斜率为-3.
(1)求a、b的值;
(2)求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立;
令![]() .是否存在一个实数t,使得当
.是否存在一个实数t,使得当![]() 时,g(x)有最大值1?
时,g(x)有最大值1?
参考答案
一、
1.D;2.C;3.B;4.D;
5.D 提示:这里插入![]() ,因为题目假定f(x)在
,因为题目假定f(x)在![]() 点可导,所以分成两项的极限都存在.
点可导,所以分成两项的极限都存在.
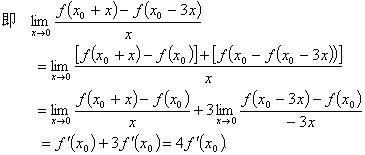
![]()
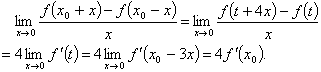
因为题中只设f(x)在![]() 可导,没说在
可导,没说在![]() 及其邻域内可导,更没假定
及其邻域内可导,更没假定![]() 在
在![]() 点连续,所以上面的做法是无根据的.
点连续,所以上面的做法是无根据的.
6.D;7.C 8.D 9.B 10.B
二、
11.![]() ;提示:
;提示:![]() 得f(x)的驻点为
得f(x)的驻点为![]() ,当在区间
,当在区间![]() 内考虑时,仅有一个驻点
内考虑时,仅有一个驻点![]() 比较后得知,f(x)在
比较后得知,f(x)在![]() 上的最大值为
上的最大值为![]() ,而当考虑区间[0,2π]上的最大值时,需比较f(0),
,而当考虑区间[0,2π]上的最大值时,需比较f(0),
f(2π),![]() 四个值的大小.
四个值的大小.
12.![]() ;解析:
;解析:![]() ;
;![]() .
.
![]() ,
,
若![]()
![]() 上是增函数,则
上是增函数,则![]() 恒成立,即
恒成立,即![]() ;
;
若![]()
![]() 上是减函数,则
上是减函数,则![]() 恒成立,这样的
恒成立,这样的![]() 不存在.;
不存在.;
综上可得:![]()
13.5与43;
14.1000!;提示:![]()
三、
15.解析:(1)函数的图象经过(0,0)点
∴
c=0,又图象与x轴相切于(0,0)点,![]() =3x2+2ax+b
=3x2+2ax+b
∴ 0=3×02+2a×0+b,得b=0
∴ y=x3+ax2,![]() =3x2+2ax
=3x2+2ax
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
当x=![]() 时,函数有极小值-4
时,函数有极小值-4
∴ ![]() ,得a=-3
,得a=-3
(2)![]() =3x2-6x<0,解得0<x<2
=3x2-6x<0,解得0<x<2
∴ 递减区间是(0,2)
点拨:1、如果函数f(x)在点x=x0的一个δ区域:(x0-δ,x0+δ)内有定义,对任意的x∈(x0-δ,x0)∪(x0,x0+δ)总有f(x)<f(x0)(f(x)>f(x0)),则称f(x0)为函数f(x)的极大(小)值,x0称为极大(小)值点;
2、注意极值与最值的区别,极值是相对于领域而言,它仅是极值点附近的局部范围内的相对大小,而最值是相对于闭区间而言,它是函数在给定的闭区间上的全部函数值中最大(小)的值.
16.解析:f(x)=4k2x3-2x2-2kx+2,由题意,当x∈(1,2)时,![]() <0
<0
当x∈(2,+∞)时,![]() >0
>0
由函数![]() 的连续性可知
的连续性可知![]() =0
=0
即32k2-8-3=0得![]() 或
或![]()
验证:当![]() 时,
时,![]()
若1<x<2,![]() ,
,
若x>2,![]() ,符合题意
,符合题意
当![]() 时,
时,![]()
显然不合题意
综上所述,存在![]() ,满足题意
,满足题意
点拨:利用导数处理单调性问题,讨论的区间是开区间,注意递增与递减区间的交界处的导数为0,本题求出k值后还需讨论验证.
17.(1)![]()

因此![]() 是极大值点,
是极大值点,![]() 是极小值点.
是极小值点.
(II)因![]()
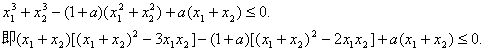
又由(I)知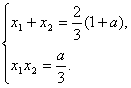
代入前面不等式,两边除以(1+a),并化简得
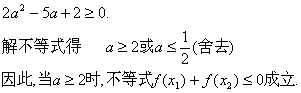
18.解:设![]() 则
则![]() ,于是当0<x≤2时,
,于是当0<x≤2时,![]() 而只有x=0时,
而只有x=0时,![]() ,故在[0,2]上
,故在[0,2]上![]() 为单调减少,
为单调减少,
而![]() 所以
所以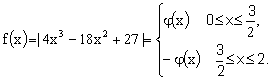 在
在![]() 为单调减少,在
为单调减少,在![]() 为单调增加,
为单调增加,
因而在[0,2]上f(x)的最大值f(0)=27,最小值![]()
 19.解:(1)六棱柱的底边长(
19.解:(1)六棱柱的底边长(![]() )cm,
)cm,
底面积为(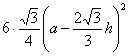 )cm2
)cm2
∴体积V=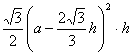
=![]()
(2)V′=![]() 得
得![]() 或
或![]() (舍去)
(舍去)
∴当![]() cm时V有最大值
cm时V有最大值![]() cm3
cm3
20.解:(1)![]() =
=![]()
依题意得k=![]() =3+2a=-3,
∴a=-3
=3+2a=-3,
∴a=-3
![]() ,把B(1,b)代入得b=
,把B(1,b)代入得b=![]()
∴a=-3,b=-1
(2)令![]() =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004.
(1)
已知g(x)=-![]()
∴![]()
∵0<x≤1,∴-3≤-3x2<0,
①
当t>3时,t-3x2>0,![]()
∴g(x)在![]() 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
②
当0≤t≤3时, ![]()
令![]() =0,得x=
=0,得x=![]()
列表如下:
| x | (0, |
|
|
|
| + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
g(x)在x=![]() 处取最大值-
处取最大值-![]() +t
+t![]() =1
=1
∴t=![]() =
=![]() <
<![]() 3
3
∴x=![]() <1
<1
③当t<0时,![]() <0,∴g(x)在
<0,∴g(x)在![]() 上为减函数,
上为减函数,
∴g(x)在![]() 上为增函数,
上为增函数,
∴存在一个a=![]() ,使g(x)在
,使g(x)在![]() 上有最大值1.
上有最大值1.