高二上期末考试模拟试题十六
数 学
(测试时间:120分钟 满分150分)
一.选择题
1.抛物线![]() 的准线方程是(
)
的准线方程是(
)
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
2.焦点在直线![]() 上的抛物线的标准方程是(
)
上的抛物线的标准方程是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.抛物线的顶点在原点O,焦点在![]() 轴的正半轴上,过焦点且垂直于
轴的正半轴上,过焦点且垂直于![]() 轴的弦AB与顶点O所成的
轴的弦AB与顶点O所成的![]() 面积是4,则抛物线的方程为( )
面积是4,则抛物线的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.抛物线![]() 的准线与椭圆
的准线与椭圆![]() 的左准线重合,则抛物线的焦点坐标是( )
的左准线重合,则抛物线的焦点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若双曲线![]() 的一条准线与抛物线
的一条准线与抛物线![]() 的准线重合,则双曲线的离心率为( )
的准线重合,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
6.过点![]() 与抛物线
与抛物线![]() 只有一个公共点的直线有( )
只有一个公共点的直线有( )
A.1条 B.2条 C.3条 D.4条
7.焦点为![]() ,准线方程是
,准线方程是![]() 的抛物线方程是( )
的抛物线方程是( )
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
8.试在抛物线![]() 上求一点P,使其到焦点F的距离与到
上求一点P,使其到焦点F的距离与到![]() 的距离之和最小,则该点坐标为( )
的距离之和最小,则该点坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.抛物线![]() 截直线
截直线![]() 所得弦长等于( )
所得弦长等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.过抛物线![]() 的焦点作一条直线交抛物线于
的焦点作一条直线交抛物线于![]() ,则
,则![]() 等于( )
等于( )
A.4
B.-![]() D.
D.![]()
11.过抛物线![]() 的焦点作一直线交直线于P.Q两点,若线段PF与FQ的长分别时
的焦点作一直线交直线于P.Q两点,若线段PF与FQ的长分别时![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设抛物线![]() 的准线与
的准线与![]() 轴交于点Q,若过点Q的直线
轴交于点Q,若过点Q的直线![]() 与抛物线有公共点,则直线
与抛物线有公共点,则直线![]() 的斜率的取值范围是( )
的斜率的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题
13.抛物线![]() 的焦点到准线的距离为
.
的焦点到准线的距离为
.
14.过点![]() 和抛物线
和抛物线![]() 仅有一个交点的直线方程是
.
仅有一个交点的直线方程是
.
15.过抛物线![]() 内一点
内一点![]() 作弦BC,若A为BC的中点,则直线BC的方程为 ,其中m的取值范围是
.
作弦BC,若A为BC的中点,则直线BC的方程为 ,其中m的取值范围是
.
16.抛物线![]() 上的点到直线
上的点到直线![]() 的最近距离为 ,此点坐标为
.
的最近距离为 ,此点坐标为
.
三.解答题
17.一抛物线的定点A,焦点F分别是双曲线![]() 的右焦点和左顶点,求此抛物线的方程.
的右焦点和左顶点,求此抛物线的方程.
18.抛物线的焦点F在![]() 轴上,直线
轴上,直线![]() 与抛物线相交于A,
与抛物线相交于A,![]() 求抛物线的标准方程.
求抛物线的标准方程.
19.OA,OB是抛物线![]() 的两条互相垂直的弦,O为原点,求弦AB中点的轨迹方程.
的两条互相垂直的弦,O为原点,求弦AB中点的轨迹方程.
20.过抛物线![]() 的顶点作两条垂直的弦OA,OB,
的顶点作两条垂直的弦OA,OB,
(1)求证直线AB恒过一定点;(2)求AB中点的轨迹.
21.直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,P是线段
两点,P是线段![]() 的中点,直线
的中点,直线![]() 过P和抛物线的焦点F,设直线
过P和抛物线的焦点F,设直线![]() 的斜率为
的斜率为![]() (1)将直线
(1)将直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之比表示为
的斜率之比表示为![]() 的函数
的函数![]() ;(2)求出
;(2)求出![]() 的定于域及单调区间.
的定于域及单调区间.
22.已知抛物线:![]()
(1)若![]() ,设
,设![]() ,求抛物线上距点A最近的点B的坐标及相应的距离
,求抛物线上距点A最近的点B的坐标及相应的距离![]() ;
;
(2) 若![]() ,设
,设![]() ,
,![]() ,抛物线上的点B到点A的最小距离
,抛物线上的点B到点A的最小距离![]() ,并求
,并求![]() 时点A的坐标;
时点A的坐标;
(3)若![]() 到抛物线上的点的最小距离为4,求抛物线的方程.
到抛物线上的点的最小距离为4,求抛物线的方程.
参考答案
一.选择题
1—5.DDBCA 6—10 CDAAB 11—12 BC
二.填空题
13. 5 14.![]() 15.
15.![]()
16.![]() ,
,![]()
17.解:![]() 双曲线
双曲线![]() 的右焦点坐标为
的右焦点坐标为![]() ,
,
左顶点坐标为![]()
![]() 抛物线的顶点A
抛物线的顶点A![]() ,焦点F
,焦点F![]()
![]() .
.
18.解:设所求焦点在![]() 轴上的抛物线标准方程为:
轴上的抛物线标准方程为:![]() 则由抛物线的定义得
则由抛物线的定义得![]() 又
又![]()
![]() 故所求抛物线方程为
故所求抛物线方程为![]()
19.解:设![]() ,AB的中点坐标为
,AB的中点坐标为![]()
![]()
![]()
![]()
又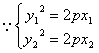
![]()
![]()
又![]()
![]()
![]()
又![]() 的中点
的中点
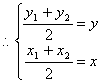
![]()
![]()
20.解:(1)设![]()
![]() ,B是抛物线
,B是抛物线![]() 上的点
上的点
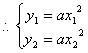
![]()
![]()
![]()
![]()
又![]() ①
①
![]()
![]()
![]()
![]()
![]() 代入①得
代入①得
![]()
![]()
![]() .
.
(2)设AB的中点![]()
![]()
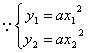
![]()
![]()
![]()
又![]()
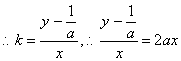
![]() .
.
21.解:(1)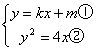
将①代入②得
![]()
![]()
由①得![]() 代入②得
代入②得![]()
![]()
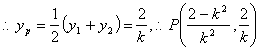
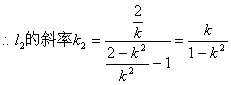
![]()
(2)![]()
![]()
![]()
① 当![]()
② 当![]()
证明:当![]()
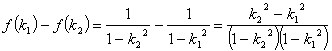
![]()
![]()
![]()
![]() .
.
同理![]() .
.
22.解:设![]()
![]()
①当![]() 时,
时,![]()
![]() ,
,![]()
②![]()
![]()
当对称轴![]()
当对称轴![]()
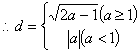
![]()
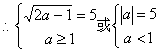
![]()
③![]()
若对称轴![]()
![]() 不合题意,舍去.
不合题意,舍去.
若对称轴![]()
![]()
![]()
![]() .
.
|