高二数学上期末考试模拟试题17

高二上期末考试模拟试题十七

数　　　　学

（测试时间：120分钟　　满分150分）

一．选择题

1. 中心在原点，对称轴为坐标轴，离心率，一条准线方程为的双曲线方程是（　 ）

（A）　 （B）　（C）　　 （D）

2．已知、，，当和时，的轨迹分别是（　）

（A）双曲线和一条直线　　　　 （B）双曲线和两条射线　

（C）双曲线的一支和一条直线　 （D）双曲线的一支和一条射线

3．若方程表示双曲线，则的取值范围是（　）

（A）　　　　　  （B）或　

（C）且　　　　（D）

4．（2005福建高考）已知、是双曲线的两焦点，以线段为边作正三角形，若边的中点在双曲线上，则双曲线的离心率是（　）

（A）　 （B）　 （C）　 （D）

5．设P是双曲线上一点，双曲线的一条渐近线方程为、F₂分别是双曲线的左、右焦点，若，则（　　）

  A. 1或5　　 　B. 6　　 　C. 7　　 D. 9

6．与曲线共焦点，而与曲线共渐近线的双曲线方程为（　 ）

　　　 A． B． C． D．

7．若椭圆与双曲线有相同的焦点F₁、F₂，P是两曲线的一个交点，则的面积是（　　）

　　 A．4　　B．2　　C．1　　D．　　　　　　　　　

8．以坐标轴为对称轴，以为渐近线且过点的双曲线的准线方程是（　 ）

（A）　 （B）　 （C）　（D）

9．（湖南卷）已知双曲线－＝1（a＞0，b＞0）的右焦点为F，右准线与一条渐近线交于点A，△OAF的面积为（O为原点），则两条渐近线的夹角为（　）　　　　　　　　　　　　　　　　　　　　　　　　　

　　A．30º　　　　　　　　　B．45º　　　　　　　　　 C．60º　　　　　　　　　D．90º

10．(全国卷II)已知双曲线的焦点为、，点在双曲线上且轴，则到直线的距离为(C )

(A) 　　　　　　　　　 (B) 　　　　　　　　　 (C) 　　　　　　　　　　　 (D)

11．已知双曲线，若将该双曲线绕着它的右焦点逆时针旋转后，所得双曲线的一条准线方程是（　　 ）

（A）　　　　（B）　　  （C）　　  （D）

12．直线与实轴在轴上的双曲线的交点在以原点为中心、边长为且各边分别平行于坐标轴的正方形的内部，则的取值范围是（　　）

（A）　　（B）　　（C）　　　（D）

二．填空题

13．已知是双曲线的两焦点，过点的直线交双曲线于点，若则等于　　　　　　　　　　

14．若曲线的焦点为定点，则焦点坐标是　　　　　　　 

15．设椭圆和双曲线的公共焦点为是两曲线的一个公共点，则等于　　　　　　　

16．直线与双曲线相交于两点，若以的直径的圆过原点，则的值为 　　　　　　　　　　　　　；　

三．解答题

17．已知双曲线的中心在原点，焦点、在轴上，离心率，且过点（1）求此双曲线方程

（2）若圆过此双曲线的一个顶点和一个焦点，且圆心在此双曲线上，求圆心到双曲线中心的距离.

18．已知双曲线方程为，过左焦点作倾斜角为的直线交双曲线于A、B两点

（1）求弦AB的长

（2）求左焦点F₁到AB中点M的长。

19．给定双曲线，是否存在被点平分的弦？若存在，求出弦所在的直线方程；若不存在，请说明理由。

20．设双曲线与直线相交于两个不同的点.

（1）求双曲线的离心率的取值范围.

（2）设直线与轴的交点为，且，求的值.

21．A、B、C是我军三个炮兵阵地，A在B的正东方向相距6千米，C在B的北30°西方向,相距4千米,P为敌炮阵地.某时刻,A发现敌炮阵地的某信号,由于B、C比A距P更远，因此，4秒后，B、C才同时发现这一信号（该信号的传播速度为每秒1千米）.若从A炮击敌阵地P，求炮击的方位角.　　　

22．(2005重庆卷) 已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为。

　　(1) 求双曲线C的方程；

　　(2) 若直线l：与双曲线C恒有两个不同的交点A和B，且(其中O为原点)，求k的取值范围。

参考答案

一、选择题

CDADC　ACCDC　AC

二、填空题

13．21　　　 14．　　15．　　 16．

三、解答题

17．解：（1），  .　

可设双曲线方程为

　点在双曲线上，

因此双曲线方程是.

(2)显然,焦点与顶点是相对同一支的焦点和顶点,设为，，

则圆心在直线上，代入双曲线方程得

 圆心到双曲线中心的距离为

18．解： a=3,b=1,c=,：y=(x＋)即x=y－.

将其代入x²－9y²－9=0.得6y²+2y－1=0,y₁＋y₂=－,∴－.

∴AB

F₁M==×=.

19．解：假设存在这样的弦，设、，则

由题意由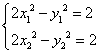　　　　　　　　　　 

（1）　　　 －（2）得

于是弦所在的直线方程为，即，将其代入双曲线方程，整理得　

，说明此时直线与双曲线无公共点，矛盾

故不存在这样的弦。翰林汇

20．解：（I）由C与相交于两个不同的点，故知方程组

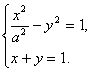
有两个不同的实数解.消去y并整理得 （1－a²）x²+2a²x－2a²=0.　　 ①

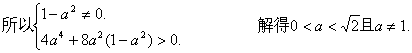
双曲线的离心率

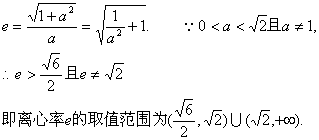
（II）设

由于x₁，x₂都是方程①的根，且1－a²≠0，

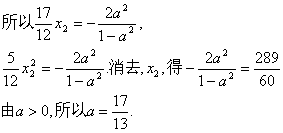
21．解.以线段AB的中点为原点，正东方向为轴的正方向建立直角坐标系，则 依题意　　　　在以A、B为焦点的双曲线的右支上.这里.其方程为  

又 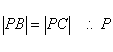 又在线段AB的垂直平分线上

由方程组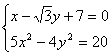  解得　 　即  

由于，可知P在北30°东方向.

22. 解：（Ⅰ）设双曲线方程为　

由已知得

故双曲线C的方程为

（Ⅱ将

由直线l与双曲线交于不同的两点得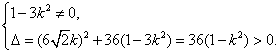

即　①　设，则

而

于是　　②

由①、②得　

故k的取值范围为

O