高二上期末考试模拟试题十八
数 学
（测试时间：120分钟 满分150分）
一、 选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中有只有一项是符合题目要求的.）
1．椭圆
的焦距是 （ ）
A．2 B．
C．
D．
2．F1、F2是定点，F1F2=6，动点M满足MF1+MF2=6，则点M的轨迹是 （ ）
A．椭圆 B．直线 C．线段 D．圆
3．若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点
，则椭圆方程是 （ ）
A．
B．
C．
D．
4．方程
表示焦点在y轴上的椭圆，则k的取值范围是 （ ）
A．
B．（0，2） C．（1，+∞） D．（0，1）
5. 过椭圆
的一个焦点
的直线与椭圆交于
、
两点，则、与椭圆的另一焦点
构成
，那么的周长是（ ）
A. 
B.
2
C. 
D.
1
6．若椭圆两准线间的距离等于焦距的4倍，则这个椭圆的离心率为 （ ）
A．
B．
C．
D． 
7. 已知
＜4，则曲线
和
有（ ）
A. 相同的准线 B. 相同的焦点 C. 相同的离心率 D. 相同的长轴
8．已知
是椭圆
上的一点，若到椭圆右准线的距离是
，则点到左焦点的距离是 （ ）
A．
B．
C．
D．
9．若点在椭圆
上，、分别是椭圆的两焦点，且
，则
的面积是（ ）
A. 2
B. 1
C. 
D.
10．椭圆
内有一点P（3，2）过点P的弦恰好以P为中点，那么这弦所在直线的方程为 （ ）
A．
B．
C．
D． 
11．椭圆
上的点到直线
的最大距离是 （ ）
A．3 B．
C．
D．
12．在椭圆
内有一点P（1，－1），F为椭圆右焦点，在椭圆上有一点M，使MP+2MF的值最小，则这一最小值是 （ ）
A．
B．
C．3 D．4
二、 填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上.）
13．椭圆
的离心率为
，则
。
14．设是椭圆
上的一点，
是椭圆的两个焦点，则
的最大值为 ；最小值为
。
15．直线y=x－
被椭圆x2+4y2=4截得的弦长为
。
16．已知圆
为圆上一点，AQ的垂直平分线交CQ于M，则点M的轨迹方程为
。
三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.）
17．已知三角形
的两顶点为
，它的周长为
,求顶点轨迹方程．
18、椭圆的一个顶点为A（2，0），其长轴长是短轴长的2倍，求椭圆的标准方程．
19、中心在原点，一焦点为F1（0，5
）的椭圆被直线y=3x－2截得的弦的中点横坐标是，求此椭圆的方程。
20、设椭圆的中心是坐标原点，长轴在x轴上，离心率e=
，已知点P（0，
）到椭圆上的点的最远距离是
，求这个椭圆方程。
21、椭圆
上不同三点
与焦点
F（4，0）的距离成等差数列．
（1）求证 
；
（2）若线段 
的垂直平分线与
轴的交点为
，求直线
的斜率
．
22、椭圆
＞
＞
与直线
交于、
两点，且
，其中
为坐标原点.
（1）求
的值；
（2）若椭圆的离心率
满足
≤≤
，求椭圆长轴的取值范围.
单元练习(七)参考答案
一、选择题：
ACDD ADBD BBDC
二、填空题
13、3或
14、 4 ， 1
15、
16、
三、 解答题
17、
18、解：（1）当 
为长轴端点时，
，
，
椭圆的标准方程为： 
；
（2）当 为短轴端点时，
，
，
椭圆的标准方程为： 
；
19、设椭圆：
（a＞b＞0），则a2＋b2=50…①
又设A（x1，y1），B（x2，y2），弦AB中点（x0，y0）
∵x0=，∴y0=－2=－
由
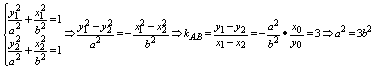…②
解①，②得：a2=75，b2=25，椭圆为：
=1
20、 ∵e2==
∴椭圆方程可设为：
设A（x，y）是椭圆上任一点，则：│PA│2=x2+（y－）2=－3y2－3y+4b2+
f（y）（－b≤y≤b）
讨论：1°、－b＞－
0＜b＜时，│PA│
= f（－b）=（b＋）2
=
但b＞，矛盾。不合条件。
2°、－b≤－ b≥时，│PA│= f（－）=4b2+3=7 b2=1
∴所求椭圆为：
21、证明：（1）由椭圆方程知 
，
，
．
由圆锥曲线的统一定义知：
，
∴ 
．
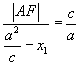同理 
．
∵ 
，且 
，
∴ 
，
即 ．
（2）因为线段 的中点为
，所以它的垂直平分线方程为
又∵点 在
轴上，设其坐标为
，代入上式，得
又∵点 
，
都在椭圆上，
∴ 
∴ 
．
将此式代入①，并利用 的结论得
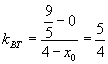
22、[解析]：设
，由OP ⊥ OQ 
x 1 x 2
+ y 1 y 2 = 0
又将
，
代入①化简得 
.
(2) 
又由（1）知
，∴长轴 2a ∈ [
].
|