高二上期末考试模拟试题十九
数 学
（测试时间：120分钟 满分150分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1．如果曲线C上的点满足方程
，则以下说法正确的是（ ）
A．曲线C的方程是
B. 坐标满足方程的点在曲线C上
C. 方程的曲线是C D．坐标不满足方程的点不在曲线C上
2.方程
所表示的曲线是（ ）
A. 关于
轴对称
B. 关于直线
对称
C. 关于原点对称
D. 关于直线
对称
3．已知点A（-3，0），B（0，
），C（4，
），D（
, 
）,其中在曲线
上的点的个数为（ ）
A.1 B.2 C.3 D.4
4．设圆的参数方程是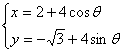
（
为参数），则圆上一点
对应的参数等于（ ）
A. 
B.
C. 
D. 
5．方程
的曲线的周长及其所围成的区域的面积分别为( )
A.
，1 B. 
，2 C. 
，4 D.8，4
6．若方程
表示一个圆，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
或
7．两圆
和
的公切线有（ ）
A. 1条 B. 2条 C. 3条 D. 4条
8.直线
截圆
得的劣弧所对的圆心角为（ ）
A. 
B.
C.
D.
9.过点
且与已知圆
切于点
的圆的方程是（ ）
A. 
B.
C. 
D.
10.如果实数
、满足
，那么
的最小值是（ ）
A. 
B.
C.
D.
11.“
＞1”是“曲线
与直线
有且仅有两个交点”的（ ）
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
12．以（-4，3）为圆心的圆与直线
相离，则其半径r的取值范围是( )
A.0＜r＜2
Ｂ.0＜r＜
Ｃ.0＜r＜2
Ｄ.0＜r＜10
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.
13.若点
在曲线
上，则
的最大值是_ _。
14.两圆
和
的公共弦所在的直线方程为 。
15.已知直线
与圆
有两个公共点
、
，且轴正半轴沿逆时针转到两射线
、
（
为坐标原点）的最小正角依次为
、
，则
= 。
16.已知点A(1，2),B(-4，4)，而点C在圆(x-3)2+(y+6)2=9上运动，则△ABC的重心的轨迹方程为_________。
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
自点
发出的光线
射到轴上，被轴反射，其反射光线
所在直线与圆C：
相切，求入射光线所在直线的方程。
18．（本小题满分12分）
已知曲线
和
，当为何值时，两曲线有且只有一个交点。
19．（本小题满分12分）
求过直线
和圆
的交点，且面积最小的圆的方程。
20．（本小题满分12分）
曲线
上两点P、Q，满足：
（1） 关于直线
对称；
（2） OP⊥OQ。
求直线PQ的方程。
21．（本小题满分12分）
过一个定点
任作互相垂直的两条直线
和
，且与轴相交于点，与轴相交于点，求线段中点
的轨迹方程，并说明是怎样的轨迹。
22．（本小题满分14分）
已知点
是圆
上的动点，
(1)若
，求
的取值范围；
(2)若
恒成立，求实数的取值范围。
单元练习(六)参考答案
1——5：DCCDB；6——10：DCCAD；11——12：AC
13、
14、
15、
16、
17、解：依题意知：反射光线m过点
，
设直线m的方程为y+3=k（x+3），即
由得：
，直线m与圆相切，
，解得：
或
故直线m的方程为
或
因为入射光线与反射光线关于x轴对称，于是在上述方程中以
代替
得：
或
故入射直线l所在直线的方程是或
18、解：由
得：
即
当
时，曲线和有且只有一个交点，
由于曲线和有且只有一个交点，
从而
，解得：
故或
19、解法一：当所求圆的直径为直线与已知圆的相交弦时，圆的面积最小
依题意设所求圆的方程为
由得：
，所以
又圆心（a，b）在直线上，且两圆心的连线与已知直线垂直
所以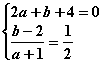
解得：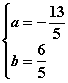
故所求圆的方程为
解法二：
设所求的圆的方程为
将方程配方得：
所以当
时，此面积最小，故满足条件的方程是
20、解：由得：
由对称，得圆心在直线上，即
，解得：k=2
又过P、Q两点的直线与直线
垂直，所以设过P、Q两点的直线方程为
，
由OP⊥OQ得：
代入得：
，整理得到：
（*）
由
得：
所以
代入（*）式解得：
故所求的直线方程是
或
21、解：依题意知：直线
的斜率不为0，且直线
的斜率一定存在，下面对
的斜率分情况讨论：
（1）当直线的斜率存在时，设线段中点（x，y），则
M（2x，0），N（0，2y），
由与垂直得：
，
整理得 
*
（2）当直线的斜率不存在时，
，M（a，0），N（0，b）
线段中点（
），满足方程 *
综上述，得B点轨迹方程为
22、解：由得：
设
，
（1）由得：
，（其中
）
故
（2）由恒成立知：
而
的最大值为
，故m的取值范围是
|