高二上期末考试模拟试题二
数 学
（测试时间：120分钟 满分150分）
一． 选择题（12×5分=60分，每小题给出的四个选项中，只有一项是符合题目要求的，将正确结论的代号填入后面的表中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．
若
，且
,
,则有
A． p>q B. p<q C. p=q D. 由m、n的取值决定
2． 请看下列推理过程，共有三个推理步骤
其中错误步骤的个数有
A． 0 B. 1 C. 2 D. 3
3. 直线kx-y+1-3k=0, 当k变动时,所有直线都通过定点
A. (0,0) B (0,1) C. (3,1) D. (2,1)
4. 若a、b、c
R,且a-b<c , 则
A． a<b+c B. a>b+c C. a<b+c D. a>b-c
5. 直线
的倾斜角是
A. 
B. 
C. 
D. 
6．若直线
与直线
互相垂直，则
A a=2 B. a=-2 C. a=2或-2 D. a=2或0或-2
7. 若直线
被圆
所截得的弦长为
,则a为
A . 
B. 1或3 C. –2或6
D. 0或4
8不等式组
表示的平面区域是
A. B. C. D.
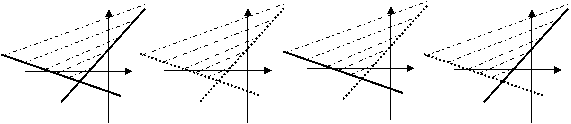
9. 若方程
表示双曲线,则m的取值范围是
A. m<4 B. m>9 C. –4<m<9 D. m<4或m>9
10. 从椭圆短轴的一个端点看长轴两个端点的视角为
,那么此椭圆的离心率为
A. 
B. 
C. 
D. 
11. 如果椭圆
上一点M到此椭圆一个焦点
的距离为2, N是
的中点,O是坐标原点,则ON的长为
A. 2
B. 4
C. 8 D. 
12. 抛物线
上的点到直线y=2x+b的最短距离为
,则b的值为
A. –6 B. 4 C. 8 D. –4或6
二.填空题(4×4分=16分)
13. 设
, 则函数
的最大值是
14. 若不等式
的解集为
, 则不等式
的解集为
15. 光线从点A(-3,4)出发射到X轴上,被X轴反射到Y轴上,又被Y轴反射后到点B(-1,6),则光线所经过的路途长
16. 随着人类物质文明进程的加快，各种形态、各种功能的空中缆线也日益增多。我们知道，两端挂起的缆线下垂近似成抛物线形。设某处缆线两端各离地面20米，两端间的水平距离是80米，缆线的中点（即抛物线的顶点）离地面6米，则离两端30米处缆线的高度是
三．解答题（本大题共6道小题，共74分，解答题应写出文字说明，演示步骤或证明过程）
17．（本小题满12分）
解不等式：
18．（本小题满12分）
已知直线
：
，直线
经过点P（0，1）且到的角为
，求直线的 方程.
19.（本小题满12分）
已知椭圆的准线平行于X轴,长轴长是短轴长的3倍, 且过点(2,3),求椭圆的标准方程.
20. (本小题满12分)
已知: x > y >0 , 且xy=1, 若
恒成立,求:实数a的取值范围.
21.（本小题满12分）
A、B、C是我方三个炮兵阵地,A在B的正东,相距6千米,C在B的北偏西相距4千米,P为敌炮阵地,某时刻,A发现P处的某种信号,由于B、C两地比A地距P地远,因此4秒后,B、C才同时发现这一信号(设该信号的传播速度为1千米/秒)
① 建立适当的坐标系,确定P的位置(即求出P的坐标);
② A若炮击P地,求炮击的方向.
22. (本小题满14分)
已知圆
:
和双曲线
,直线L同时满足下列两个条件:
①
与双曲线
相交; ② 与圆相切,且切点是L与相交所得弦的中点, 求直线L的方程.
y
O
x