高二上期末考试模拟试题二十
数 学
（测试时间：120分钟 满分150分）
一、选择题（每小题5分，共60分）
1、过点P(—1，2)的直线l与x轴、y轴分别交于A、B两点，且P恰好为AB的中点，则AB的斜率为…………………………………………………………………………………………（ ）
A、
B、
C、-2
D、2
2、若a>b>c，则一定成立的不等式是 ……………………………………………………（ ）
A、ac>bc
B、ab>ac C、a—c>b—c D
3、如果原点在直线l的射影为点(a, b)（a2+b2≠0），则直线l的方程为………………（ ）
A、bx+ay= a2+b2 B、ax+by= a2+b2 C、bx-ay= a2-b2 D、ax-by= a2-b2
4、若a、b是正数，则
、
、
、
这四个数的大小顺序是 …（ ）
A、≤≤≤
B、≤≤≤
C、≤≤≤
D、≤≤≤
5、已知直线l1：x+my+5=0和直线l2：x+ny+p=0，则l1和l2关于y轴对称的充要条件是 …（ ）
A、
B、p=-5 C、m=-n且p=-5 D、
6、不等式（x2-2x-3）(x2-4x+4)<0的解集是 …………………………………………………（ ）
A、{xx<-1或x>3} B、{x-1<x<3} C、{xx<-3或x>1} D、{x-1<x<2或2<x<3}
7、若直线(2a+5) x+(a-2) y+4=0与直线(2-a) x+(a+3) y-1=0互相垂直，则…………………（ ）
A、a=2 B、a=-2 C、a=2或a=-2 D、a=2,0,-2
8、不等式组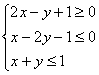
表示的平面区域为某……………………………………………（ ）
A、正三角形及其内部 B、等腰三角形及其内部
C、在第一象限内的一个无界区域 D、不包含第一象限内的点的一个有界区域
9、线性目标函数z =2x-y在线性约束条件
下，取最小值时的最优解是 …………（ ）
A、（1，1） B、（-1，1） C、（-1，-1） D、（1，-1）
10、若不等式
的解集为
，则a的值为…………………………（ ）
A、
B、
C、
D、
11、设a, b, k, p分别表示同一直线的横截距，纵截距，斜率和原点到直线的距离，则有 （ ）
A、
B、
C、
D、
12、当x-2<a时，不等式x2-4<1成立，正数a的取值范围是 ………………………………（ ）
A、
B、
C、
D、
二、填空题（每小题4分，共16分）
13、直线y=1与直线
的夹角为
。
14、若-1<a<b<1, -2<c<3，则（a-b）·c的取值范围是 。
15、点（-2, t）在直线2x-3y+6=0的上方，则t的取值范围是 。
16、若a、b∈R，则下列不等式：①a2+3>2a，②a2+b2≥2（a-b-1），③a5+b5>a3b2+a2b3，④
中一定成立的是
。
三、解答题（共6小题，共74分）
17、（本小题满分12分）解不等式2x+1+x-2>4.
18、（本小题满分12分）△ABC的三个顶点A（-3, 0），B(2, 1)，C(-2, 3). 求（1）BC所在直线的方程； （2）BC边上中线AD所在直线的方程； （3）BC边的垂直平分线DE的方程.
19、（本小题满分12分）设a>0,
b>0，求证
.
20、（本小题满分12分）已知A(0,3)，B (-1,0)，C (3,0)，求D点的坐标，使四边形ABCD是等腰梯形.
21、（本小题满分12分）某企业生产A、B两种产品,生产每一吨产品所需的劳动力、煤、电耗及利润如下表：
| 产品品种 | 劳动力 (个) | 煤 (吨) | 电 (千瓦) | 利润 (万元/吨) | 现因条件限制，该企业仅有劳动力200个，煤360吨，供电局只供电300千瓦，试问该企业生产A、B两种产品各多少吨才能获得最大利润？ |
| A产品 | 4 | 9 | 3 | 7 | |
| B产品 | 5 | 4 | 10 | 12 |
22、（本小题满分14分）设计一幅宣传画，要求画面面积为4840cm2，画面的宽与高的比为λ(λ<1)，画面的上、下各留8cm空白，左右各留5 cm空白。怎样确定画面的高与宽的尺寸，能使宣传画所用纸张面积最小？如果
，那么λ为何值时，能使宣传画所用纸张的面积最小？
参 考 答 案
一、选择题（共60分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | C | B | C | C | D | C | B | B | C | A | B |
二、填空题（共16分）
13、 60° 14、 （-6， 4） 15、
16、 ① ②
三、解答题（共74分）
17、解 ①当
时，原不等式可化为：
…………3分
②当
时，原不等式可化为：
……… 6分
③当x>2时，原不等式可化为：
…9分
∴综上得，原不等式的解集为{x｜x<-1, 或x>1} 资料 ………………………………12分
18、解（1）因为直线BC经过B（2，1）和C（-2，3）两点，由两点式得直线BC的方程：
，即
. ………………………………………………………………………4分
(2)设BC中点D的坐标为（x, y），则
.BC边的中线AD过点A（-3,0），D（0,2）两点，由截距式得AD所在直线方程为
，即
……8分
(3)BC的斜率
,则BC的垂直平分线DE的斜率
,由斜截式得直线DE的方程为
. …………………………………………………………………………………… 12分
19、证明：左边—右边
………………………………… 3分
………………………………………7分
…………………………………………………………… 11分
∴原不等式成立. ………………………………………………………………………… 12分
20、解：设D（x，y），若AB//CD，则KAB=KCD，且｜AD｜=｜BＣ｜
|
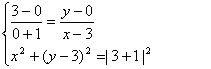
由①②解得
…………………………………………………………………５分
若AD//BC，则KAD=KBC且｜AB｜=｜CD｜
|
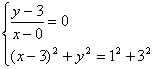
解③④得D（2，3） ………………………………………………………10分
故D点的坐标是
或（2，3）.
………………………………………12分
21、解：设该企业生产A种产品x吨，B种产品y吨，获得的利润为z万元.
则有：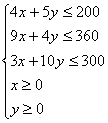
，且z=7x+12y ………………………………………5分
作出可行域。解方程组
，得A（20，24） …………………………8分
作直线l：7x+12y=0，把直线l向右上方平移至过A点时，z最大. ………………10分
答：生产甲种产品20吨，乙种产品24吨，能使利润达到最大值. ………………12分
22、解：设画面高为x cm，宽为λx cm，则λx2=4840，设纸张面积为S，则有
………3分
当且仅当
时，即
时，S取最小值.
此时，高
cm，宽
cm. …………………………5分
如果，则
，故等号不能成立. ………………………………………6分
设
，则
故
又
，
，
上是增函数，
…………………………………………………9分
，当
时，S(λ)取得最小值. ………………………………11分
答：画面高为88cm，宽55cm时，S(λ)取得最小值.如果，当时，所用纸张面积最小.…12分
|