高二上期末考试模拟试题五
数 学
(测试时间:120分钟 满分150分)
一、选择题(50分)
1.设集合![]() ,
,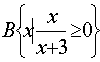 ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.抛物线![]() 上一点
上一点![]() 的纵坐标为4,则点
的纵坐标为4,则点![]() 与抛物线焦点的距离为( )
与抛物线焦点的距离为( )
(A) 2 (B) 3 (C) 4 (D) 5
3.设a,b,c分别是△ABC中,∠A,∠B,∠C所对边的边长,则直线sinA·x+ay+c=0与bx-sinB·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
4.已知双曲线![]() -
-![]() =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为![]() (O为原点),则两条渐近线的夹角为 ( )
(O为原点),则两条渐近线的夹角为 ( )
A.30º B.45º C.60º D.90º
5.设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.函数y=ax2+1的图象与直线y=x相切,则a=( )
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)1
(D)1
7.设函数f(x)=ax2+bx+c(a>0),满足f(1-x)=f(1+x),则f(2x)与f(3x)的大小关系是( )
A.f(3x)>f(2x) B.f(3x)<f(2x)
C.f(3x)≥f(2x) D.f(3x)≤f(2x)
8.已知F1、F2是双曲线![]() 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
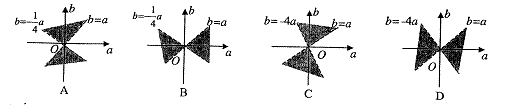 |
9.在
A.![]() B﹒
B﹒![]() C﹒
C﹒![]() D﹒
D﹒![]()
10.设![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.-3 D.
C.-3 D.![]()
二、填空题(24分)
11.抛物线y2=4x的准线方程是 ;焦点坐标是 .
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.若函数![]() 能用均值定理求最大值,则需要补充
能用均值定理求最大值,则需要补充![]() 的取值范围是
的取值范围是
13.已知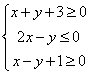 则
则![]() 的最大值为
的最大值为
14..从集合{1,2,3…,11}中任选两个元素作为椭圆方程![]() 中的m和n,则能组成落在矩形区域B={(x,y) x<11且y<9}内的椭圆个数为
中的m和n,则能组成落在矩形区域B={(x,y) x<11且y<9}内的椭圆个数为
15.已知点A在圆C:![]() 上运动,点B在以
上运动,点B在以![]() 为右焦点的椭圆
为右焦点的椭圆![]() 上运动,求AB的最大值
。
上运动,求AB的最大值
。
16.(2005江西卷理第16题,文第16题)
以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若![]() 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
 三、计算题(76分)
三、计算题(76分)
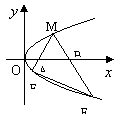
17. (13分)如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心轨迹方程。
18.(12分)解不等式:解关于![]() 的不等式:
的不等式:![]() (其中
(其中![]()
19. (12分)![]() 、
、![]() 、
、![]() 、
、![]() 四点都在椭圆
四点都在椭圆![]() 上,
上,![]() 为椭圆在
为椭圆在![]() 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,且
共线,且![]() .求四边形
.求四边形![]() 的面积的最小值和最大值.
的面积的最小值和最大值.
20.(13分)某人上午7:00时,乘摩托车以匀速V千米/时(4≤V≤20)从A港出发到相距50千米的B港去,然后乘汽车以匀速W千米/时(30≤W≤100)自B港向距300千米的C市驶去,要求在当天16:00时至21:00时这段时间到达C市.设汽车所需要的时间为X小时,摩托车所需要的时间为Y小时.
(1)作图表示满足上述条件的X,Y的范围;
(2)如果已知所要的经费:![]() (元),那么V,W分别是多少时所要的经费最少?此时需花费多少元?
(元),那么V,W分别是多少时所要的经费最少?此时需花费多少元?
21.(12分)已知二次函数![]() ,当
,当![]() 时,
时,![]() .
.
(1)求证:![]()
![]() ;
;
(2)若![]() ,求
,求![]() 的表达式.
的表达式.
22.(14分)22.(14分)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立直角坐标系.设
轴,建立直角坐标系.设![]() ,点F的坐标为
,点F的坐标为![]() .点G的坐标为
.点G的坐标为![]() .
.
(1)求![]() 关于t的函数
关于t的函数![]() 的表达式,并判断函数
的表达式,并判断函数![]() 的单调性.
的单调性.
(2)设△![]() 的面积
的面积![]() ,若
,若![]() 以为中心,
以为中心,![]() ,为焦点的椭圆经过点G,求当
,为焦点的椭圆经过点G,求当![]() 取最小值时椭圆的方程.
取最小值时椭圆的方程.
(3)在(2)的条件下,若点![]() 的坐标为
的坐标为![]() ,C,D是椭圆上的两点,
,C,D是椭圆上的两点,![]() , 求实数
, 求实数![]() 的取值范围.
的取值范围.
参考答案
一、选择题:1—5 DDCDD 6—10 BACBC
二、填空题:11﹒x=-1;(1,
0) 12﹒![]() 13. 26 14.90 15.
13. 26 14.90 15.![]() 16. ③④
16. ③④
三、17. 解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则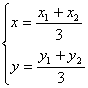 …(1)
…(1)
∵OA⊥OB ∴![]() ,即
,即![]() ,……(2)
,……(2)
又点A,B在抛物线上,有![]() ,代入(2)化简得
,代入(2)化简得![]()
∴![]()
所以重心为G的轨迹方程为![]()
(II)![]()
由(I)得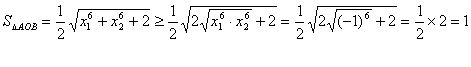
当且仅当![]() 即
即![]() 时,等号成立。
时,等号成立。
所以△AOB的面积存在最小值,存在时求最小值1;
18.解: ![]()
![]()
![]()
![]()
![]()
① 当![]() 时, 原不等式的解集为
时, 原不等式的解集为 ![]() ② 当
② 当![]() 时, 原不等式的解集为
时, 原不等式的解集为 ![]() ③ 当
③ 当![]() 时 原不等式的解集为
时 原不等式的解集为 ![]()
解:如图,由条件知MN和PQ是椭圆的两条弦,相交于焦点F(0,1),且PQ⊥MN,直线PQ、NM中至少有一条存在斜率,不妨设PQ的斜率为K,又PQ过点F(0,1),故PQ的方程为![]() =
=![]() +1
+1
将此式代入椭圆方程得(2+![]() )
)![]() +2
+2![]() -1=0
-1=0
设P、Q两点的坐标分别为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),则
),则
![]()
从而![]()
亦即![]()
(1)当![]() ≠0时,MN的斜率为-
≠0时,MN的斜率为-![]() ,同上可推得
,同上可推得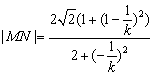
故四边形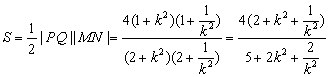
令![]() =
=![]() 得
得![]()
∵![]() =
=![]() ≥2
≥2
当![]() =±1时
=±1时![]() =2,S=
=2,S=![]() 且S是以
且S是以![]() 为自变量的增函数
为自变量的增函数
∴![]()
②当![]() =0时,MN为椭圆长轴,MN=2
=0时,MN为椭圆长轴,MN=2![]() ,PQ=
,PQ=![]() 。∴S=
。∴S=![]() PQMN=2
PQMN=2
综合①②知四边形PMQN的最大值为2,最小值为![]() 。
。
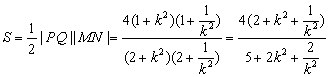
令![]() =
=![]() 得
得![]()
∵![]() =
=![]() ≥2
≥2
当![]() =±1时
=±1时![]() =2,S=
=2,S=![]() 且S是以
且S是以![]() 为自变量的增函数
为自变量的增函数
∴![]()
②当![]() =0时,MN为椭圆长轴,MN=2
=0时,MN为椭圆长轴,MN=2![]() ,PQ=
,PQ=![]() 。∴S=
。∴S=![]() PQMN=2
PQMN=2
综合①②知四边形PMQN的最大值为2,最小值为![]() 。
。
20.解:(1)依题意得:![]() ,又
,又![]() ,所以
,所以![]() ,而
,而![]() ,所以满足条件的点的范围是图中阴影部分:
,所以满足条件的点的范围是图中阴影部分:
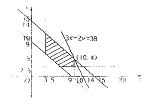 (2)
(2)![]() 作出一组平行直线
作出一组平行直线![]() (
(![]() 为参数),由图可知,当直线
为参数),由图可知,当直线![]() 经过点
经过点![]() 时,其在
时,其在![]() 轴上截距最大,此时
轴上截距最大,此时![]() 有最小值,即
有最小值,即![]() 当时,
当时,![]() 最小此时
最小此时![]() ,
,![]() 元
元
21.(1)由已知得![]() ,
,![]()
∴![]() ∴
∴![]()
(2)若![]() ,则
,则![]() 在
在![]() 为增函数,∴
为增函数,∴![]() ∴
∴![]() 与
与![]() 矛盾;若
矛盾;若![]() ,则
,则![]() 在
在![]() 为减函数,∴
为减函数,∴![]() 与已知矛盾。所以
与已知矛盾。所以![]() ,从而由
,从而由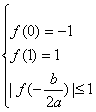 解得
解得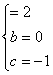 .
∴
.
∴![]()
22.(1)由题意得:![]() ,则:
,则:![]() ,解得:
,解得:![]() 所以
所以![]() 在
在![]() 上单调递增。
上单调递增。
(2)由![]() 得
得![]() ,点
,点![]() 的坐标为
的坐标为![]() 当
当![]() 时,
时,![]() 取得最小值,此时点
取得最小值,此时点![]() 的坐标为
的坐标为![]() 、
、![]() 由题意设椭圆的方程为
由题意设椭圆的方程为![]() ,又点
,又点![]() 在椭圆上,解得
在椭圆上,解得![]() 或
或![]() (舍)故所求的椭圆方程为
(舍)故所求的椭圆方程为![]()
(3)设![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 则
则![]() 由
由![]() 得
得![]() ,
,![]() 又点
又点![]() 在椭圆上
在椭圆上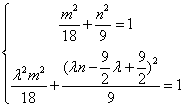 消去
消去![]() 得
得![]()
![]() 解得
解得![]() 又
又![]() 实数
实数![]() 的范围是
的范围是![]()