高二上期末考试模拟试题六
数 学
(测试时间:120分钟 满分150分)
一、选择题(本大题共10小题,每小题5分,共50分)
1.不等式![]() >
> ![]() 的解集是
( )
的解集是
( )
A.{x x ¹ –1} B.{ x x > –1 } C.{ x x < 0且x ¹ –1 } D.{x –1 < x < 0 }.
2.已知曲线C1: y= –x 2 +4x–2 , C2: y 2 = x, 若C1、C2 关于直线l对称, 则l的方程是( )
A.x + y + 2 = 0 B.x + y –2 = 0 C.x – y + 2 = 0. D.x – y – 2 = 0.
3.当![]() 时,方程
时,方程![]() 的解的个数是
( )
的解的个数是
( )
A.0 B.1 C.2 D.3
4.已知 – 1< x + y < 3,且2 < x – y < 4,则2x +3y的取值范围是 ( )
A.(–![]() ,
,![]() ) B.(–
) B.(–![]() ,
,![]() ) C.(–
) C.(–![]() ,
,![]() ) D.(–
) D.(–![]() ,
,![]() )
)
5.若抛物线![]() 上横坐标为3的点到焦点的距离等于5,则
上横坐标为3的点到焦点的距离等于5,则![]() 等于 ( )
等于 ( )
A.1.5 B.2 C.4 D.8
6.直线![]() 与直线
与直线![]() 互相垂直,
互相垂直,![]() R,则
R,则![]() 的最小值
的最小值
为 ( )
A.1 B.2 C.3 D.4
7.把曲线C1:![]() 按向量
按向量![]() 平移后得到曲线C2,曲线C2有一条准线为
平移后得到曲线C2,曲线C2有一条准线为
![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.3 D.-3
C.3 D.-3
8.圆心在抛物线![]() 上,且与
上,且与![]() 轴和该抛物线的准线都相切的一个圆的方程是( )
轴和该抛物线的准线都相切的一个圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 9.已知点(
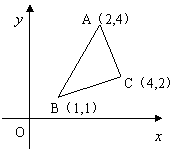
9.已知点(![]() )在如图所示三角形及其内部运动,
)在如图所示三角形及其内部运动,
如果使![]() (
(![]() )取得最大值的
)取得最大值的
点(![]() )有无穷多个,则
)有无穷多个,则![]() ( )
( )
A.![]() B.1 C.6 D.3
B.1 C.6 D.3
10.若椭圆![]() 与双曲线
与双曲线![]()
有相同的焦点F1、F2,P是两曲线的一个交点,则![]() 的面积是 ( )
的面积是 ( )
A.4 B.2 C.1 D.![]()
二、填空题(本大题共6小题,每小题4分,共24分。
11. 一次化学实验中需要用天平称出20g氧化铜粉末, 某同学发现自己所用的天平是不准的(其两臂不等长),因此, 他采用下列操作方法:选10g的法码放入左盘, 置氧化铜粉末于右盘使之平衡,取出氧化铜粉末, 然后又将10g法码放于右盘, 置氧化铜粉末于左盘, 平衡后再取出.他这样称两次得到的氧化铜粉末之和应该 20g。(选用“大于”,“小于”,“等于”)
12、不等式![]() 的解集是
。
的解集是
。
13.椭圆![]() 的焦点在
的焦点在![]() 轴上,则
轴上,则![]() 的取值范围是
.
的取值范围是
.
14.已知椭圆![]() 与双曲线
与双曲线![]() (
(![]() )有相同的焦点F1、F2、P是两曲线的一个交点,则
)有相同的焦点F1、F2、P是两曲线的一个交点,则![]() 等于 .
等于 .
15.已知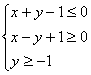 ,且
,且![]() ,则
,则![]() 的最小值为 .
的最小值为 .
16.对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点; ②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点; ④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
三、解答题(本大题共6题,共76分)
17.(本小题满分12分)已知圆C:![]() ,直线
,直线![]() :
:![]() ,
,
(1)求证对![]() R,直线
R,直线![]() 和圆C总相交;
和圆C总相交;
(2)设直线![]() 和圆C交于A、B两点,当
和圆C交于A、B两点,当![]() 取得最大值时,求直线
取得最大值时,求直线![]() 的方程.
的方程.
18.(本小题满分13分)已知![]() .设
.设![]() 函数
函数![]() 在R上单调递减.
在R上单调递减.![]() 不等式
不等式![]()
的解集为R. 如果![]() 和
和![]() 有且仅有一个正确,求
有且仅有一个正确,求![]() 的取值范围.
的取值范围.
19.(本小题满分13分)如图,长为6的线段PQ的端点分别在射线![]() 和
和![]()
上滑动,点M在线段PQ上,且![]() .
.
(1)求点M的轨迹方程;
(2)若点M的轨迹与![]() 轴、
轴、![]() 轴分别交于点A,B,求四边形OAMB面积的最大值.
轴分别交于点A,B,求四边形OAMB面积的最大值.
20.(本小题满分12分)已知抛物线 y 2 = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是
坐标原点.
(1)求证: OA^OB; (2)当△OAB的面积等于![]() 时, 求k的值.
时, 求k的值.
21.(本小题满分12分)A、B、C是我军三个炮兵阵地,A在B的正东方向相距6千米,C在B的北30°西方向,相距4千米,P为敌炮阵地.某时刻,A发现敌炮阵地的某信号,由于B、C比A距P更远,因此,4秒后,B、C才同时发现这一信号(该信号的传播速度为每秒1千米).若从A炮击敌阵地P,求炮击的方位角.
22 (本题满分14分)
|
|
已知a , b都是正数,△ABC是平面直角坐标系xOy内, 以两点A ( a , 0 )和B ( 0 , b )为顶点的正三角形,且它的第三个顶点C在第一象限内.
(1)若△ABC能含于正方形D = { ( x , y ) 0 £ x £ 1, 0£ y £ 1}内, 试求 变量 a , b 的约束条件,并在直角坐标系aOb内内画出这个约束等条件表示的平面区域;
(2)当( a, b )在(1)所得的约束条件内移动时,求△ABC面积S的最大值,并求此时(a , b )的值.
参考答案
一.选择题 (本大题共12小题, 每小题5分, 共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | D | D | C | B | C | D | B | C |
二.填空题(本大题有4小题, 每小题4分, 共16分)
11、大于 12、![]() 13.(2,4) 14.
13.(2,4) 14. ![]() 15.
15. ![]() 16. ①②
16. ①②
三、解答题(本大题共6题,共74分)
17.(1)证明:因圆C的圆心为C(0,1),半径![]() ,
,
所以圆心C到直线![]() 的距离为
的距离为![]() ,
,
命题得证。
另析:直线![]() :
:![]() 恒过过定点P
恒过过定点P![]() ,可判明在圆内,即证明直线
,可判明在圆内,即证明直线![]() 和
和
圆C总相交。
(2)当![]() 最小时
最小时![]() 最大,而
最大,而![]() 时
时![]() 最小,此时
最小,此时![]() 的方程为
的方程为![]() .
.
18. [分析] 此题虽是一道在老教材之下的高考试题,但揭示了“解不等式”一类高考试题的命题方向.在新教材中,绝对值不等式的解法和二次不等式的解法与集合运算、命题判断都有一定联系,属于对于学生提出的基本要求内容的范畴,本题将这几部分知识内容有机地结合在一起,在考查学生基础知识、基本方法掌握的同时,考查了学生命题转换,分类讨论等能力,在不同的方法下有不同的运算量,较好地体现出了“多考一点想,少考一点算”的命题原则.
解答:函数![]() 在R上单调递减
在R上单调递减![]() ,
,
不等式![]() 的解集为R
的解集为R![]() 函数
函数![]() 在R上恒大于1,
在R上恒大于1,
∵![]()
∴函数![]() 在R上的最小值为
在R上的最小值为![]() ,
,
∴不等式![]() 的解集为R
的解集为R![]()
![]() ,即
,即![]() ,
,
若![]() 正确,且
正确,且![]() 不正确,则
不正确,则![]() ;
;
若![]() 正确,且
正确,且![]() 不正确,则
不正确,则![]() ;
;
所以![]() 的取值范围为
的取值范围为![]() .
.
19.(1)设P(![]() ),Q(
),Q(![]() ),M(
),M(![]() ),
),
由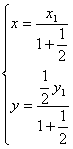 得
得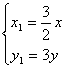 代入
代入![]() 得
得![]() .
.
(2)设M(![]() ),其中
),其中![]() ,
,
S=![]() ,计算S的平方,可得所求最大值为
,计算S的平方,可得所求最大值为![]() .
.
20.解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意,
∴k ¹ 0由y = k (x+1)得x = ![]() –1 代入y 2 = – x 整理得: y 2 +
–1 代入y 2 = – x 整理得: y 2 +![]() y – 1 = 0 ,
y – 1 = 0 ,
设A (x 1 , y 1),
B (x 2 , y 2) 则y 1 + y 2 = –![]() , y 1y
2 = –1.
, y 1y
2 = –1.
∵A、B在y 2
= – x上, ∴A (–![]() , y 1 ), B (–
, y 1 ), B (–![]() , y 2 ) ,
, y 2 ) ,
∴ kOA·kOB =![]() =
=![]() = – 1 .
= – 1 .
∴ OA^OB.
(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴OE = 1 ,
S△OAB =![]() OE( y 1 + y 2 ) =
OE( y 1 + y 2 ) =![]() y 1 – y 2 =
y 1 – y 2 =![]()
![]() =
=![]() , 解得k = ±
, 解得k = ±![]() .
.
21.以线段AB的中点为原点,正东方向为![]() 轴的正方向建立直角坐标系,
轴的正方向建立直角坐标系,
则![]() 依题意
依题意 ![]()
![]() 在以A、B为焦点的双曲线的右支上.这里
在以A、B为焦点的双曲线的右支上.这里![]() .
.
其方程为 ![]()
又 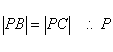 又在线段AB的垂直平分线上
又在线段AB的垂直平分线上![]()
由方程组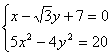 解得
解得  即
即 ![]()
由于![]() ,可知P在北30°东方向.
,可知P在北30°东方向.
22解: (1)顶点C是以A、B为圆心AB为半径的两圆在第一象限的交点,由圆A: ( x – a)2 + y2 = a2 + b2
, 圆B: x2 + ( y – b )2 = a2
+ b2 . 解得 x = ![]() , y =
, y = ![]() ,∴C(
,∴C(![]() ,
,![]() ) △ABC含于正方形D内,即三顶点A,B,C含于区域D内时,
) △ABC含于正方形D内,即三顶点A,B,C含于区域D内时,
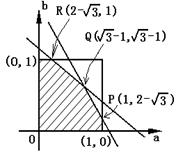 ∴
∴ 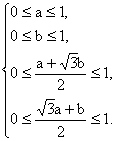 这就是 ( a , b )的约束条件. 其图形为右图的六边形,∵a > 0 , b > 0 , ∴图中坐标轴上的点除外.
这就是 ( a , b )的约束条件. 其图形为右图的六边形,∵a > 0 , b > 0 , ∴图中坐标轴上的点除外.
(2)∵△ABC是边长为![]() 的正三角形,∴ S =
的正三角形,∴ S = ![]() ( a2 + b2 )在(1)的条件下, 当S取最大值等价于六边形图形中的点(
a, b )到原点的距离最大,由六边形中P、Q、R相应的OP、OQ、OR的计算.OP2
= OR2 = 12 + ( 2 –
( a2 + b2 )在(1)的条件下, 当S取最大值等价于六边形图形中的点(
a, b )到原点的距离最大,由六边形中P、Q、R相应的OP、OQ、OR的计算.OP2
= OR2 = 12 + ( 2 – ![]() )2 = 8 – 4
)2 = 8 – 4![]() ;OQ2 = 2(
;OQ2 = 2(![]() – 1)2 = 8 – 4
– 1)2 = 8 – 4![]() . 知: 当 ( a , b ) = ( 1, 2 –
. 知: 当 ( a , b ) = ( 1, 2 –![]() ), 或(
), 或(![]() – 1,
– 1, ![]() – 1), 或( 2 –
– 1), 或( 2 –![]() , 1 )时, Smax =2
, 1 )时, Smax =2![]() – 3.
– 3.
一.