高二数学上学期复习测试试题
第Ⅰ卷 选择题 (共50分)
一、选择题(本大题共10小题,每题5分,共50分,每小题给出的4个选项中,只有一选项是符合题目要求的)
1.
等差数列![]() 中,
中,![]() = 2 ,则该数列的前5项的和为
(D)
A.32
B.20 C.16
D.10
= 2 ,则该数列的前5项的和为
(D)
A.32
B.20 C.16
D.10
2.
抛物线y = -2x2的准线方程是 (C)
A.x=-![]() B.x=
B.x=![]() .C.y=
.C.y=![]() D.y=-
D.y=-![]()
3. 下列命题中,其“非”是真命题的是 (D)
A.∀x∈R ,x²-![]() x + 2 ≥ 0 ; B.∃x∈R ,3x-5 = 0 ;
x + 2 ≥ 0 ; B.∃x∈R ,3x-5 = 0 ;
C.一切分数都是有理数 ; D.对于任意的实数a,b,方程ax=b都有唯一解 .
4. 已知F1、F2是双曲线 ![]() (a>0,b>0)的两焦点,以线段F
(a>0,b>0)的两焦点,以线段F
A.4+![]() B.
B.![]() +1 C.
+1 C.![]() —1 D.
—1 D.![]()
5.方程![]() 表示的曲线是
( D)
表示的曲线是
( D)
A.圆 B.椭圆 C.双曲线 D.抛物线
6. 已知f(x) = x2 + 2x f1 (1) , 则f 1(0)= ( B)
A.0
B.-
7.设x,y是正实数,且满足x + 4y = 40,则lgx+lgy的最大值是 ( A )
A.2 B.
8. 已知数列{an},那么“对任意的n∈N*,点 Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列” 的 ( B)
A.必要不充分条件 ![]() B. 充分不必要条件 C. 充要条件 D. 既不充分又不必要条件
B. 充分不必要条件 C. 充要条件 D. 既不充分又不必要条件
9.已知x, y满足约束条件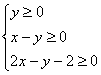 , 则
, 则![]() 的取值范围为是
(D)
的取值范围为是
(D)
A.〔 —1,![]()
![]() 〕 B.〔-
〕 B.〔-![]() ,
,![]() 〕 C. 〔 -
〕 C. 〔 -![]() ,+∞ ) D. 〔-
,+∞ ) D. 〔-![]() ,1)
,1)
10.设F1,F2是x2 +3y2 = 3椭圆的焦点,点P是椭圆上的点,若∠F1PF2=900,则这样的点P有( D)
A.0个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题 (共100分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在答题卡的横线上)
11.函数y = ![]() 的定义域为 _ 〔-2,1〕 __
的定义域为 _ 〔-2,1〕 __
12.过点P(-1,2 ) 且与曲线y=3x2—4x+ 2在点M(1,1)处的切线平行的直线方程是 y= 2x +4
13已知m,n,m+n成等差数列,m,n,mn 成等比数列,则椭圆![]() 的离心率为____
的离心率为____![]() ___
___
14.在△ABC中∠A=600,b=1,S△ABC=![]() ,则
,则![]() =
= ![]()
三、解答题:(本大题共 6 小题,共 80分。解答应写出文字说明、证明过程或演算步骤。)
15.(本小题满分12分)求经过点P(―3,2![]() )和Q(―6
)和Q(―6![]() ,―7)且焦点在坐标轴上的双曲线的标准方程。
,―7)且焦点在坐标轴上的双曲线的标准方程。
解:依题意,设双曲线方程为Ax2-By2=1(AB>0)---------3分
∵双曲线过点P(―3,2![]() )和Q(―6
)和Q(―6![]() ,―7)
,―7) ![]()
∴ ![]() ------------7分
------------7分
解得:A=-![]() B=-
B=-![]() ----------10分
----------10分
故双曲线方程为 ![]() --------12分
--------12分
(若设为标准方程, 则需讨论焦点所在的轴)
16. (本小题满分12分)已知p:x < -2,或x > 10;q: ![]() ≤x≤
≤x≤![]() ;若¬p是q的充分而不必要条件,求实数
;若¬p是q的充分而不必要条件,求实数![]() 的取值范围。
的取值范围。
解:∵ p:x < -2,或x > 10;q:
![]() ≤x≤
≤x≤![]()
∴¬p: -2≤ x≤ 10 --------------------------3分
∵¬p![]() q
q
∴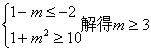 ---------------8分
---------------8分
又∵q ![]() ¬p ∴m
¬p ∴m![]() 3
3
∴m的取值范围为(3,+∞) ---------------------12分
17.(本小题满分14分)某银行准备新设一种定期存款业务,经测算:存款量与存款利率的平方成正比,比例系数为k(k>0),贷款的利率为4.8%,又银行吸收的存款能全部放贷出去。
(1)若存款利率为x,x∈(0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x)与存款利率x之间的关系式;
(2)存款利率为多少时,银行可获得最大收益?
解:(1)由题意知,存款量g(x)= kx2 ---------------------------------------2分
银行应支付的利息h(x)= xg(x)= kx3 ------------------4分
(2)设银行可获得的利益为y,则y = 0.048kx2-kx3 -------------------6分
y 1 =0.096kx-3kx2
令y 1= 0 即0.096kx-3kx2=0 解得:x=0.032 或 x=0(舍去)---------9分
当x∈(0,0.032)时,y 1>0
当x∈(0.032,0.048)时,y 1<0
∴当x=0.032时,y取得最大值 -----------------------------------------13分
故当存款利率为3.2%时,银行可获得最大利益。-------------------------14分
18.(本小题满分14分)函数f(x)= 4x3+ax2+bx+5的图在x=1处的切线方程为y=-12x;
(1)求函数f(x)的解析式;
(2)求函数f(x)在 [—3,1]上的最值。
解:(1)f 1(x)= 12x2+2ax+b -----------------------------------2 分
∵y =f(x)在x=1处的切线方程为 y=-12x
∴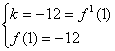 即
即![]()
解得:a=-3 b=-18 -------------------------------6分
∴f(x)=4x3―3x2―18x+5 ------------------------------------------------7分
(2)∵f 1(x)= 12x2-6x-18=6(x+1)(2x-3)
令f 1(x)=0 解得:x=-1或x=![]() --------------------------------------9分
--------------------------------------9分
∴ 当x<-1或x>![]() 时,f 1(x)>0
时,f 1(x)>0
当-1< x<![]() 时, f 1(x)<0
----------------------------------------11分
时, f 1(x)<0
----------------------------------------11分
∵ x∈[-3,1]
∴ 在[-3,1]上无极小值,有极大值f(-1)=16
又∵f(-3)=-
∴f(x)在[-3,1]上的最小值为-76,最大值为16。-------------------------------14分
19.(本小题满分14分)设椭圆![]() (a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。
(a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。
(1)求直线L和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上。
解:(1)由题意知,c=2及![]() 得 a=6
-----------------------------2分
得 a=6
-----------------------------2分
∴![]()
![]()
∴椭圆方程为![]() -----------------------4分
-----------------------4分
直线L的方程为:y-0=tan300(x+3)即y=![]() (x+3)------------6分
(x+3)------------6分
(2)由方程组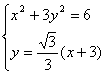 得
得 ![]() -----------------8分
-----------------8分
设A(x1,y1),B(x2,y2),则 x1+x2=-3 x1x2=![]()
∵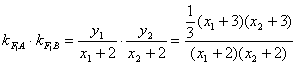
![]()
![]() ----------------12分
----------------12分
∴![]()
∴点F(-2,0)在以线段AB为直径的圆上 -----------------14分
(注:此问有多种解法)![]()
20.(本小题满分14分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 与2的等差中项,数列
与2的等差中项,数列![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
⑴求![]() 和
和![]() 的值;
的值;
⑵求数列![]() 的通项
的通项![]() 和
和![]() ;
;
⑶ 设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
解:(1)∵![]() 是
是![]() 与2的等差中项
与2的等差中项
∴![]() --------------------------------------------1分
--------------------------------------------1分
∴![]()
![]() -------------------------3分
-------------------------3分
(2)![]()
![]()
![]() .
.
![]()
∵a1=2
∴![]() -------------------------------------------------6分
-------------------------------------------------6分
![]()
∴![]() -----------8分
-----------8分
(3)![]()
![]() ------------10分
------------10分
![]()
因此:![]() ------------12分
------------12分
即:![]()
∴![]() ----------------------------------14分
----------------------------------14分