新课标高二数学同步测试(6)—(期中测试题2-1)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.判断下面命题的真值“如果明天太阳从西边出来,那么我就去死” ( )
A.假命题 B.真命题 C.不是命题 D.可真可假
2.若中心在原点,焦点在坐标上的椭圆短轴端点是双曲线y2-x2=1的顶点,且该椭圆的离心率与此双曲线的离心率的乘积为1,则该椭圆的方程为 ( )
A.![]() +y2=1 B.
+y2=1 B.![]() +x2=
+x2=![]() +y2=1 D.
+y2=1 D.![]() +x2=1
+x2=1
3.已知点![]() 在平面
在平面![]() 内,并且对空间任一点
内,并且对空间任一点![]() ,
,![]() 则
则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.双曲线x2-ay2=1的焦点坐标是 ( )
A.(![]() , 0) , (-
, 0) , (-![]() , 0) B.(
, 0) B.(![]() , 0), (-
, 0), (-![]() , 0)
, 0)
C.(-![]() , 0),(
, 0),(![]() , 0) D.(-
, 0) D.(-![]() , 0), (
, 0), (![]() , 0)
, 0)
5.设双曲线的焦点在x轴上,两条渐近线为![]() ,则该双曲线的离心率e ( )
,则该双曲线的离心率e ( )
A.5 B.![]() C.
C.![]() D.
D.![]()
6.在下列四个命题中
①已知A、B、C、D是空间的任意四点,则![]() .
.
②若{![]() }为空间的一组基底,则{
}为空间的一组基底,则{![]() }也构成空间的一组基底.
}也构成空间的一组基底.
③![]() .
.
④对于空间的任意一点O和不共线的三点A、B、C,若![]() (其中
(其中![]() ),则P、A、B、C四点共面.
),则P、A、B、C四点共面.
其中正确的个数是 ( )
A.
7.设a∈R,则a>1是![]() <1 的 ( )
<1 的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
8.设原命题:若a+b≥2,则a,b 中至少有一个不小于1.则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
9.在正方体AC1中, M为棱DD1的中点, O为底面ABCD的中心, P为棱A1B1上任意一点, 则直线OP与AM所成的角为 ( )
A.30° B.60° C.90° D.120°
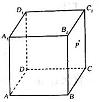 10.如图,在正方体ABCD-A1B
10.如图,在正方体ABCD-A1B
A.直线 B.圆
C.双曲线 D.抛物线
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.若方程x2-mx+
12.对于曲线C∶![]() =1,给出下面四个命题:
=1,给出下面四个命题:
①由线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<![]()
其中所有正确命题的序号为_______ ______.
13.已知四棱锥P-ABCD的底面为平行四边形, BD⊥AD, BD=2![]() , 又PD⊥底面ABCD, 二面角P-BC-A为60°, 则直线AD到平面PBC的距离为
.
, 又PD⊥底面ABCD, 二面角P-BC-A为60°, 则直线AD到平面PBC的距离为
.
14.直三棱柱ABC-A1B
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)写出下列命题的否命题:
(1)若![]() ,则关于
,则关于![]() 的方程
的方程![]() 有实数根;
有实数根;
(2)若x,y都是奇数,则x+y是奇数;
(3)若abc=0,则a,b,c中至少有一个为0;
(4)当c>0时,若a>b,则ac>bc.
16.(12分)如图,正方形![]() 与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,
与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,![]() , F、G分别是线段AE、BC的中点.
, F、G分别是线段AE、BC的中点.
|
17.(12分)设椭圆方程为![]() =1,求点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足
=1,求点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足![]() ,当l绕点M旋转时,求动点P的轨迹方程.
,当l绕点M旋转时,求动点P的轨迹方程.
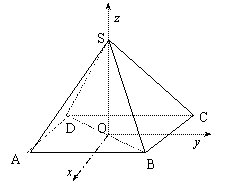 18.(12分)如图,正四棱锥
18.(12分)如图,正四棱锥![]() 的高
的高![]() ,底边长
,底边长![]() .求异面直线
.求异面直线![]() 和
和![]() 之间的距离.
之间的距离.
19.(12分)如图,正方体ABCD-A1B
(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB

20.(14分)若F1、F2分别为双曲线 -=1下、上焦点,O为坐标原点,P在双曲线的下支上,点M在上准线上,且满足:![]() ,
,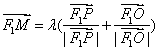 (>0).
(>0).
(1)求此双曲线的离心率;
(2)若此双曲线过N(,2),求此双曲线的方程
(3)若过N(,2)的双曲线的虚轴端点分别B1,B2(B2在x轴正半轴上),点A、B在双曲线上,且![]() ,求
,求![]() 时,直线AB的方程.
时,直线AB的方程.
参考答案
一、
1.A;解析:命题的条件一定为假,不可能成立;故原命题一定为假.
2.A;解析:由双曲线y2-x2=1的顶点坐标为![]() ,可得椭圆的b=1,在有双曲线的离心率为
,可得椭圆的b=1,在有双曲线的离心率为![]() ,从而得到椭圆的离心率为
,从而得到椭圆的离心率为![]() ,可得
,可得![]() ,所以选项为A.
,所以选项为A.
3.A;解析:四点M、A、B、C共面,使得![]() 中
中![]() ,从而可得
,从而可得![]() .
.
4.C;解析:将双曲线方程x2-ay2=1化为标准方程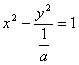 ,从而可得半焦距为
,从而可得半焦距为![]() ,可得答案.
,可得答案.
5.C;解析:由于焦点在x轴上的取向的渐近线方程![]() 为
为![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() 的值.
的值.
6.B;解析:正确的为①②;而命题③中![]() ,左边应为一个数乘的形式,右边则成了实数;命题④成立时当且仅当
,左边应为一个数乘的形式,右边则成了实数;命题④成立时当且仅当![]() 时成立.
时成立.
7.A;提示:![]() ;
;
8. A;提示:举例:a=1.2,b=0.3,则a+b=1.5<2,∴逆命题为假.
9.C;
10.D;
二、
11.![]() ;解析:方程两根x2-mx+
;解析:方程两根x2-mx+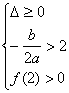 ,即可得到正确结果.
,即可得到正确结果.
12.③④;解析:由椭圆和双曲线方程的定义易得.
13.3;
14.![]() ;
;
三、
15.解:(1)若![]() ,则关于
,则关于![]() 的方程
的方程![]() 无实数根;
无实数根;
(2)若x,y不都是奇数,则x+y不是奇数;
(3)若abc≠0,则a,b,c中都不为0;
(4)当c>0时,若a≤b,则ac≤bc.
16.解:如图,正方形![]() 与等腰直角△ACB所在的
与等腰直角△ACB所在的
平面互相垂直,且AC=BC=2,![]() , F、G分别是线段AE、BC的中点.
, F、G分别是线段AE、BC的中点.
|
分析提示:以C为原点建立空间直角坐标系C—xyz
A(0,2,0) B(2,0,0) D(0,0,2)
G(1,0,0) F(0,2,1)
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() .
.
17.解:设P(x,y)是所求轨迹上的任一点,
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
![]() 4x2+y2-4=0
4x2+y2-4=0
由 得:
y=kx+1
(4+k2)x2+2kx-3=0,
x1+x2=-![]() y1+y2=
y1+y2=![]() ,
,
由![]() 得:
得:
(x,y)=![]() (x1+x2,y1+y2),
(x1+x2,y1+y2),
即: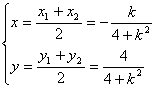
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程
所以动点P的轨迹方程为:4x2+y2-y= 0.
18.分析:建立如图所示的直角坐标系,则
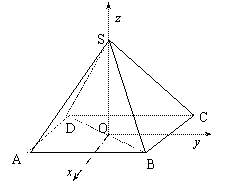
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
令向量![]() ,且
,且![]() ,则
,则![]() ,
,
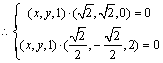 ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 异面直线
异面直线![]() 和
和![]() 之间的距离为:
之间的距离为:
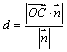
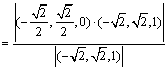
![]() .
.
19.解:(1)以A为原点,直线AB、AD、AA1为x轴、y轴、z轴建立空间直角坐标系,
不妨设正方体的棱长为1,且![]() ,则
,则![]()
![]()
于是![]()
由![]()
于是![]() ,可解得
,可解得![]()
所以当点F是CD的中点时,![]()
(2)当![]() 时,F是CD的中点,
时,F是CD的中点,![]()
平面AEF的一个法向量为![]()
而在平面C1EF中,![]()
所以平面C1EF的一个法向量为![]()
![]() ,
,![]()
又因为当把![]() ,
,![]() 都移向这个二面角内一点时,
都移向这个二面角内一点时,![]() 背向平面AEF,而
背向平面AEF,而![]() 指向平面C1EF
指向平面C1EF
故二面角C1―EF―A的大小为![]()
又![]() ,
, ![]()
![]() , 所以
, 所以![]()
![]() BA1与平面C1EF所成的角的大小为
BA1与平面C1EF所成的角的大小为![]() .
.
20.解:(1) ![]()
![]() ,∴PF1OM为平行四边形,
,∴PF1OM为平行四边形,
又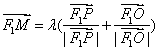 知M在∠PF1O的角平分线上,
知M在∠PF1O的角平分线上,
∴四边形PF1OM为菱形,且边长为![]() =c
=c
∴![]() =2a+
=2a+![]() =2a+c,由第二定义=e即=e,∴+1=e且e>1
=2a+c,由第二定义=e即=e,∴+1=e且e>1
∴e=2
(2)由e=2,∴c=
又N(,2)在双曲线上,∴-=1,∴a2=3∴双曲线的方程为-=1…7分
(3)由![]() 知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得
知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得
(3k2-1)x2-18k2x+27k2-9=0
由题知3k2-1≠0且△>0即k2> 且k2≠,
设交点A(x1,y1),B(x2,y2),![]() =(x1+3,y1),
=(x1+3,y1),![]() =(x2+3,y2),
=(x2+3,y2),
∵![]() ,∴
,∴![]() =0即x1x2+3(x1+x2)+9+y1y2=0
=0即x1x2+3(x1+x2)+9+y1y2=0
此时x1+x2=,x1·x2=9,
y1y2=k2(x1-3) (x2-3)=k2[x1x2-3(x1+x2)+9]= k2[18-]=-
∴9+3+9-=0,∴5 k2=1,∴k=±
∴AB的方程为y=±(x-3) .