新课标高二数学期末同步测试题
说明:本试卷分第一卷和第二卷两部分,第一卷50分,第二卷100分,共150分;答题时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.设a>0, b>0,则以下不等式中不恒成立的是 ( )
A.![]() ≥4 B.
≥4 B.![]() ≥
≥![]()
C.![]() ≥
≥![]() D.
D.![]() ≥
≥![]()
2.△ABC中,BC=1,![]() ,则AC的长度的取值范围为 ( )
,则AC的长度的取值范围为 ( )
A.(![]() )
B.(
)
B.(![]() ,1) C.[
,1) C.[![]() ] D.[
] D.[![]() ,1]
,1]
3.下列四个结论中正确的个数有 ( )
①y = sinx的图象关于原点对称;
②y = sin(x+2)的图象是把y = sinx的图象向左平移2个单位而得;
③y = sin(x+2)的图象是把y = sinx的图象向左平移2个单位而得;
④y = sin(x+2)的图象是由y = sin(x+2)( x≥0)的图象及y = -sin(x-2) ( x<0)的图象
组成的.
A.1个 B.2个 C.3个 D.4个
4.已知sinθ-cosθ=![]() , 则sin3θ- cos3θ的值为 ( )
, 则sin3θ- cos3θ的值为 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
5.平面直角坐标系中, O为坐标原点, 已知两点A(3, 1), B(-1, 3), 若点C满足
![]() =
=![]() , 其中α、β∈R且α+β=1, 则点C的轨迹方程为 ( )
, 其中α、β∈R且α+β=1, 则点C的轨迹方程为 ( )
A.3x+2y-11=0 B.(x-1)2+(y-2)2=5
C.2x-y=0 D.x+2y-5=0
6.已知钝角三角形的三边分别是a,a+1,a+2,其最大内角不超过120°,则a的取值范围是
( )
A .![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知f(x)=bx+1为x的一次函数, b为不等于1的常数,
且g(n)=![]() ,
,
设an= g(n)- g(n-1) (n∈N※), 则数列{an}是 ( )
A.等差数列 B.等比数列 C.递增数列 D.递减数列
8.定义![]() 为完全立方数,删去正整数数列1,2,3……中的所有完全立方数,得到一
为完全立方数,删去正整数数列1,2,3……中的所有完全立方数,得到一
个新数列,这个数列的第2005项是 ( )
A.2017 B.
9.已知θ为第二象限角,且![]() ,那么
,那么![]() 的取值范围是 ( )
的取值范围是 ( )
A.(-1,0) B.![]() C.(-1,1) D.
C.(-1,1) D.![]()
10.若对任意实数a,函数y=5sin(![]() π,x-
π,x-![]() )(k∈N)在区间[a,a+3]上的值
)(k∈N)在区间[a,a+3]上的值![]() 出现不少于4次且不多于8次,则k的值是 (
)
出现不少于4次且不多于8次,则k的值是 (
)
A.2 B.
第Ⅱ卷(非选择题,共100分)
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.![]() 的值为
.
的值为
.
12.已知等差数列{an}的公差d≠0, 且a1,
a3, a9成等比数列, 则![]() 的值是 .
的值是 .
13.已知向量![]() 向量
向量![]() , 则
, 则![]() 的最大值是
.
的最大值是
.
14.已知α、β是实数, 给出四个论断:
①α+β=α+β; ②α-β≤α+β; ③α>2![]() ,β>2
,β>2![]() ; ④α+β>5.
; ④α+β>5.
以其中的两个论断作为条件, 其余论断作为结论, 写出正确的一个 .
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分)。
15.(12分)在△ABC中,sinA+cosA=![]() ,AC=2,AB=3,求tanA的值和△ABC的面积.
,AC=2,AB=3,求tanA的值和△ABC的面积.
16.(12分)已知数列{an}的前n项和Sn满足2![]() =2aSn- an (n≥2)且a1=2, 求an和Sn.
=2aSn- an (n≥2)且a1=2, 求an和Sn.
17.(12分)已知向量![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 的值.
的值.
18.(12分)已知a、b∈R, a2+b2≤4, 求证:
19.(14分)△OBC的顶点坐标分别为(0,0)、(1,0)、(0,2), 设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n, Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),
![]()
(1)求![]() 及
及![]() ;
;
(2)证明![]()
(3)若记![]() 证明
证明![]() 是等比数列.
是等比数列.
20.(14分)已知奇函数f(x)的定义域为实数集R,且f(x)在![]() 上是增函数,是否存在这样的实数m,使
上是增函数,是否存在这样的实数m,使![]() 对所有的
对所有的![]() 均成立?若存在,求出适合条件的实数m的值或范围;若不存在,说明理由.
均成立?若存在,求出适合条件的实数m的值或范围;若不存在,说明理由.
高二新课标数学期末参考答案
一、BABCD DBADD
二、11.4;12.![]() ;13.4;14.①③
;13.4;14.①③![]() ②④ 或②③
②④ 或②③![]() ①④
①④
三、15.解:∵sinA+cosA=![]() cos(A-45°)=
cos(A-45°)=![]() ,
,
∴cos(A-45°)= ![]() . 又0°<A<180°, ∴A-45°=60°,A=105°.
. 又0°<A<180°, ∴A-45°=60°,A=105°.
∴tanA=tan(45°+60°)=![]() =-2-
=-2-![]() .
.
∴sinA=sin105°=sin(45°+60°)=sin45°×cos60°+cos45°×sin60°=![]() .
.
∴SABC=![]() AC·ABsinA=
AC·ABsinA=![]() ·2·3·
·2·3·![]() =
=![]() (
(![]() +
+![]() ).
).
16.解:an
=Sn- Sn+1 (n≥2) 代入题设等式得2 Sn·Sn-1= Sn-1-Sn,
即![]() -
-![]() =2,
=2,
∴数列{![]() }是以
}是以![]() 为首相, 2为公差的等差数列.
为首相, 2为公差的等差数列.
∴![]() =
=![]() +( n-1)·2=2 n-
+( n-1)·2=2 n-![]() =
=![]() ,
,
∴Sn=![]() (n≥2)
(n≥2)
∴an
=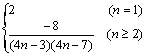
17.解:(1)![]()
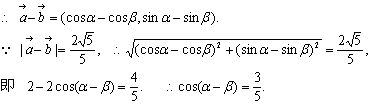
(2)![]()
![]()
![]()
18.解: ∵ a、b∈R, a2+b2≤4, ∴设a=rcosθ, b=rsinθ, 其中0≤r≤2.
∴ ![]() )≤5r2≤20.
)≤5r2≤20.
19.解:(Ⅰ)因为![]() ,所以
,所以![]() ,
,
又由题意可知![]() ,
,
∴![]() =
=![]()
=![]()
∴![]() 为常数列. ∴
为常数列. ∴![]()
(Ⅱ)将等式![]() 两边除以2,得
两边除以2,得![]()
又∵![]() , ∴
, ∴![]()
(Ⅲ)∵![]() =
=![]() =
=![]()
又∵![]() ∴
∴![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
20.解:∵f(x)为奇函数,∴f(-x)= -f(x), 又∵定义域为R,
∴令x=0,得f(0)=-f(0),得f(0)=0.
∵f(cos2θ-3)+f(
∴f(cos2θ-3)>-f(
∵f(x)在![]() 上是增函数,且f(x)为奇函数,∴f(x)在(-∞,+∞)上也为增函数。
上是增函数,且f(x)为奇函数,∴f(x)在(-∞,+∞)上也为增函数。
∴cos2θ-3>2mcosθ-
即cos2θ-mcosθ+![]() ,∴cosθ∈[0,1] ,
,∴cosθ∈[0,1] ,
令t=cosθ,t∈[0,1],则满足条件的m应该使不等式t2-mt+
设g(t)=t2-mt+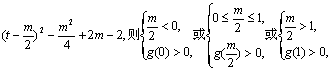
解之得![]() . 故满足条件的m存在,取值范围是
. 故满足条件的m存在,取值范围是![]()