新课标高二数学同步测试—(期末测试题2—2)
说明:本试卷分第一卷和第二卷两部分,第一卷74分,第二卷76分,共150分;答题时间120分钟.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.已知函数![]() 是 ( )
是 ( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数也是偶函数
2.设![]() ,
,![]() ,则
,则![]() 是
是![]() 成立的 ( )
成立的 ( )
A.充分条件,但不是必要条件; B.必要条件,但不是充分条件;
C.充分且必要条件; D.既不充分又不必要条件.
3. ![]() 的值等于 ( )
的值等于 ( )
A.1 B.-
4.使复数![]() 等于它的共轭复数的倒数的充要条件是 ( )
等于它的共轭复数的倒数的充要条件是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.椭圆的短轴上的两个三等分点与两个焦点构成一个正方形,则椭圆的离心率e为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果用C,R和I分别表示复数集,实数集和纯虚数集,其中C为全集,那么有( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7.长方体ABCD—A1B
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设F1、F2为双曲线![]() -y2=1的两焦点, 点P在双曲线上, 当△F1PF2面积为1时,
-y2=1的两焦点, 点P在双曲线上, 当△F1PF2面积为1时, ![]() 的值为 ( )
的值为 ( )
A.0 B.![]()
9.如果复数![]() 那么实数a的取值范围是 ( )
那么实数a的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知复数 ![]() 都是实数,且
都是实数,且![]() ),在复平面内,Z1、Z2所对应的点与原点组成的三角形是 ( )
),在复平面内,Z1、Z2所对应的点与原点组成的三角形是 ( )
A.锐角三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.若![]() .
.
12.若![]() .
.
13.平面直角坐标系下直线的方程为![]() ,请类比空间直角坐标系下平面的方程为
.
,请类比空间直角坐标系下平面的方程为
.
14.椭圆x2+![]() =1(0<a<1)上离顶点A(0, a)距离最远的点恰好是另一个顶点A′(0, - a), 则a的取值范围是
=1(0<a<1)上离顶点A(0, a)距离最远的点恰好是另一个顶点A′(0, - a), 则a的取值范围是
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知命题![]() :复数
:复数![]() 对应的点落在复平面的第二象限;命题
对应的点落在复平面的第二象限;命题![]() :以
:以![]() 为首项,公比为
为首项,公比为![]() 的等比数列的前
的等比数列的前![]() 项和极限为2.若命题“
项和极限为2.若命题“![]() 且
且![]() ”是假命题,“
”是假命题,“![]() 或
或![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围.
的取值范围.
16.(12分)(1) 设![]() ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤![]() ;
;
(2)设![]() ≤1,
≤1,![]() ,求证:
,求证:![]() ≤
≤![]()
17.(12分)用数学归纳法证明等式对所以n∈N*均成立.
![]()
18.(12分)设函数![]() ,其中
,其中![]() .
.
(I)解不等式![]() ;
;
(II)证明:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
19.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直. 点M在AC上移动,点N在BF上移动,若CM=BN=![]() .
.
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
20.(14分)椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )的准线
)的准线![]() 与x轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点.
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(Ⅲ)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于另一点M,
的直线与椭圆相交于另一点M,
证明:![]() .
.
参考答案
一、
1.B;
2.A
3.;答案:B
分析:![]()
![]()
另解:原式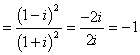
故选B.
4.B
5.A.
6.答案:D.
分析:由复数概念,如下图,
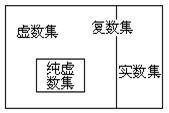
![]()
故选D.;
7.D;
8.A;
9.答案:D.
分析:由题意,
![]()
![]()
![]()
因此本题应选D.
10.
二、
11.![]() ;
;
12.![]() ;解析:当x≠1时,∵
;解析:当x≠1时,∵![]() ,
,
两边都是关于x的函数,求导得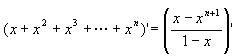
即![]() .
.
13.![]()
14.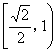
三、
15.解:命题![]() 有:
有: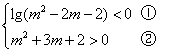
由①得:![]()
由②得:![]()
由上得满足P的m的取值范围是:![]() 或
或 ![]()
对命题![]() ,有:
,有:![]()
又![]()
得:![]() 且
且![]()
又命题“![]() 且
且![]() ”是假命题,“
”是假命题,“![]() 或
或![]() ”是真命题,则m的范围是
”是真命题,则m的范围是
![]()
16.解:⑴ x≤![]() 可化为
可化为![]() ≥0,令
≥0,令![]() =
=![]() ,
,
![]() ,由
,由![]() 得,
得,![]()
![]() =
=![]() =
=![]() ≤
≤![]() ≤
≤![]() ,
①
,
①
∴![]() ∈[-1,1],
∈[-1,1],![]() ≥0,即
≥0,即![]() ≥
≥![]() ②
②
由①、②得,![]() .
.
从而当![]() ≤1时,
≤1时,![]() =
=![]() ≥0,即x≤
≥0,即x≤![]() .
.
⑵ 由⑴知,对![]() ≤1,有
≤1,有![]() ≤
≤![]() ,(i=1,2,…,n)
,(i=1,2,…,n)
将这n个式子求和,得![]() ≤
≤![]() .
.
17.证明:i)当n=1时,左式=![]() ,右式=
,右式=![]() , ∴ 左式=右式,等式成立.
, ∴ 左式=右式,等式成立.
ii)假设当n=k(k∈N)时等式成立,
即![]() ,
,
则当n=k+1时,
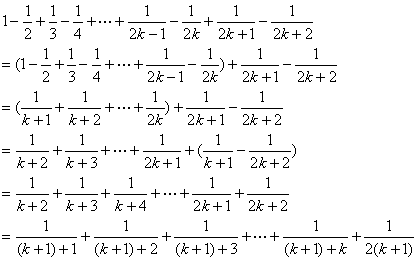
即n=k+1时,等式也成立,
由i) ii)可知,等式对n∈N均成立.
小结:在利用归纳假设论证n=k+1等式成立时,注意分析n=k与n=k+1的两个等式的差别.n=k+1时,等式左边增加两项,右边增加一项,而且右式的首项由![]() 变为
变为![]() .因此在证明中,右式中的
.因此在证明中,右式中的![]() 应与-
应与-![]() 合并,才能得到所证式.因而,在论证之前,把n=k+1时等式的左右两边的结构先作一分析是有效的.
合并,才能得到所证式.因而,在论证之前,把n=k+1时等式的左右两边的结构先作一分析是有效的.
由例1可以看出,数学归纳法的证明过程中,要把握好两个关键之处:一是f(n)与n的关系;二是f(k)与f(k+1)的关系.
18.解1:(I)分类讨论解无理不等式(略).
(II)作差比较(略).
解2:![]()
(i)当![]() 时,有
时,有![]() ,此时
,此时![]() ,函数
,函数![]() 在区间
在区间![]() 上是单调递减函数.但
上是单调递减函数.但![]() ,因此,当且仅当
,因此,当且仅当![]() 时,
时,![]() .
.
(ii)当![]() 时,解不等式
时,解不等式![]() ,得
,得![]() ,
,![]() 在区间
在区间![]() 上是单调递减函数.
上是单调递减函数.
解方程![]() ,得
,得![]() 或
或![]() ,
,
∵![]() ,
,
∴当且仅当![]() 时,
时,![]() ,
,
综上,(I)当![]() 时,所给不等式的解集为:
时,所给不等式的解集为: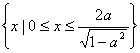 ;
;
当![]() 时,所给不等式的解集为:
时,所给不等式的解集为:![]() .
.
(II)当且仅当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上时单调函数.
上时单调函数.
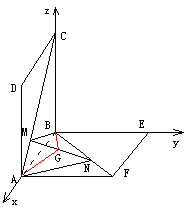
19.向量法)
解析:如图,建立空间直角坐标系B-xyz,
则A(1,0,0),C(0,0,1),E(0,1,0),F(1,1,0),
(I)![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
(II)由(I)知:![]()
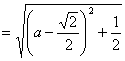
所以当![]() 时,MN的长最小,此时MN=
时,MN的长最小,此时MN=![]() .
.
(III)由(II)知,当MN的长最小时,![]() ,
,
此时M、N分别是AC、BF的中点.
取MN的中点G,连结AG、BG,易证∠AGB为二面角A-MN-B的平面角.
∵点![]() ,点
,点![]() ,∴点
,∴点![]()
∴![]() ,
,![]() ,
,
∴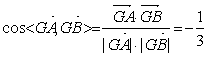 ,
,
∴故所求二面角![]() =
= ![]() -
-![]()
20.(Ⅰ)解:由题意,可设椭圆的方程为![]() .由已知得
.由已知得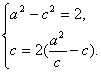 解得
解得![]() 所以椭圆的方程为
所以椭圆的方程为![]() ,离心率
,离心率![]() .(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为
.(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为![]() .由方程组
.由方程组
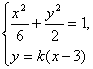 得
得![]() 依题意
依题意![]() ,得
,得![]() .设
.设![]() ,则
,则![]() , ①
, ①
![]() . ② 由直线PQ的方程得
. ② 由直线PQ的方程得![]() .于是
.于是
![]() . ③ ∵
. ③ ∵![]() ,∴
,∴![]() . ④. 由①②③④得
. ④. 由①②③④得![]() ,从而
,从而![]() .
.
所以直线PQ的方程为![]() 或
或![]() . (Ⅲ)证明:
. (Ⅲ)证明:![]() .由已知得方程组
.由已知得方程组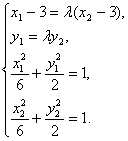
注意![]() ,解得
,解得![]() . 因
. 因![]() ,
,
故![]()
![]() .
.
而![]() ,所以
,所以![]() .
.