高二数学上学期期末复习训练(五)
出题人:广东省阳江市第一中学周如钢
(40分钟完成)(圆锥曲线方程单元)
一、选择题:(本大题共7小题,每小题7分,共49分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 请把答案填入后面指定的空格里.
1.已知![]() 的周长是16,
的周长是16,![]() ,B
,B![]() 则顶点C的轨迹方程是( )
则顶点C的轨迹方程是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.抛物线![]() 的焦点坐标是( )
的焦点坐标是( )
(A)(0,![]() )
(B)(
)
(B)(![]() ,0) (C)
(0,1) (D)(1,0)
,0) (C)
(0,1) (D)(1,0)
3.已知双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.椭圆![]() 的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在
的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在![]() 轴上,那么PF1是PF2的( )
轴上,那么PF1是PF2的( )
(A)7倍 (B)5倍 (C)4倍 (D)3倍
5.设椭圆![]() 和双曲线
和双曲线![]() 的公共焦点为
的公共焦点为![]() ,
,![]() 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos![]() 的值等于( )
的值等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.抛物线![]() 上的点到直线
上的点到直线![]() 距离的最小值是 ( )
距离的最小值是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.若动点P、Q是椭圆![]() 上的两点,O是其中心,若
上的两点,O是其中心,若![]() ,则中心O到PQ的距离OH必为( )
,则中心O到PQ的距离OH必为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题: 本大题共3小题,每小题7分,共21分,把答案填在题中横线上.
8.以![]() 的焦点为顶点,顶点为焦点的椭圆方程为
.
的焦点为顶点,顶点为焦点的椭圆方程为
.
9.直线y=x-1被双曲线2x2-y2=3所截得弦的中点坐标是______,弦长为______.
10.已知抛物线![]() ,过点
,过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]()
两点,则![]() 的最小值是
的最小值是
班别___________、学号______、姓名___________
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 答案 |
8.____________; 9.__________; 10.____________;
三、解答题: 本大题共两小题,每小题15分,共30分,解答应写出文字说明,证明过程或演算步骤.
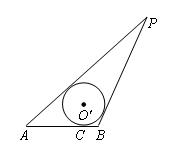
11.抛物线y2=4x与双曲线x2-y2=5相交于A、B两点,求以AB为直径的圆的方程.
12.如图,已知线段AB=4,动圆![]() 与线段AB切于点C,且AC-BC=2
与线段AB切于点C,且AC-BC=2![]() ,过点A,B分别作⊙
,过点A,B分别作⊙![]() 的切线,两切线相交于P,且P、
的切线,两切线相交于P,且P、![]() 均在AB的同侧.
均在AB的同侧.
⑴建立适当坐标系,当![]() 位置变化时,求动点P的轨迹E的方程;
位置变化时,求动点P的轨迹E的方程;
⑵过点B作直线![]() 交曲线E于点M、N,求△AMN的面积的最小值.
交曲线E于点M、N,求△AMN的面积的最小值.
高二数学上学期期末复习训练(五)答案(圆锥曲线方程单元)
BCAAB AC 8.![]() 9.(-1,-2),
9.(-1,-2),![]()
11.(x-5)2+y2=20
12.⑴以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标,并设点P坐标为P(x,y),设PA、PB分别切⊙![]() 于E、F,则PE=PF,AE=AC,BC=BF,∵PA-PB=AC-BC=2
于E、F,则PE=PF,AE=AC,BC=BF,∵PA-PB=AC-BC=2![]() ,
,
故点P 的轨迹为以A、B为焦点,实轴长为2![]() 的双曲线右支(除去与
的双曲线右支(除去与![]() 轴交点)
轴交点)
由题意,![]() 故P点轨迹E的方程为:
故P点轨迹E的方程为:![]()
⑵设直线l的倾斜角为q,直线l方程为y =tanq·(x-2)及x=2,注意到q≠0,
∴直线![]() 方程可写成y·cotq=x-2,由直线l与E交于M、N两点知
方程可写成y·cotq=x-2,由直线l与E交于M、N两点知![]()
由![]()
![]()
![]() 由y1-y22=
由y1-y22=![]() 得:
得:
S△AMN=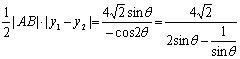 由
由![]() ,知
,知![]() ∵函数
∵函数![]() 在区间(0,-∞)上为增函数.∴
在区间(0,-∞)上为增函数.∴![]() ,即
,即![]() 时,(S△AMN)min=4
时,(S△AMN)min=4![]()