高二级数学单元检测题
——导数及其应用
班级：______________ 姓名：______________ 座号：______________ 评分：______________
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（每小题5分，共40分）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
1．下列函数中,在
上为增函数的是
A．
B．
C．
D．
2．
A．在（－∞，＋∞）单调增加
B．在（－∞，＋∞）单调减少
C．在（－1，1）单调减少，其余区间单调增加
D．在（－1，1）单调增加，其余区间单调减少
3．当x≠0时，有不等式
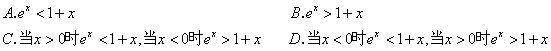
4．若连续函数在闭区间上有惟一的极大值和极小值，则
A．极大值一定是最大值，极小值一定是最小值
B．极大值必大于极小值
C．极大值一定是最大值，或极小值一定是最小值
D．极大值不一定是最大值，极小值也不一定是最小值
5．以下四图，都是同一坐标系中三次函数及其导函数的图像，其中一定不正确的序号是
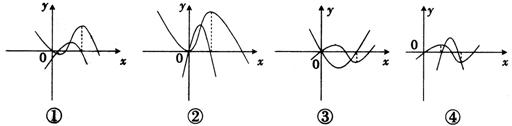
A．①、② B．①、③ C．③、④ D．①、④
6．下列求导运算正确的是
A．(x+
B．(log2x
=
C．(3x=3xlog3e
D．(x2cosx=－2xsinx
7．以正弦曲线y=sinx上一点P为切点的切线为直线l，则直线l的倾斜角的范围是
A．
∪
B．
C．
D．∪
8．
,
分别是定义在
上的奇函数和偶函数，当
时,
，
且
，则不等式
的解集是
A．(－3，0)∪(3，+∞) B．(－3，0)∪(0，3)
C．(－∞，－3)∪(3，+∞) D．(－∞，－3)∪(0，3)
二、填空题：请把答案填在题中横线上（每小题5分，共30分）．
9．以函数
为导数的函数图象过点（9，1），则函数
＝____________________．
10．在曲线
的切线中斜率最小的切线方程
是____________________. （图1）
11．如圆的半径以
12．已知
，奇函数
在
上单调，则字母
应满足的条件是__________．
13．函数y=f(x)定义在区间（-3，7）上，其导函数如图1所示，则函数y=f(x)在区间（-3，7）上极小值的个数是__________个．
14．已知函数
和
的图象在
处的切线互相平行，则
=__________．
三、解答题：解答应写出文字说明、证明过程或演算步骤（15、16题各12分，其余每题各14分，共80分）．
15．已知抛物线
与直线
（Ⅰ）求两曲线的交点；
（Ⅱ）求抛物线在交点处的切线方程．
16．已知函数
（Ⅰ）求的单调区间；
（Ⅱ）求
上的最值．
17．设
，当
时，
恒成立，求实数
的取值范围．
18．已知
且
，试用导数证明不等式：
．
19．（06年福建卷）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量
（升）关于行驶速度
（千米/小时）的函数解析式可以表示为：
．已知甲、乙两地相距100千米
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
20．（06年广东卷）设函数
分别在
、
处取得极小值、极大值．
平面上点A、B的坐标分别为
、
,该平面上动点P满足
,点Q是点P关于直线
的对称点．求：
（Ⅰ）点A、B的坐标；
（Ⅱ）动点Q的轨迹方程．
导数及其应用参考答案
一、1．B；2．C；3．B；4．D；5．C；6．B；7.A；8．D．
二、9．
；10．
；11． 40π cm2/s；12．
；13．2；14．6．
三、15．解：（1）由
，求得交点A（－2,0），B（3,5） （2）因为
，则
所以抛物线在A、B两点处的切线方程分别为
与
即
与
16．解：(I) 
令
得
若 
则
，
故在
上是增函数，在
上是增函数 
若 
则
，故在
上是减函数
(II) 
17．解：
，由
得
，即
或
；
由
得
即
，所以函数单调增区间是
，
；
函数的单调减区间是
。由
恒成立，
大于的最大值。当时，(1)当
时，为增函数，所以
；(2)当
时，为减函数，所以
；(3)当
时，为增函数，所以
；因为
，从而
18．分析：
证明：设
∵
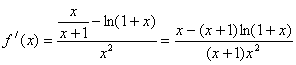
且
，∴
∴
∴
∴在
上单调递减
又∵
且
∴
即
∴
19．解：（I）当
时，汽车从甲地到乙地行驶了
小时，
要耗没
（升）。
答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油
（II）当速度为千米/小时时，汽车从甲地到乙地行驶了
小时，设耗油量为
升，
依题意得
令
得
当
时，
是减函数；
当
时，
是增函数。
当
时，取到极小值
因为在
上只有一个极值，所以它是最小值。
答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为
20．解：(I)令
解得
当
时,
, 当
时,
,当时,
所以,函数在
处取得极小值,在
取得极大值,故
,
所以, 点A、B的坐标为
.
(II)设
，
，
，所以
，又PQ的中点在
上，所以
消去
得